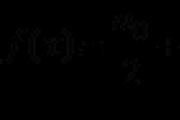Pravila i formule diferencijacije slične su funkcijama preklapanja. Funkcija preklapanja

Funkcije sklopivi izgled nije ga ispravno nazvati izrazom "sklopiva funkcija". Na primjer, izgleda još više pomireno, ali funkcija preklapanja nije, na vídmínu víd.

Na tsíy statti mi ćemo razumjeti s razumijevanje funkcija preklapanja, učeći prikazati íí̈ u skladištima elementarnih funkcija, dajemo formulu za poznavanje íí̈ sličnih i izvještajnih rješenja karakterističnih aplikacija.

U slučaju savršenih aplikacija, stalno pobjeđujemo tablicu sličnih i pravila razlikovanja, pa ih šišajte pred vašim očima.

funkcija preklapanja- Ovo je funkcija čiji je argument također funkcija.

Po našem mišljenju, svrha najrazumnije. Pametno, možete misliti na f(g(x)). Odnosno, g(x) kao argument funkcije f(g(x)) .

Na primjer, neka je f funkcija tangente luka, a g(x) = lnx je funkcija prirodnog logaritma, pa je funkcija savijanja f(g(x)) funkcija arctg(lnx). Još jedna stražnjica: f je funkcija povezivanja na četvrti korak, i - tsila racionalna funkcija (čudo), todi .

Na svoj način, g(x) može biti sklopiva funkcija. Na primjer, . Pametno se takav viraz može prepoznati kao . Ovdje je f funkcija sinusa, funkcija varijacije kvadratnog korijena, - Racionalna funkcija sačmarice. Logično je priznati da koraci ulaganja funkcija mogu biti kao završni prirodni broj.

Često možete jednostavno pozvati funkciju sastav funkcija.

Formula poznate funkcije preklapanja.

guzicom.

Upoznajte praktične funkcije sklapanja.

Riješenje.

U tom slučaju f je kvadratna funkcija, a g(x) = 2x+1 je linearna funkcija.

Os izvješća je rješenje s različitim formulama za sličnu funkciju preklapanja:

Hajde da znamo što ću učiniti, nakon što sam unaprijed pitao gledajući vanjske funkcije.

otzhe,

Poput bachita, rezultati zbígayutsya.

Pokušajte ne zalutati, kao funkcija ê f , već kao g(x) .

Objasnimo to s guzom za poštovanje.

guzicom.

Upoznajte se s praktičnim funkcijama sklapanja koje .

Riješenje.

U prvom slučaju, f je kvadratna funkcija, a g(x) je sinusna funkcija, dakle
.

U drugom pogledu, f je sinusna funkcija, a a funkcija stanja. Kasnije, za formulu, mogu biti dodatne funkcije preklapanja

Može se vidjeti formula slične funkcije

guzicom.

Razlikujte funkciju .

Riješenje.

Za koju funkciju preklapanja stražnjice možete mentalno zapisati kako , de - funkcija sinusa, funkcija veze na treći korak, funkcija logaritma na bazi e, funkcija uzimanja tangente luka i linearna funkcija drugog koraka.

Iza formule slične funkcije preklapanja

Sada znamo

Zajedno odabiremo oduzete međurezultate:

Nema ništa strašno, sredite funkcije preklapanja poput matrioške.

O čemu mogu završiti članak, yakby zhodne ale ...

Bazhano jasno razumije, ako postavite pravila diferencijacije i tablicu sličnih, i ako je formula slične funkcije preklapanja.

MOLIM VAS POSEBNO POŠTOVANJE. Razgovarajmo o uvođenju funkcija u kontekst funkcija preklapanja. Osim toga, sačuvat ćete svoju snagu, a bit ćete uspješni ako budete imali sreće.

Učimo iz jednostavnih aplikacija. funkcija možete vidjeti kako ga presavijam: g(x) = tgx , . Također, možete odmah zastosovuvat formula pokhídnoí̈ sklopiva funkcija

Funkcija osi ne može se nazvati sklopivim.

Ova funkcija je zbroj triju funkcija, 3tgx i 1. Hocha - ê sklopiva funkcija: - statička funkcija (kvadratna parabola), i f - tangentna funkcija. U tu svrhu stavljamo formulu sumi diferencijacije:

Izgubio sam znanje o sljedećim funkcijama preklapanja:

Tom.

Spodívaêmosya, scho ste uhvatili bit.

Da biste bili još nevjerojatniji, možete se pobrinuti da se funkcije preklapanja mogu uključiti u skladište funkcija preklapanja, a funkcije preklapanja mogu biti dijelovi za pohranu funkcija preklapanja.

Kako je kundak razvrstan za skladišne ​​dijelove funkcije .

Perche Ovo je sklopiva funkcija, kao što možete zamisliti, gdje je f logaritamska funkcija na bazi 3, a g(x) je zbroj dviju funkcija і . Tobto, .

Na drugačiji način, Pozabavimo se funkcijom h (x). pobijedio .

Zbroj dviju funkcija je , de - Funkcija preklapanja s brojčanim koeficijentom 3 . - funkcija povezivanja na kocku; - kosinusna funkcija; - linearna funkcija.

Tse zbroj dviju funkcija i , de - sklopiva funkcija, - eksponencijalna funkcija, - statička funkcija.

Na takav način,

treći, prohodan do , jak cijela ta racionalna funkcija

Funkcija kvadriranja, - funkcija logaritma na bazi e.

Otac,.

Predloženo:

p align="justify"> Sada je struktura funkcije shvaćena i postalo je jasno kako formule i u slijedu zastosovuvat na njeno razlikovanje.

Na različitim funkcijama diferencijacije (znakovi budućnosti) možete učiti iz varijacija sličnih zadataka.

Nakon prednje topničke pripreme bit će manje strašnih kundaka s 3-4-5 dodataka funkcija. Moguće je, ako zagazite dvije kundake, bit će kao preklapanje, ali ako ih shvatite (bilo da patite), onda će vam sve ostalo u diferencijalnoj računici dići djetinjastu groznicu.

guza 2

Znati povezane funkcije

Kako je zamišljeno, s potrebnom funkcijom preklapanja, mijenjat ćemo se, potrebno je pravo ROZIBRATISYA na umetcima. U mirnim situacijama, ako sumnjate, pogodit ću ispravan trik: uzmite zadnju vrijednost "iks", na primjer, i pokušajte (misli u crnom) staviti značenje u "strašan viraz".

1) Trebamo izbrojati viraz na leđima, onda je suma najveća investicija.

2) Zatim je potrebno izračunati logaritam:

4) Dodajmo kosinus kocki:

5) Na petoj najkraćoj cijeni:

6) Í, nareshti, sama stvarna funkcija je kvadratni korijen:

Formula diferencijacije funkcije preklapanja zastosovyvaetsya obrnutim redoslijedom, u obliku najvažnije funkcije, unutarnjoj. Mi vidimo:

Chebto bez pardona:

1) Pogledajte kvadratni korijen.

2) Vodite računa o maloprodajnom, zamjenskom pravilu

3) Pokhídna trojke su skuplje na nulu. Kod drugog dodana činimo korak (kocka).

4) Pogledajmo kosinus.

6) Ja, nareshti, bacim pogled na najveći depozit.

Možda je važnije, ali ipak nije najbolja životinjska guza. Uzmite, na primjer, odabir Kuznetsova i cijenit ćete svu ljepotu i jednostavnost odabranog izgleda. Sjetio sam se da ću voljeti nešto uspavati, razmisliti, što je učenik pametan, kao što znaš funkcije preklapanja, što nije pametno.

Uvredljiv primjer neovisnog rješenja.

guza 3

Znati povezane funkcije

Naputak: Pravilo linearnosti i pravilo diferencijacije stvaranja su leđa uz leđa

Izvana, rješenje je da je slično lekciji.

Došao je čas da prijeđemo na nešto kompaktnije i ljepše.
To nije rijetka situacija, jer kundak ima ne dvije, već tri funkcije. Kako znati je li rad tri množitelja dobar?

zadnjica 4

Znati povezane funkcije

Pitamo se malo, ali zašto se tri funkcije ne mogu pretvoriti u dvije funkcije? Na primjer, yakby smo imali dvije bogate artikulacije, tada je bilo moguće otvoriti lukove. Ali u aplikaciji su sve funkcije različite: koraci, eksponent i logaritam.

U takvim situacijama je potrebno sukcesivno zaustaviti pravilo diferencijacije stvaranja dvaput

Fokus je na činjenici da za "y" imamo bitno različite dvije funkcije: , a za "ve" - ​​logaritam: . Zašto možeš biti tako dosadan? Hiba - zašto ne dva višekratnika i pravilo ne funkcionira? Nema ništa sklopivo:

Sada odjednom izgubio pravilo nakloniti se:

Još uvijek možete biti ljuti i kriviti sebe za sljepoočnice, ali u ovoj situaciji bolje je izgubiti se u takvom izgledu - lakše se prevrnuti.

Pogledom se stražnjica može slomiti na drugi način:

Uvredljivi načini završetka su apsolutno jednaki.

guza 5

Znati povezane funkcije

Ovo je primjer samostalnog rješenja, prije svega, na prvi način.

Pogledajmo analogne aplikacije s razlomcima.

guza 6

Znati povezane funkcije

Ovdje možete ići na nekoliko načina:

Abo ovako:

Ali rješenje je da se zapiše kompaktnije, kao u prvom retku, da se pobijedi pravilo diferencijacije privatnog , Prihvaćam za cijeli broj:

Na principu, zadnjica je slomljena, a ako se u takvom pogledu lišite joge, onda nećete biti pomilovani. Ale, da bude očito, na sat vremena prevrni u crno, ali zašto ne možeš reći?

Donesimo brojke do zastave za spavanje i dobijmo trostruku površinu kadra:

Minus dodatnih pitanja je činjenica da pomilovanja neće biti dopuštena u vrijeme poznatih, već u banalnim školskim preobrazbama. S druge strane, vikladachi često odbijaju zadatak i traže da ga "dovedu na put" goreg.

Najjednostavniji primjer za neovisnu viziju:

guza 7

Znati povezane funkcije

Nastavljamo svladavati poznavanje poznatog i odmah možemo pogledati tipično odstupanje, ako je "strašni" logaritam propagiran za razlikovanje

Operacija vizualizacije naziva se diferencijacija.

Kao rezultat razvoja problema o razlici između najjednostavnijih (a ne najjednostavnijih) funkcija oznake najgore, kao i između poboljšanja argumenta, pojavila se tablica sličnih i točno definiranih pravila diferencijacije. Isaac Newton (1643.-1727.) i Gottfried Wilhelm Leibniz (1646.-1716.) bili su prvi u području znanja o prošlosti.

Stoga, u našem satu, da bismo znali postoje li funkcije, nije potrebno izračunati razliku između poboljšanja funkcije i poboljšanja argumenta, već je potrebno ubrzati tablicu sličnih s pravila diferencijacije. Za znanje o budućnosti treba koristiti uvredljiv algoritam.

Znati pokhidnu, potreban viraz pod znakom moždanog udara proširiti skladište jednostavnih funkcija ta vznachiti, yakami (tvir, zbroj, privatno) vezane uz ove funkcije. Dalí pokhídní elementarni funktsíy znachimo í u tablicama ín pokhídnih, i formule pokhídnih creativ, sum ta chasto - ín pravila diferencijacije. Tablica sličnih pravila za razlikovanje podataka nakon prve dvije aplikacije.

primjer 1. Znati povezane funkcije

Riješenje. Iz pravila diferencijacije jasno je da je zbroj funkcija isti kao i zbroj sličnih funkcija, tj.

Iz tablica sličnih je jasno da je "iksa" isto što i jednostruka, a sinus je kosinus. Zamijenite vrijednosti qi za zbroj pokhídnyh i znamo potrebnu mentalnu zadaću pokhídnua:

guza 2. Znati povezane funkcije

Riješenje. Drugačije, kao da ću izgubiti svoj zbroj, u nekom drugom dodatku s konstantnim množiteljem, mogu ga kriviti za predznak lošeg:

Dokle god se okrivljuje hrana, uzimaju se zvijezde, smrad u pravilu postaje jasniji nakon upoznavanja s tablicom sličnih i najjednostavnijim pravilima razlikovanja. Prije njih odmah prolazimo.

Tablica sličnih jednostavnih funkcija

1. Pokhídna konstante (brojevi). Bez obzira postoji li broj (1, 2, 5, 200 ...), takva će funkcija biti drugačija. Držite se do nule. Važnije je zapamtiti ono što je češće potrebno
2. Pokhídna nezalezhnaya zminnoy. Uglavnom "iksa". Zaboravite zdravu samoću. Tako je važno zapamtiti to dugo vremena
3. Pokhídna korak. Na nogama trešnje sata, potrebno je prepraviti ne-kvadratne korijene.
4. Pokhídna zminnoí̈ na koraku -1
5. Pokhídna kvadratni korijen
6. Pokhídna sinus
7. Pokhídna kosinus
8. Pokhídna tangenta
9. Pokhídna kotangens
10. Slično kao i arcsin
11. Slično kao i arkosinus
12. Pokhídna arktangent
13. Pokhídna lučna tangenta
14. Slično prirodnom logaritmu
15. Gruba logaritamska funkcija
16. Pokhídna eksponenti
17. Pokhidna funkcije prikaza

Pravila diferencijacije

1. Pokhídna sumi chi maloprodaja
2. Radite dobar posao
2a. Pokhídna virazi, pomnoženo s konstantnim množiteljem
3. Idi privatno
4. Funkcija preklapanja

Pravilo 1Koje funkcije

diferencijacija u trenutnoj točki, zatim u istoj točki diferencijacije i funkcije

zašto

tobto. sličan zbroj algebarskih funkcija sličan je zbroj algebara sličnih funkcija.

Posljedica. Kao dvije funkcije koje se razlikuju, obnavljaju na trajnom dodavanju, onda su slične, onda.

Pravilo 2Koje funkcije

diferencirane u trenutnoj točki, zatim u istoj točki, te dodatne točke se diferenciraju

zašto

tobto. rad dviju funkcija je dobar za zbroj rada kože s tim funkcijama za ostatak.

Zadnji 1. Za loš znak može se okriviti konstantni množitelj:

Posljednje 2. Pokhídna stvoriti dekilkoh funktsíy, scho differenziyuyutsya, dobrívnyuê tvoríví vídnoí̈ kohídnoí̈ derzhnoi z spívmníníkív ín sve ínshí.

Na primjer, za tri višekratnika:

Pravilo 3Koje funkcije

diferencijacije u deyakíy točki і , onda se na ovom mjestu diferencira i jau/v , štoviše

tobto. slično privatnom dvofunkcionalnom kadru, brojka tolike razlike tvorevina bannermana za mrtvog numeričara i brojčanika za transparenta, a bannerman je kvadrat velikog broja.

De sho šukati na druge strane

Kada znate dobre stvari, a često i u stvarnim glavama, potrebno je zastosovuvati mnoga pravila razlikovanja, tako da ima više aplikacija za dobre stvari - u statistici"Stvorite vlastite privatne funkcije".

Poštovanje. Slid da ne zbuni konstantu (taj broj) kao dodatak zbroju i kao konstantni množitelj! Za vipadiana, dodanka í̈í̈ pokhídna je skuplja na nulu, a za vrijeme brzog množitelja bit će okrivljena za znak pokhídnyh. Ovo je tipično oproštenje, kako se to vidi na stadiju oplemenjivanja prošlosti, ali u svijetu se već vidi koliko je jedno-dva kata srednji učenik tsyu pardon više ne pljačkaju.

A što se tiče diferencijacije stvaranja privatnog, imate dodatak u"v, u kojem u- broj, na primjer, 2 ili 5, to je konstanta, tada će isti broj biti jednak nuli i, zatim će svi dodaci biti jednaki nuli (takav obrazac uređenja za stražnjicu 10).

Insha često oproštenje- mehaničko rješenje ležerne funkcije preklapanja kao ležerne jednostavne funkcije. Tom sklopive funkcije posvećen okrem statutu. Ale, leđa uz leđa, znam bolje jednostavne funkcije.

Usput ne možete bez promjene viraza. Za koga će vam možda trebati pomoć iz novih prozora Díí zí koraci i korijeniі Díí̈ s razlomcima .

Kako pronaći rješenja za slične razlomke s koracima i korijenima, pa ako funkcija može pogledati , a zatim slijedi lekcija "Dobro je imati vreću snimaka sa koracima i korijenjem."

Yakshcho dobro prije nego što zavdannya nachebto , onda ste zauzeti "Vyrobní jednostavnim trigonometrijskim funkcijama".

Pokrokovi kundaci - kako znati hoću li

primjer 3. Znati povezane funkcije

Riješenje. Očito je da dio virusaze funkcionira: cijela virusaza predstavlja tvir, kao i množitelji - sumi, druga ima jedan dodatni množitelj. Postoji fiksno pravilo diferencijacije za stvaranje: stvorite dvije funkcije ljepše, zbroj kreacija kože i ove funkcije za ostalo:

Dali smo stabilno pravilo diferencijacije zbroja: zbroj algebarskih funkcija sličan je zbroju algebre sličnih funkcija. Naš um u kožnoj vrećici ima još jedan dodatak sa znakom minus. U zbroju kože postoji mnogo neovisnih promjena, ona je kao zdrava, i konstanta (broj) koja je kao nula. Otzhe, "iks" kod nas se pretvara u jedan, a minus 5 - na nulu. U drugom slučaju, "iks" se množi s 2, pa se dva množi s istim, kao "iks" je nestao. Oduzimamo sljedeće vrijednosti:

Zamislimo da je zbroj kreativaca pronašao potrebne potrebe uma za sve funkcije:

I moguće je preokrenuti razvoj zadataka za budućnost.

zadnjica 4. Znati povezane funkcije

Riješenje. Neophodno je da znamo tajnu privatnog. Zastosovuêmo formula diferentiyuvannya chastki: pokhídna chastki dvoh funktsíy dorívnyuê razlomak, broj takve razlike kreacija zastave za smrt broja i broja za smrt zastave, a zastava je kvadrat broja brojčani. Uzimamo:

Već smo znali u stražnjici 2. Ne zaboravimo da je istina, da je drugi sp_multiplier u knjizi brojeva u stringu uzet sa znakom minus:

Kako gledate na svestranost takvih zadataka, u kojima trebate znati točne funkcije, de sucile akumulaciju korijena tih koraka, kao npr. , onda ljubazno zamolite za posao "Virobna sumi snimci sa koracima i korijenjem" .

Pa, morate znati više o lošijim sinusima, kosinusima, tangentima i ostalima trigonometrijske funkcije, onda, ako funkcija može pogledati , onda imate lekciju "Kompletne jednostavne trigonometrijske funkcije" .

Primjer 5. Znati povezane funkcije

Riješenje. Ova funkcija ima bachimo tver, jedan od zajedničkih množitelja njih je kvadratni korijen nezavisne promjene, sa sličnim smo upoznali iz tablica sličnih. Iza pravila diferencijacije uzima se stvaranje te tablične vrijednosti sličnog kvadratnog korijena:

Moguće je ponovno razmotriti rješenje zadataka za budućnost na online kalkulatori .

Primjer 6. Znati povezane funkcije

Riješenje. Ova funkcija je privatnija, udaljenost bilo koje je kvadratni korijen neovisne promjene. Iza pravila razlikovanja privatnog, kako smo ga ponovili i stavili u aplikaciju 4, uzima se ta tablična vrijednost sličnog kvadratnog korijena:

Da bismo uzeli razlomak u knjizi brojeva, pomnožimo knjigu brojeva i natpis.

Funkcije preklapanja izgledaju kao uobičajeno za određenu funkciju preklapanja. Ako je to funkcija oblika y \u003d sin x - (2 - 3) a r c t g x x 5 7 x 10 - 17 x 3 + x - 11, tada se njeno ne može sklopiti u prikaz y \u003d sin 2 x.

Ovaj će članak pokazati razumijevanje funkcije preklapanja i manifestacije. Ispravak s formulama o značenju sličnog od kundaka rješenja do visnovke. Zastosuvannya tablice lošijeg i pravila diferencijacije zamjetno mijenjaju sat za promjenu lošijeg.

Glavni termini

Imenovanje 1

Funkcija koja se može sklopiti razmatra takvu funkciju, kao što je argument također funkcija.

Označava se na sljedeći način: f (g (x)) . Moguće je da se funkcija g(x) uzima u obzir argumentom f(g(x)).

Imenovanje 2

Isto tako, funkcija f i ê su funkcija kotangensa, tada je g(x) = ln x funkcija prirodnog logaritma. Imajte na umu da se sklopiva funkcija f(g(x)) može napisati kao arctg(lnx). Inače, funkcija f, koja je funkcija od 4 koraka, de g (x) \u003d x 2 + 2 x - 3 uzima se u obzir cijelom racionalnom funkcijom, pretpostavlja se da je f (g (x)) \ u003d (x 2 + 2 x - 3) 4 .

Očito je da g(x) može biti sklopiv. Iz stražnjice y \u003d sin 2 x + 1 x 3 - 5 jasno je da vrijednost g može kubični korijen s razlomkom. Danski viraz može se označiti kao y \u003d f (f 1 (f 2 (x))). Zvijezde mogu biti da je f funkcija sinusa, a f 1 je funkcija koja se širi ispod kvadratnog korijena, f 2 (x) \u003d 2 x + 1 x 3 - 5 je frakcijska racionalna funkcija.

Imenovanje 3

Stopa doprinosa je dodijeljena kao neki prirodni broj i zapisuje se kao y = f (f 1 (f 2 (f 3 (... (f n (x))))))))).

Imenovanje 4

Razumijevanje sastava funkcije ovisi o broju ulaznih funkcija za mentalni zadatak. Za savršenstvo pobjednosti, formula za sličnost sklopive funkcije uma

(f(g(x))) "=f"(g(x)) g"(x)

Prijavite se

guza 1

Nađi funkciju preklapanja oblika y = (2 x + 1) 2 .

Riješenje

Iza uma se može vidjeti da je f kvadratna funkcija, a g (x) \u003d 2 x + 1 uzima se u obzir linearnom funkcijom.

Napravimo sličnu formulu za funkciju preklapanja i zapišimo je:

f "(g(x)) = ((g(x)) 2)" = 2 (g(x)) 2 - 1 = 2 g(x) = 2 (2x + 1); g "(x) = (2 x + 1)" = (2 x) "+ 1" = 2 x " + 0 = 2 1 x 1 - 1 = 2 ⇒ (f (g (x))) "=f "(g(x)) g"(x) = 2 (2x + 1) 2 = 8x + 4

Potrebno je znati kako pojednostaviti funkciju vanjskog izgleda. Uzimamo:

y = (2x + 1) 2 = 4x2 + 4x + 1

Zvídsi maêmo, scho

y"=(4x2+4x+1)"=(4x2)"+(4x)"+1"=4(x2)"+4(x)"+0==4 2 x 2 - 1 + 4 1 x 1 - 1 = 8 x + 4

Rezultati su bili iskrivljeni.

Prilikom izvršavanja zadatka ove vrste, važno je razumjeti, de-roztashovuvatimeet funkciju oblika f í g (x) .

guza 2

Trebali biste znati sljedeće funkcije savijanja oblika y = sin 2 x i y = sin x 2.

Riješenje

Prvi unos funkcije mora odgovarati da je f kvadratna funkcija, a g (x) sinusna funkcija. Todi otrimaemo to

y "= (sin 2 x)" = 2 sin 2 - 1 x (sin x)" = 2 sin x cos x

Druga oznaka pokazuje da je f sinusna funkcija, a g(x) = x 2 ima smisla državna funkcija. Zvuči kao da će dodatna sklopiva funkcija biti napisana kao

y " \u003d (sin x 2) " \u003d cos (x 2) (x 2) " \u003d cos (x 2) 2 x 2 - 1 = 2 x cos (x 2)

Formula za slučajni y \u003d f (f 1 (f 2 (f 3 (. . (fn (x)))))) napisana je kao y "= f" (f 1 (f 2 (f 3 (. . .) fn (x)))))) f 1 "(f 2 (f 3 (. . (fn (x)))))) f 2 " (f 3 (. . . (fn ( x))) )). . . f n "(x)

guza 3

Pronađite sličnu funkciju y = sin (ln 3 a r c t g (2 x)).

Riješenje

Danska stražnjica prikazuje preklapanje ploče i oznaku proširenja funkcija. Tada je y \u003d f (f 1 (f 2 (f 3 (f 4 (x)))))) značajan, de f, f 1, f 2, f 3, f 4 (x) 3 koraka, funkcija s logaritmom i bazom e, funkcijom tangente luka i linearnom.

3 formule za označavanje sklopive funkcije

y "= f "(f 1 (f 2 (f 3 (f 4 (x))))) f 1 "(f 2 (f 3 (f 4 (x))))) f 2 "( f 3 ( f 4 (x))) f 3 "(f 4 (x)) f 4 "(x)

Uzimamo ono što trebamo znati

1. f "(f 1 (f 2 (f 3 (f 4 (x))))) = cos (ln 3 arctg (2x)).
2. f 1 "(f 2 (f 3 (f 4 (x)))) (2 x) = 3 ln 2 arctg (2 x) .
3. f 2 "(f 3 (f 4 (x))) je slično logaritamsko, onda je f 2 "(f 3 (f 4 (x))) = 1 a r c t g (2 x) .
4. f 3 "(f 4 (x)) kao sličan luk tangente, zatim f 3 "(f 4 (x)) \u003d 1 1 + (2 x) 2 = 1 1 + 4 x 2.
5. Uz značajan f 4 (x) = 2 x, postoji krivnja 2 za znak slične statičke funkcije s pokazateljem koji je dobar 1, zatim f 4 "(x) = (2 x)" = 2 x " \u003d 2 1 x 1 - 1 = 2.

Provodimo sažetak međurezultata i to uzimamo u obzir

y "= f "(f 1 (f 2 (f 3 (f 4 (x))))) f 1 "(f 2 (f 3 (f 4 (x))))) f 2 "( f 3 ( f 4 (x))) f 3 "(f 4 (x)) f 4 "(x) = = cos (ln 3 arktan (2 x)) 3 ln 2 arktan (2 x) 1 arktan (2 x) 1 1 + 4 x 2 2 = = 6 cos (ln 3 arktan (2 x)) ln 2 arktan (2 x) arktan (2 x) (1 + 4 x 2 )

Analiza takvih funkcija napravit će matrioške. Pravila diferencijacije ne mogu uvijek biti fiksirana očito za pomoć tablica gorih. Najčešće je potrebno zapisati formulu za značaj sličnih funkcija preklapanja.

Ísnuyut deyakí vídminností sklopivi tip sklopivih funkcija. Uz jasno razumijevanje razlika, posebno je lako prepoznati one kasnije.

zadnjica 4

Potrebno je sagledati nišanjenje takvog kundaka. Ako je to funkcija oblika y \u003d t g 2 x + 3 t g x + 1, tada se može vidjeti kao sklopivi oblik g (x) = t g x, f (g) = g 2 + 3 g + 1 . Očito je da je potrebno sastaviti formule za preklopnu formulu:

f "(g (x)) = (g 2 (x) + 3 g (x) + 1)" = (g 2 (x)) "+ (3 g (x))" + 1 " == 2 g 2 - 1 (x) + 3 g "(x) + 0 = 2 g (x) + 3 1 g 1 - 1 (x) \u003d \u003d 2 g (x) + 3 \u003d 2 tgx + 3; g " (x) = (tgx) " = 1 cos 2 x ⇒ y " = (f (g (x))) " = f " (g (x)) g " (x) = (2 tgx + 3 ) 1 cos 2 x = 2 tanx + 3 cos 2 x

Funkcija oblika y = t g x 2 + 3 t g x + 1 ne smatra se sklopivom; Međutim, t g x 2 se smatra preklopnom funkcijom, tada je statička funkcija oblika g (x) = x 2 í f tangentna funkcija. Za koga se treba razlikovati po torbi. Mi to prihvaćamo

y " = (tgx 2 + 3 tgx + 1) " = (tgx 2) " + (3 tgx) " + 1 " == (tgx 2) " + 3 (tgx) " + 0 = (tgx 2) " + 3 jer 2 x

Idemo na vrijednost slične funkcije preklapanja (t g x 2) ":

f "(g (x)) \u003d (tg (g (x)))" \u003d 1 cos 2 g (x) \u003d 1 cos 2 (x 2) g "(x) \u003d (x 2)" \u003d 2 x 2 - 1 \u003d 2 x ⇒ (tgx 2) "= f "(g (x)) g "(x) \u003d 2 x cos 2 (x 2)

Uzimamo da je y "= (t g x 2 + 3 t g x + 1)" = (t g x 2) "+ 3 cos 2 x = 2 x cos 2 (x 2) + 3 cos 2 x

Funkcije preklapanja mogu se uključiti prije funkcija preklapanja, a same funkcije preklapanja mogu biti funkcije preklapanja skladišta.

guza 5

Na primjer, pogledajmo sklopivu funkciju oblika y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x (x 2 + 1)

Ova funkcija se može predstaviti kao y = f (g (x)) , gdje je vrijednost f funkcija logaritma na bazi 3, a g (x) se uzima kao zbroj dviju funkcija oblika h ( x) = x 2 + 3 cos 3 (2 x + 1) + 7 ex 2 + 3 3 i k(x) = ln 2 x (x 2 + 1) . Očito, y = f(h(x) + k(x)) .

Pogledajmo funkciju h(x) . Cijena l (x) \u003d x 2 + 3 cos 3 (2 x + 1) + 7 do m (x) \u003d e x 2 + 3 3

Možda l(x) \u003d x 2 + 3 cos 2 (2 x + 1) + 7 \u003d n (x) + p (x) - zbroj dviju funkcija n (x) \u003d x 2 + 7 i p (x) \u003d 3 cos 3 (2 x + 1) , de p (x) \u003d 3 p 1 (p 2 (p 3 (x))) je funkcija preklapanja s numeričkim koeficijentom 3, a p 1 je funkcija kocke, p 2 kosinusna funkcija, p 3 (x) = 2 x + 1 - linearna funkcija.

Oduzeli smo da je m (x) = ex 2 + 3 3 = q (x) + r (x) - zbroj dviju funkcija q (x) = ex 2 í r (x) = 3 3 de q (x) = q 1 (q 2 (x)) je sklopiva funkcija, q 1 je funkcija s eksponentom, q 2 (x) = x 2 je funkcija stanja.

Može se vidjeti da je h (x) = l (x) m (x) = n (x) + p (x) q (x) + r (x) = n (x) + 3 p 1 (p 2 ( p 3 (x))) q 1 (q 2 (x)) + r (x)

Kada se prijeđe na pogled oblika k(x) = ln 2 x (x 2 + 1) = s (x) t (x), jasno je da je funkcija predstavljena u obliku preklapanja s(x) = ln 2 x = s 1 ( s 2 (x)) s racionalnim brojem t (x) = x 2 + 1, de s 1 ê kvadratna funkcija, i s 2 (x) = ln x - logaritamska s bazom e .

Čini se da ću vidjeti k (x) = s (x) t (x) = s 1 (s 2 (x)) t (x) .

Todi otrimaemo to

y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 ex 2 + 3 3 + ln 2 x (x 2 + 1) = = fn (x) + 3 p 1 (p 2 (p 3 ( x))) q 1 (q 2 (x)) = r (x) + s 1 (s 2 (x)) t (x)

Iza struktura funkcije postalo je jasno kako i kako formule trebaju biti fiksirane da bi se pojednostavio izraz za diferencijaciju. Da bismo poznavali takve zadatke i razumjeli ih, potrebno je vratiti se na točku diferencijacije funkcije, što je važno.

Kao da ste se sjetili oprosta u tekstu, budite ljubazni, pogledajte ga i pritisnite Ctrl + Enter

Prvi teorem o sklopivoj funkciji, koji je formuliran na sljedeći način:

Idemo 1) funkcija $u=\varphi (x)$ može imati $u_(x)"=\varphi"(x_0)$ u prvoj točki $x_0$; 2) funkcija $y=f(u)$ može promijeniti $y_(u)"=f"(u)$ za najnovije točke $u_0=\varphi (x_0)$. Slično, sklopiva funkcija $y=f\left(\varphi (x) \right)$ u točki pogađanja je također slična, jednaka dodatnoj obradi sličnih funkcija $f(u)$ i $\varphi (x) $:

$$ \left(f(\varphi (x))\right)"=f_(u)"\left(\varphi (x_0) \desno)\cdot \varphi"(x_0) $$

inače, za veću skraćenicu: $y_(x)"=y_(u)"\cdot u_(x)"$.

U stražnjem dijelu koje sam podijelio sve funkcije mogu izgledati $y=f(x)$ (zato možemo vidjeti samo funkcije jedne promjene $x$). Očito, u svim dionicama, pogrešno je uzeti $y"$ za promjenu $x$. Na primjer, oni koji su dobri za promjenu $x$ često zamjenjuju $y"$ s $y"_x$.

Na kundacima br. 1, br. 2 i br. 3 napravljen je izvještaj o procesu razumijevanja funkcija preklapanja. Butt br. 4 imenovanja za veće razumijevanje tablica potonjeg i može biti razumno.

Bazhano nakon ugradnje materijala u kundake br. 1-3, prijeđite na neovisno rješenje za kundake br. 5, br. 6 i br. Primijenite br. 5, br. 6 i br. 7 da donesete kratku odluku, tako da čitatelj može odmah provjeriti točnost svog rezultata.

Guzica #1

Pronađite sličnu funkciju $y=e^(\cos x)$.

Moramo znati točnu funkciju savijanja $y"$. Ako je $y=e^(\cos x)$, tada je $y"=\left(e^(\cos x)\right)"$. Da bismo znali trik $ \ left(e^(\cos x)\right)"$ osvoji formulu br. 6 iz tablica sličnih . Da bismo dobili formulu #6, potrebno je ispraviti ono što je po našem mišljenju $u=\cos x$. Nadalje, odluka se primjenjuje na banalne trafostanice formule br. 6 kako bi se $\cos x$ umjesto $u$:

$$ y"=\lijevo(e^(\cos x) \desno)"=e^(\cos x)\cdot (\cos x)" \tag (1.1)$$

Sada je potrebno znati vrijednost $(\cos x)"$. Vratimo se na donje tablice, birajući iz nje formulu br. 10. Zamjena $u=x$ za formulu br. 10, možda: $( \cos x)"=-\ sin x\cdot x"$. Sada nastavimo s jednakošću (1.1), dodajući je, nalazimo rezultat:

$$ y"=\left(e^(\cos x) \right)"=e^(\cos x)\cdot (\cos x)"= e^(\cos x)\cdot (-\sin x \cdot x") \oznaka (1.2) $$

Skílki $x"=1$, onda možemo nastaviti jednakost (1.2):

$$ y"=\left(e^(\cos x) \right)"=e^(\cos x)\cdot (\cos x)"= e^(\cos x)\cdot (-\sin x \cdot x")=e^(\cos x)\cdot (-\sin x\cdot 1)=-\sin x\cdot e^(\cos x) \tag (1.3) $$

Također, iz pariteta (1.3) može biti: $y"=-\sin x\cdot e^(\cos x)$. 1.3) Kasnije je pronađena slična sklopiva funkcija;

Vidpovid: $y"=-\sin x\cdot e^(\cos x)$.

Guzica #2

Pronađite sljedeće funkcije $y=9\cdot \arctg^(12)(4\cdot \ln x)$.

Moramo izračunati trošak $y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"$. Značajno je da se konstanta (to je broj 9) može kriviti za loš znak:

$$ y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"=9\cdot\left(\arctg^(12)(4\cdot \ln x) \desno)" \oznaka (2.1) $$

Sada prijeđimo na virazu $\left(\arctg^(12)(4\cdot \ln x) \right)"$. Da biste odabrali formulu iz tablica sličnih, lakše je, ja ću predstaviti virase, koja izgleda ovako: $\ left( \left(\arctg(4\cdot \ln x) \right)^(12)\right)"$. Sada je jasno da je potrebno osvojiti formulu broj 2, tobto. $\left(u^\alpha \right)"=\alpha\cdot u^(\alpha-1)\cdot u"$. Za qiu, formula se može predstaviti s $u=\arctg(4\cdot \ln x)$ i $\alpha=12$:

Dopuna jednakosti (2.1) oduzima se od rezultata, možda:

$$ y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"=9\cdot\left(\arctg^(12)(4\cdot \ln x) \right)"= 108\cdot\left(\arctg(4\cdot \ln x) \right)^(11)\cdot (\arctg(4\cdot \ln x))" \tag (2.2) $$

U ovoj situaciji, oprost je često dopušten, ako je prvi izbor formula $(\arctg \; u)"=\frac(1)(1+u^2)\cdot u"$ zamijeni formulu $\left( u^\ alpha \desno)"=\alpha\cdot u^(\alpha-1)\cdot u"$. S desne strane, prva stvar je kriva, ali pokhídna zvníshnyoí̈ funkcijeíí̈. Da biste razumjeli, kako će sama funkcija biti naziv izraza $\arctg^(12)(4\cdot 5^x)$, pokažite da poštujete vrijednost izraza $\arctg^(12)(4\ cdot 5^x)$ za bilo koju vrijednost od $x$. Počnite pogađanjem vrijednosti $5^x$, a zatim pomnožite rezultat s 4, oduzimajući $4\cdot 5^x$. Sada, s obzirom na rezultat, uzimamo arktangent, oduzimajući $arctg(4cdot 5^x)$. Zatim uzimamo broj u dvanaest koraka, oduzimajući $ arctg (12) (4 cdot 5 x) $. Kloni se, - tobto. zvedennya u koracima 12 - i bit će ista funkcija. I već sljedeće je bilo započeti odbijanje, koje je razbijeno ekvivalentnošću (2.2).

Sada je potrebno znati $(\arctg(4\cdot \ln x))"$. Formulu br. 19 od sličnih tablica možemo dobiti, zamjenjujući u nju $u=4\cdot \ln x$:

$$ (\arctg(4\cdot \ln x))"=\frac(1)(1+(4\cdot \ln x)^2)\cdot (4\cdot \ln x)" $$

Trohovi se mogu lako oduzeti od viraza, vrahovoyuchi $(4\cdot \nn x)^2=4^2\cdot (\ln x)^2=16\cdot \ln^2 x$.

$$ (\arctg(4\cdot \ln x))"=\frac(1)(1+(4\cdot \ln x)^2)\cdot (4\cdot \ln x)"=\frac( 1)(1+16\cdot \ln^2 x)\cdot (4\cdot \ln x)" $$

Jednakost (2.2) će sada postati ovako:

$$ y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"=9\cdot\left(\arctg^(12)(4\cdot \ln x) \desno)"=\\ =108\cdot\left(\arctg(4\cdot \ln x) \desno)^(11)\cdot (\arctg(4\cdot \ln x))"=108\cdot \left(\arctg(4\cdot \ln x) \right)^(11)\cdot \frac(1)(1+16\cdot \ln^2 x)\cdot (4\cdot \ln x)" \oznaka (2.3) $$

Više nije dovoljno znati $(4\cdot \ln x)"$. Za loš znak krivimo konstantu (to jest 4): $(4\cdot \ln x)"=4\cdot (\ln x)"$. da biste znali $(\ln x)"$ osvojite formulu #8 zamjenom $u=x$ u njoj: $(\ln x)"=\frac(1)(x)\cdot x"$. Ako je $x"=1$, tada je $(\ln x)"=\frac(1)(x)\cdot x"=\frac(1)(x)\cdot 1=\frac(1)(x) $. Nakon što smo oduzeli rezultat iz formule (2.3), oduzimamo:

$$ y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"=9\cdot\left(\arctg^(12)(4\cdot \ln x) \desno)"=\\ =108\cdot\left(\arctg(4\cdot \ln x) \desno)^(11)\cdot (\arctg(4\cdot \ln x))"=108\cdot \left(\arctg(4\cdot \ln x) \right)^(11)\cdot \frac(1)(1+16\cdot \ln^2 x)\cdot (4\cdot \ln x)" =\\ =108\cdot \left(\arctg(4\cdot \ln x) \right)^(11)\cdot \frac(1)(1+16\cdot \ln^2 x)\cdot 4\ cdot \frac(1)(x)=432\cdot \frac(\arctg^(11)(4\cdot \ln x))(x\cdot (1+16\cdot \ln^2 x)).$

Pretpostavljam da se funkcije preklapanja najčešće nalaze u jednom redu - kako piše u ostatku jednakosti. Stoga, prilikom izrade tipičnih rozrahunkív ili kontrolnih robota, rješenje nije obvezno sastaviti tako detaljno.

Vidpovid: $y"=432\cdot \frac(\arctg^(11)(4\cdot \ln x))(x\cdot (1+16\cdot \ln^2 x))$.

Guzica #3

Upoznajte $y"$ funkcije $y=\sqrt(\sin^3(5\cdot9^x))$.

Za cob troch, mijenjamo funkciju $y$ dodavanjem radikala (korijena) u istom koraku: $y=\sqrt(\sin^3(5\cdot9^x))=\left(\sin(5\) cdot 9^x) \desno)^(\frac(3)(7))$. A sada prijeđimo na loše stvari. $y=\lijevo(\sin(5\cdot 9^x)\desno)^(\frac(3)(7))$, tada:

$$ y"=\left(\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))\right)" \tag (3.1) $$

Osvajajući formulu br. 2 iz tablica sličnih, zamjenjujući u njoj $u=\sin(5\cdot 9^x)$ i $\alpha=\frac(3)(7)$:

$$ \left(\left(\sin(5\cdot 9^x)\desno)^(\frac(3)(7))\right)"= \frac(3)(7)\cdot \left( \sin(5\cdot 9^x)\desno)^(\frac(3)(7)-1) (\sin(5\cdot 9^x))"=\frac(3)(7)\cdot \lijevo(\sin(5\cdot 9^x)\desno)^(-\frac(4)(7)) (\sin(5\cdot 9^x))" $$

Prodovzhimo rivnist (3.1), vikoristuyuchi oduzimajući rezultat:

$$ y"=\left(\left(\sin(5\cdot 9^x)\desno)^(\frac(3)(7))\right)"=\frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\desno)^(-\frac(4)(7)) (\sin(5\cdot 9^x))" \tag (3.2) $$

Sada je potrebno znati $(\sin(5\cdot 9^x))"$. Formulu br. 9 moguće je dobiti iz tablica sličnih zamjenom $u=5\cdot 9^x$ u tome:

$$ (\sin(5\cdot 9^x))"=\cos(5\cdot 9^x)\cdot(5\cdot 9^x)" $$

Dodavanjem jednakosti (3.2) rezultatu možemo:

$$ y"=\left(\left(\sin(5\cdot 9^x)\desno)^(\frac(3)(7))\right)"=\frac(3)(7)\cdot \lijevo(\sin(5\cdot 9^x)\desno)^(-\frac(4)(7)) (\sin(5\cdot 9^x))"=\\ =\frac(3) (7)\cdot \left(\sin(5\cdot 9^x)\desno)^(-\frac(4)(7)) \cos(5\cdot 9^x)\cdot(5\cdot 9 ^x)" \oznaka (3.3) $$

Zaboravio sam znati $(5\cdot 9^x)"$. Za klip krivimo konstantu (broj $5$) za predznak sličnog, a zatim $(5\cdot 9^x)"=5\cdot (9^x) "$. Za vrijednost sličnog $(9^x)"$, kreirat ćemo formulu br. 5 od tablica sličnih, zamjenjujući $a=9$ i $u=x$ prije njega: $(9^x)"=9^x\cdot \ ln9\cdot x"$. Ako je $x"=1$, tada je $(9^x)"=9^x\cdot \ln9\cdot x"=9^x\cdot \ln9$. Sada možemo nastaviti s jednakošću (3.3):

$$ y"=\left(\left(\sin(5\cdot 9^x)\desno)^(\frac(3)(7))\right)"=\frac(3)(7)\cdot \lijevo(\sin(5\cdot 9^x)\desno)^(-\frac(4)(7)) (\sin(5\cdot 9^x))"=\\ =\frac(3) (7)\cdot \left(\sin(5\cdot 9^x)\desno)^(-\frac(4)(7)) \cos(5\cdot 9^x)\cdot(5\cdot 9 ^x)"= \frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) \cos(5\cdot 9 ^x)\cdot 5\cdot 9^x\cdot \ln9=\\ =\frac(15\cdot \ln 9)(7)\cdot \left(\sin(5\cdot 9^x)\desno) ^(-\frac(4)(7))\cdot \cos(5\cdot 9^x)\cdot 9^x. $$

Možete ponovno okrenuti korake na radikale (to je korijen) tako što ćete napisati $\left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7))$ izgledajući $\frac( 1 )(\left(\sin(5\cdot 9^x)\desno)^(\frac(4)(7)))=\frac(1)(\sqrt(\sin^4(5\) cdot 9 ^x)))$. Tada će biti napisano u ovom obliku:

$$ y"=\frac(15\cdot \ln 9)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7))\cdot \cos(5\cdot 9^x)\cdot 9^x= \frac(15\cdot \ln 9)(7)\cdot \frac(\cos (5\cdot 9^x)\cdot 9^x) (\sqrt(\sin^4(5\cdot 9^x))).$$

Vidpovid: $y"=\frac(15\cdot \ln 9)(7)\cdot \frac(\cos (5\cdot 9^x)\cdot 9^x)(\sqrt(\sin^4(5\) ) cdot 9^x)))$.

Guzica #4

Pokažite da su formule br. 3 i br. 4 u tablicama slične i posljednje formule br. 2 tablica.

Formula br. 2 iz tablica u nastavku ima sličnu funkciju $u^\alpha$. Zamjenom $\alpha=-1$ za formulu br. 2, uzimamo:

$$(u^(-1))"=-1\cdot u^(-1-1)\cdot u"=-u^(-2)\cdot u"\tag (4.1)$$

Ako je $u^(-1)=\frac(1)(u)$ i $u^(-2)=\frac(1)(u^2)$, tada se jednakost (4.1) može prepisati na sljedeći način: $ \ lijevo(\frac(1)(u) \right)"=-\frac(1)(u^2)\cdot u"$. Tse i ê formula br. 3 tablice sličnih.

Ja sam znovnemosya do formule br. 2 tablice gore. Zamislimo do $\alpha=\frac(1)(2)$:

$$\left(u^(\frac(1)(2))\right)"=\frac(1)(2)\cdot u^(\frac(1)(2)-1)\cdot u" =\frac(1)(2)u^(-\frac(1)(2))\cdot u"\tag (4.2) $$

Skílki $u^(\frac(1)(2))=\sqrt(u)$ i $u^(-\frac(1)(2))=\frac(1)(u^(\frac( 1) )(2)))=\frac(1)(\sqrt(u))$, tada se jednakost (4.2) može prepisati na sljedeći način:

$$ (\sqrt(u))"=\frac(1)(2)\cdot \frac(1)(\sqrt(u))\cdot u"=\frac(1)(2\sqrt(u) )\cdot u" $$

Otrimanova jednakost $(sqrt(u))"=\frac(1)(2sqrt(u))cdot u"$ i ê formula br. 4 tablica sličnih. Kao i Bachite, formule br. 3 i br. 4 tablica slične su formulama br. 2 sa zamjenom slične vrijednosti $ alfa $.