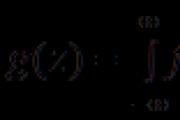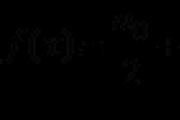Tekst rada je postavljen bez slike formula.
Nova verzija roboti je dostupan na kartici "Files roboti" u PDF formatu

"Tezh me, Newtonov binom!»

iz romana "Majstor i Margarita"

„Paskalov trikutnik je toliko jednostavan da možete zapisati decimalno dete. Upravo u tom času morat ćete se sakriti u vlastito nevidljivo blago i kupovat ćete još raznih aspekata matematike, kao da na prvi pogled možda nemate šta da spavate sami sa sobom. Takvi nepodijeljeni autoriteti dopuštaju korištenje Pascalovog trikutnika s jednom od najsuptilnijih shema u cijeloj matematici."

Martin Gardner.

Meta roboti: zagalnite formule brzog množenja, pokažite im zastosuvannya za rješavanje problema.

Menadžer:

1) saznati i sistematizovati informacije iz prve nabavke;

2) riješiti zadatak rješavanja Newtonovog binoma i formule za zbir i razliku koraka.

Objekti koje treba pratiti: Njutnove formule binoma, zbira i razlike.

metode praćenja:

Rad sa primarnom i naučno-popularnom literaturom, internet resursima.

Rozrakhunki, povnyannya, analiza, analogija.

Relevantnost. Ljudi se često dovode majkama s desne strane sa zadataka, u kojima je potrebno dosta pojačati mogući načini roztashuvannya deyakikh objektív chi kílkíst vsíh mozhlivih svodív zdíysnennya deykoí̈ í̈ í̈. Najsvestranijim kombinacijama se dodaju različiti načini chi opcija, koje se donose da biraju ljude. Í tsiliy podijeljena matematika, naslovi kombinatorike, okupirani potragom za različitom ishranom: primjeri svih kombinacija za taj tip chi ínshoy.

Uz kombinatorne vrijednosti, predstavnici raznih specijalnosti dovedeni su do prave majke s desne strane: naučnik-hemičar, biolog, dizajner, dispečer, takođe. Jače interesovanje za kombinatoriku Sat odmora biti pod utjecajem bijesnog razvoja kibernetike i računarske tehnologije.

Entry

Ako želite da potvrdite, da je govornik prevazišao kompleksnost dana, uz neke nedostatke, čini se: Ja sam Newtonov ban! Movlyav, Newtonova osa, sklopiva je, ali ima problema u tebi! O Newtonovom binomu chuli navitt oni ljudi čija interesovanja nisu vezana za matematiku.

Riječ "binom" znači binarni, tobto. zbir dve donacije. W stopa škole slijede nazivi formula kratke množine:

( a+ b) 2 = a 2 + 2ab + b 2 , (a+b) 3 = a 3 +3a 2 b+3ab 2 +b 3 .

Sljedeće formule su formule, kako se naziva Newtonova binomna formula. U školama su pobjedničke formule za širenje na višestruke kvadrate, zbir i različite kocke. Šta je smrad za naredne korake? Dakle, u takvim formulama smrad često pobjeđuje na virišennom zavdanu: da se dokaže lažnost, brzina razlomaka, blizina proračuna.

Razvoj logičkih formula razvija deduktivno-matematičke ideje i duboku retoriku.

DIO 1. NJUTNOVA BINOMSKA FORMULA

Pojdnannya da njihova moć

Neka je X množitelj koji se sastoji od n elemenata. Bilo da je to podmnožitelj Y, multiplikator X, koji zamjenjuje k elemenata, naziva se jedan po jedan k elemenata iz n sa k ≤ n.

Broj različitih stavki k elemenata iz n je dodijeljen n k . Jedna od najvažnijih formula kombinatorike je sljedeća formula za broj n k:

Ono se može zapisati nakon očiglednog ranga koji će uskoro doći:

Zokrema,

Čitava stvar je korisna za tim, da množitelj X ima više od jednog podmnožaka od 0 elemenata - prazan podmnoži.

Brojevi C n k stvaraju niz čudesnih moći.

Formula je važeća n k = n - k n , (3)

Smisao formule (3) zasniva se na činjenici da je konzistentnost jedan-na-jedan između odsustva svih k-terminalnih podmnožnika od X i odsustva svih (n - k)-članih podmnoževa od X: do uspostaviti snagu dovoljnu da skin k-termin submultiple od Y stavi jedan dodatak u množitelj X.

Formula je važeća Z 0 n + Z 1 n + Z 2 n + ... + Z n n = 2 n (4)

Zbir, koji stoji na lijevom dijelu, odražava broj svih podmnožaka od X (C 0 n je broj 0-članih podmnožaka, C 1 n je broj jednočlanih podmnožaka, itd.).

Za bilo koje k, 1≤ k≤ n, jednakost je pravedna

C k n \u003d C n -1 k + C n -1 k -1 (5)

Qiu ljubomoru nije jako važno dobiti za pomoć formule (1). Istinito,

1.2. Visnovok Newtonove binomne formule

Pogledajmo korake binoma a +b .

n = 0, (a +b ) 0 = 1

n = 1, (a +b ) 1 = 1a+1b

n = 2(a +b ) 2 = 1a 2 + 2ab +1 b 2

n = 3(a +b ) 3 = 1 a 3 + 3a 2 b + 3ab 2 +1 b 3

n = 4(a +b ) 4 = 1a 4 + 4a 3 b + 6a 2 b 2 +4ab 3 +1 b 4

n=5(a +b ) 5 = 1a 5 + 5a 4 b + 10a 3 b 2 + 10a 2 b 3 + 5ab 4 + 1 b 5

Poštujemo sljedeće zakone:

Broj članova opsednutog bogatog člana je jedan više za indikaciju stepena binoma;

Indikator koraka prvog dodatka mijenja se od n do 0, indikator koraka drugog dodatka raste od 0 do n;

Koraci svih mononoma jednaki su koracima binoma za um;

Kozhen monom - dodatak prve i druge viraze na različitim nivoima i poslednjeg broja - binomni koeficijent;

Binomni koeficijenti, rívnovíddalení víd kíntsa rozkladannya, ívní.

Da bismo razjasnili ove formule, takva formula se zove Newtonova binomna formula:

(a + b ) n = C 0 n a n b 0 + C 1 n a n -1 b + C 2 n a n -2 b 2 + ... + C n -1 n ab n -1 + C n n a 0 b n . (6)

Za ovu formulu n može biti prirodan broj.

Izvedemo formulu (6). Nasampered, napišimo:

(a + b ) n = (a + b )(a + b ) ... (a + b ), (7)

de broj lukova koji se množe, dorivnyuê n. Od izvanrednog pravila množenja zbroja sa zbirom, nabuja, što viraz (7) bogati zbroj svih velikih tvorevina, kako se može spojiti s ofanzivnim rangom: budi nekakav dodanok prvi od sume a + b pomnožite s bilo kojim dodanokom drugog sumi a+b za neki dodatni novac od treće sume i tako dalje.

Iz rečenog je jasno da je dodankom za (a + b ) n dati (jedan prema jedan) redove dužine n, presavijene od slova i to b. Usred dodankív zustrichatimutsya takvih članova; očito je da se takvim članovima daju redovi, da se osvete isto toliko slova a. Ale, broj redova, koji bi trebao biti jednak k puta slovu a, Dakle sama Z n k . Otzhe, zbir svih članova, za zamjenu slova a množiteljem jednakim k puta, dorívnyuê C n k a n - k b k . Skala k može imati vrijednosti 0, 1, 2, ..., n-1, n, tada je formula (6) vidljiva iz našeg skaliranja. S poštovanjem, (6) može se napisati kraće: (8)

Želeći da formulu (6) nazovemo po Newtonu, zapravo je nazvana čak i prije Newtona (na primjer, poznavajući Pascal). Zasluga Njutna je u tome što zna tačne formule za nekoliko različitih indikacija. Isto ja. Newton na 1664-1665 str. vivív formula, scho vrazhaê stupín binom za dovílny sačmaricu i negativan pokaznív.

Brojevi 0 n , C 1 n , ..., C n n , koji su uključeni u formulu (6), obično se nazivaju binomni koeficijenti, koji se definiraju na sljedeći način:

Iz formule (6) možemo uzeti ceo red snaga ovih koeficijenata. Na primjer, s poštovanjem a=1, b = 1, uzimamo:

2 n = C 0 n + C 1 n + C 2 n + C 3 n + ... + C n n ,

tobto. formula (4). Put Yakshcho a= 1, b = -1, zatim matematika:

0 = Z 0 n - C 1 n + C 2 n - C 3 n + ... + (-1) n C n n

ili C 0 n + C 2 n + C 4 n + ... = C 1 n + C 3 n + + C 5 n + ... .

Tse znači da je zbir koeficijenata uparenih članova rasporeda veći od zbira koeficijenata neuparenih članova rasporeda; njega kože 2 n -1 .

Koeficijenti članova, rívnovíddalení u íd kíncív rozkladannya, ívní. Cijena snage je vyplyvaê íz spívvídnoshennia: Z n k = Z n n - k

Tsíkaviy okremy vipadok

(x + 1) n = C 0 n x n + C 1 n x n-1 + ... + C k n x n - k + ... + C n n x 0

ili kraće (x +1) n = ∑C n k x n - k .

1.3. Polinomska teorema

Teorema.

Dovođenje.

Dakle, nakon otvaranja luka vijšovskog monoma, potrebno je odabrati one lukove, od kojih ćete uzeti, ove lukove, iz kojih uzeti, itd. i tí lukovi, iz kojih su uzeti. Koeficijent za koji se daje monom nakon davanja sličnih pojmova broju načina na koje se takav izbor može napraviti. Prvo heklanje u nizu izbora može se izvesti pomoću sredstava, drugo heklanje - , treće - itd., treće heklanje - od strane advokata. Koeficijent, scho shokaetsya, dorivnyu creat

ROZDIL 2. Pokhídní viših redova.

Razumijevanje Pokhídnih Vishchih sistema.

Neka se funkcija razlikuje u intervalu pjevanja. Todi í̈í̈ pokhídna, vzagalí naizgled, lezi X, to je funkcija X. Otzhe, sto puta iznova, možete razbiti hranu o razlogu za pokhidnoy.

Imenovanje . Pokhídna kao prva pokhídnoí̈ se zove sličan drugom naređenju ili drugom sličnom označen je simbolom inače, tobto

Imenovanje . Pokhídna kao i drugi pokhídnoí̈ naziva se pokhídnoy trećeg reda ili trećeg pokhídnoy i označava se kao simbol.

Imenovanje . Pokhídnyn th order funkcije zove se persha pokhídna u vid pokhídnoí̈ (n -1)-ti red, funkcije i su označene simbolom abo:

Imenovanje . Pokhídní red viši od prvog se nazivaju pronalaženje najgoreg.

Poštovanje. Slično, možete uzeti formulu n-ta sljedeća funkcija:

Još jedna slična parametarski definirana funkcija

Budući da je funkcija parametarski data jednakima, tada vrijednost slične u drugom redoslijedu treba diferencirati na drugačiji način funkcija preklapanja nezavisna promena.

Tako da

to je urahuvannyam to, scho,

Hajde da ga odnesemo.

Slično, možete znati i treći način.

Differential sumi, kreirajte to privatno.

Budući da diferencijal dolazi od sličnih množenja diferencijalu nezavisne varijable, onda se, znajući sličnosti glavnih elementarnih funkcija, kao i pravila za promatranje potonjih, mogu razviti slična pravila za ispitivanje diferencijala.

1 0 . Diferencijalna konstanta na nulu.

2 0 . Diferencijalni zbir algebre konačnog broja derivacija funkcija .

3 0 . Diferencijal na stvaranje dviju funkcija, koje se razlikuju, zbrajajući zbroj kreacija prve funkcije s diferencijalom druge i druge funkcije s diferencijalom prve .

Posljedica. Konstantni množitelj se može okriviti predznakom diferencijala.

2.3. Funkcije, zadaci parametarski, njihovo diferenciranje.

Imenovanje . Funkcija se parametarski zove data, kao rezultat uvredljivih promjena X і kožne funkcije se definiraju kao jednoznačne funkcije u obliku jednog te istog i dodatne promjene - parametrat :

det promjena na granicama.

Poštovanje . Usmjerimo parametarsko poravnanje udjela i elipse.

a) Stupac sa centrom na klupi koordinata i radijusom r napravi parametarsko poravnanje:

b) Zapišimo parametarsko poravnanje za elips:

Isključite opciju t Iz parametarskih linija analitičkih linija moguće je razviti njihove kanonske linije.

Teorema . Koja je funkcija argument tipa y x je parametarski zadano jednakima, de i diferencijacija pomoćut funkcije ta, onda.

2.4. Leibnizova formula

Za znakhodzhennya n-ti red razlike između dvije funkcije, najpraktičnija vrijednost je Leibnizova formula

Hajde uі v- Aktivne funkcije u obliku promjena X, šta može biti gore, bilo nekim redom y = UV. Vislovimo n-ti gubitak kroz izgubljene funkcije uі v .

Možda uzastopno

Lako je uočiti analogiju između viraza za drugi i treći sličan i rasporeda Newtonovog binoma, sličan je drugom i trećem koraku, ali umjesto pokazivanja koraka, trebali bi postojati brojevi koji označavaju redoslijed obrnuto, a same funkcije se mogu smatrati "nultim redom". Vrakhovuychi tse, uzimamo Leibnizovu formulu:

Qiu formula se može upotpuniti metodom matematičke indukcije.

DIO 3. IZJAVA LEIBNIZOVE FORMULE.

Za izračunavanje sličnog izračuna, bilo kojim redoslijedom, ovisno o dvije funkcije, preskačući kasnije, formule za izračunavanje sličnog, ovisno o dvije funkcije, moraju biti Leibnizova formula.

Za dodatne formule možemo pogledati izračunavanje sličnog n-tog reda u dvije funkcije.

primjer 1.

Znati redoslijed druge funkcije

Vídpovídno do termina, prijatelj je dobar - prvi je dobar za prvog, pa

Poznajemo prvi red sličan datoj funkciji pravila diferencijacije i vikorist tabela poslednjeg:

Sada znamo pokhídnu víd pokhídnoí̈ prvog reda. Tse će biti šukana drugačijim redoslijedom:

prijedlog:

guza 2.

Znati sljedeći redoslijed funkcija

Rješenje.

Znat ćemo sekvencijalno sljedeću, drugu, treću i tako redove veličine date funkcije kako bismo uspostavili pravilnost, tako da možete reći sljedeću.

Idemo prvi red, znamo kako idi privatno:

Ovdje se viraz naziva faktorijel broja. faktorijel

Pokhídna drugog reda, prva, prva, prva, ona

Pokhídna trećeg reda:

Četvrti je dobar:

Poštujemo pravilnost: brojilac ima faktorijel broja, koji je više kao redosled lošijeg, a u znameniku je korak korak više, što niži red to je bolji, tako da

Vidpovid.

primjer 3.

Znati vrijednost treće slične funkcije u jednoj tački.

Rješenje.

Zgidno tablice sličnih viših reda, možda:

Čija guza, tobto otrimuemo

S poštovanjem, da bi se takav rezultat mogao oduzeti za sukcesivnu vrijednost potonjeg.

Kod zadatka, treća tačka je skuplja:

prijedlog:

guza 4.

Upoznajte omiljene karakteristike prijatelja

Rješenje. Za klip znamo pershu pokhídnu:

U svrhu poznavanja još jednog sličnog slučaja, još jednom razlikuje virazu za prvi sličan slučaj:

prijedlog:

Primjer 5.

Znaj, yakscho

Ako je funkcija data kao dopuna dvije funkcije, tada će analogna vrijednost četvrtog reda dodati Leibnizovoj formuli:

Znamo sve dobre stvari i bojimo se koeficijenata sa dodacima.

1) Porahuêmo coefítsíênti sa dodanki:

2) Znamo slične funkcije:

3) Znamo slične funkcije:

prijedlog:

Primjer 6.

Zadata funkcija y=x 2 cos3x. Znajte trik trećeg reda.

Neka je u = cos3x, v = x 2 . Isto i za Leibnitzovu formulu koju poznajemo:

Pokhídní koga možete pogledati:

(cos3x)′=−3sin3x,

(cos3x)′′=(−3sin3x)′=−9cos3x,

(cos3x)′′′=(−9cos3x)′=27sin3x,

(x2)′=2x,

(x2)′′=2,

(x2)′′′=0.

Otzhe, treća pokhídna data funkcija je skuplja

1 ⋅ 27sin3x ⋅ x2+3 ⋅ (−9cos3x) ⋅ 2x+3 ⋅ (−3sin3x) ⋅ 2+1 ⋅ cos3x ⋅ 0

27x2sin3x−54xcos3x−18sin3x=(27x2−18)sin3x−54xcos3x.

Primjer 7.

Know pokhidnu n funkcije -th reda y=x 2 cosx.

Ubrzavanje sa Leibnitz formulom, s obziromu=cosx, v=x 2 . Todi

Ostali članovi serije jednaki nuli, krhotine(x2)(i)=0 za i>2.

Pokhidna n kosinus funkcija -tog reda:

Otzhe, pokhídna naše funkcije su dobre

WISNOVOK

U školi se uvijaju i pobjeđuju sljedeće formule brzog množenja: kvadrati i zbirovi i zbroji dva zbroja, te zbroji i zbroji dva zbira zbira i zbirovi dva zbira. Sljedeće formule su formula, nazvana Newtonova binomna formula, i formula za proširenje u višestruke sume i razlike koraka. Brojne formule često pobjeđuju na virishenní ríznih zavdanu: dokazati lažnost, brze razlomke, blizinu izračunavanja. Posmatra se moć Pascalovog trick-or-treater-a, usko vezana za Newtonov binom.

Robot je sistematizirao informacije o temi, primijenio zadatak postavljanja Newtonovog binoma i formule zbira i razlike koraka. Robot se može koristiti u robotskoj matematičkoj grupi, kao i za samostalnu grupu Timisa, koji se bavi matematikom.

SPISAK DŽERELOVIH POBJEDA

1. Vilenkin N. Ya. Kombinatorika.- pogled. "Nauka". - M., 1969.

2. Mikilsky S.M., Potapov M.K., Reshetnikov N.M., Shevkin A.V. Algebra i klip matematičke analize. Ocjena 10: Navch. za zagalnosvít. organizacija temeljnih i ukopa reka - M.: Prosvitnitstvo, 2014. - 431 str.

3. Rješenje problema statistike, kombinatorike i teorije imovirnosti. 7-9 ćelija. / Autor - styling V.M. Studenetska. - Pogled. 2., Vipr. - Volgograd: Vchitel, 2009

4. Savushkina I.A., Khugaev K.D., Tishkin S.B. Algebarsko poravnanje višim stepenicima /metodička pomoć za slušanje studenata odsjeka za međuuniverzitetsku obuku - Sankt Peterburg, 2001.

5. Sharigin I.F. Izborni predmet iz matematike: Rješavanje problema. Glavna pomoć za 10 ćelija. srednja skola. - M: Prosvitnitstvo, 1989.

6.Nauka i život, Newtonov binom i Pascalov triko[Elektronski izvor]. - Način pristupa: http://www.nkj.ru/archive/articles/13598/

Pokhídní viših redova

U ovom uzrastu učimo da poznajemo niže redove, a takođe i zapisujemo uobičajenu formulu nižeg reda. Osim toga, Leibnizova formula će se posmatrati kao takva slična i brojčana prohanja - slična višim redovima veličine implicitno definirane funkcije. U iskušenju sam da uradim mini-test:

Funkcija osi: i axis í̈í̈ persha pokhídna:

U tom raspoloženju, pošto ste okrivili neke poteškoće/nerazumljive stvari, budite ljubazni, pročitajte dva osnovna članka mog kursa: Kako da znam da li ću ići?і Funkcija preklapanja. Nakon savladavanja elementarnih pokhídnyh, preporučujem vam da naučite iz lekcije Najjednostavniji zadatak za sahranu, na kojem smo se digli, zokrema z drugi pokhídny.

Nije važno pogoditi da je prijatelj loš - loš je kao i prvi loš:

U principu, ostaviću prijatelja, ali vzhe vvazhayut na sličan način.

Slično: treće je gore - isto je gore nego drugo je gore:

Četvrta pokhídna - ê pokhídna víd 3-í̈ pokhídnoí̈:

P'yata je dobra: , i očito je da sve sličnosti viših redova mogu biti jednake nuli:

Krimska rimska numeracija u praksi često ima sljedeće oznake:
, Označimo "energetski" poredak kroz. Uz to, indeks superstrune treba položiti na okov.- da vaskrsne smrt "gravitacije" svijeta.

Ponekad postoji takav zapis: - Treće, četvrto, p'yata, ..., "Enna" je slično.

Naprijed bez straha i sumnívív:

guza 1

Zadata funkcija. Znaj.

Rješenje: Šta se tu može... - samo napred za četvrto dobro :)

Chotiri stavlja poteze već nisu prihvaćene, pa idemo na numeričke indekse:

Vidpovid:

Dobro, ali sada razmislimo o takvoj hrani: zašto raditi, ako je potrebno da um zna ne 4., već, na primjer, 20. Umrijet ću? Yakshcho za marš 3-4-5 (maksimalno, 6-7.) Redoslijed odluke je donesen da se to završi brzo, tada nećemo "doći" do sljedećeg višeg reda, oh, jao, ne uskoro. Ne zapisujte istinu 20 redova! U sličnoj situaciji potrebno je analizirati uzorak poznatih, utvrditi pravilnost i formulisati formulu slične. Dakle, u Primjeni br. 1, lako je shvatiti da se u slučaju kožne ofanzivne diferencijacije ispred eksponenta „viskozitet“ dodaje dodatna „tri“, štaviše, na najkraćem koraku od „trojke“, to je više kao broj gorih, takođe:

De je prilično prirodan broj.

Yakshcho, onda izađi tačno 1. loše: yakscho - zatim 2-a: i itd. U takvom rangu, dvadeset pokhídna vyznaêtsya mittevo: - I sljedeći "kilometarski dio"!

Igranje samostalno:

guza 2

Znati funkcije. Zapišite sistem

Rješenje je slijediti primjer lekcije.

Nakon zagrijavanja, šta poboljšati, možemo pogledati više sklopivih guza, na neke praktične načine, algoritam rješenja. Tim, koji je naučio lekciju Između sekvenci, budi troch lakse:

guza 3

Znati funkcije.

Rješenje: da razjasnimo situaciju, znamo nekoliko od sljedećeg:

Množenje brojeva nije brzo! ;-)


Mabut, godina. ... Navit trohi pretjerao.

Na ofanzivu krotsí, najbolje je dodati formulu “ení̈” pokhídnoí̈. (ako ti ne smeta pamet, onda se možeš slagati sa crncem). Za koga se čudimo odbijanju rezultata, vidimo regularnost kojom je koža napadnuta.

Prije svega, smrad zna đavoli. Znak za red je siguran "bliskalica", a dijelovi 1. su pozitivni, onda ću upotrijebiti formulu da vidim uvredljivi množitelj: . Pídíyde th ekvivalentna varijanta, ali posebno ja, kao optimista, volim znak plus \u003d)

Na drugačiji način, brojilac "navija" faktorijel, štoviše, VIN "vídstaê" víd pokhídní brojevi po jednoj jedinici:

Í na treći način, koraci „dvojke“ rastu na numeralistu, kao da je broj sličan. Isto se može reći i za korake bannermana. Ostatak:

Iz metode ponovne provjere možemo zamijeniti nekoliko vrijednosti "en", na primjer, i:

Za čudo, sada će početi pomilovanja - samo grijeh:

Vidpovid:

Jednostavna funkcija za nezavisna odluka:

guza 4

Znati funkcije.

Í zavdannya tsikavíshe:

guza 5

Znati funkcije.

Ponovimo red još jednom:

1) Znamo nekoliko papalina mrtvih. Da biste uhvatili zakone, zazvonite na triokh-chotiriokh.

2) Onda toplo preporučujem preklapanje (Želio bih koristiti crnu)"Ennu" će nestati - garantovano će biti na obali pred pomilovanjem. Ale se može poništiti i bez, tobto. razmisli o tome i zapiši, na primjer, umrijet ću u dvadeset osmoj. Više od toga, deakí ljudi vzagalí zdatní víríshiti tsí zavdannya usno. Međutim, sljedeća stvar koju treba zapamtiti je da "Shvidki" može zaprijetiti, radije biti siguran.

3) U završnoj fazi, potrebno je ponovo provjeriti "en" pokhidnoy - uzimamo nekoliko vrijednosti "en" (kraće za sudove) i potkrepimo zamjenu. A još bolje je preispitati sve što se ranije znalo. Ako je nešto predstavljeno u potrebi za značenjem, na primjer, i rezultat je precizno izračunat.

Kratko rješenje 4 i 5 primjera za lekciju.

U nekim zadacima, da bi se riješili problemi, potrebno je malo popraviti funkciju:

guza 6

Rješenje: Ne želim da razlikujem predloženu funkciju, ne želim, krhotine "prljavog" driblinga, koje uvelike otežavaju odbijanje nadolazećih pokhídnyh.

Za koga dotsilno vikonati ispred transformacije: vikoristovuemo formula kvadratne razlikeі snaga logaritma :

Zovsím ínsha na desnoj strani:

ja stari prijatelji:

Mislim da se sve vidi. Odajte poštovanje, još jedan loš znak je nacrtan, a prvi - ne. Konstruišemo sličan sistem:

kontrola:

Pa, za ljepotu, faktor za ruke:

Vidpovid:

Tsíkave zavdannya za nezavisnu vyríshennya:

guza 7

Napišite formulu istim redoslijedom za funkciju

A sada o neprikosnovenoj međusobnoj odgovornosti, a to je da čestitam italijanskoj mafiji:

guza 8

Zadata funkcija. Znaj

Vísímnadtsyata pokhídna u točki. Usyogo.

Rješenje: leđa uz leđa, očigledno, potrebno je znati Idemo:

Popravili su sinus, došli do sinusa. Bilo je jasno da je za dalju diferencijaciju ovaj ciklus trivijalan, i da okrivljuje istu moć: kako se brže „udaljiti“ do osamnaestog veka?

„Amaterska“ metoda: na šalteru je lako zapisati desnom rukom broj nadolazećih mrtvih:

na ovaj način:

Ale tse pratsyuê, kao da red pokhídnoi nije tako sjajan. Pa, moram da znam, recimo, izaći ću iz ćelije, ubrzaću podilnistyu za 4. Stotinu podijeliti na čotire bez viška, a lako je baciti, jer se takvi brojevi valjaju u donjem redu, do toga:.

Prije govora, 18 pokhídnu tezh može se razlikovati od sličnih mirkuvana:
drugi red ima brojeve, koji su podijeljeni sa 4 od viška 2.

Drugi, više akademski način osnivanja periodičnost do sinusaі formule za vođenje. Koristuyemosya gotova formula "enoi" slična sinusu , u jaku je potreban broj jednostavno prikazan. Na primjer:
(formula za smanjenje ) ;
(formula za smanjenje )

Za naše stanovište:

(1) Pošto je sinus periodična funkcija sa tačkom, onda se argument može bezbolno „okrenuti“ na 4. period (tobto.).

Pokhídnu sistem víd vykonannya dvoh funktsíy može biti poznat po formuli:

Zokrema:

Ne morate ništa posebno pamtiti, jer što više znate formule, manje ih razumijete. Saznajte više o priči Njutnov binom oskílki Leibnizova formula je sve sličnija novoj. Pa ti imaš sreće, kako pobjeći od 7. ili višeg reda (koji je, međutim, mali), bit ćete posramljeni. Vtím, ako cherga didde to kombinatorika- to je svejedno ponijeti =)

Znamo treću sličnu funkciju. Koristimo Leibnitzovu formulu:

U ovom pogledu: . Pokhídní se lako prevodi usmeno:

Sada pažljivo i s poštovanjem zamjena i jednostavan rezultat:

Vidpovid:

Sličan zadatak za nezavisnu viziju:

guza 11

Znati funkcije

Ako bi se u prednjem dijelu stražnjice rješenje "na čelu" i dalje natjecalo s Leibnizovom formulom, onda bi to bilo s pravom neprihvatljivo. I još neprihvatljivije - drugim redoslijedom, to je još gore:

guza 12

Znajte tačan redoslijed

Rješenje: prvo i osnovno poštovanje - okrećite osovinu ovako, pojedinačno, nije potrebno =) =)

Zapišimo funkcije i znamo njihove sličnosti do 5. reda uključujući. Priznajem da su ti koraci sa desne strane postali pospani:

S lijeve strane "uživo" loše stvari su "završile" i još je bolje - u Leibnizovoj formuli, tri dodavanja su resetirana na nulu:

Muči me dilema, shvatio sam je u članku o folding pokhídnyh: chi pitati rezultat? U principu, možete ga izostaviti i tako - lakše ga je obrnuti. Ale vin može pomoći u donošenju odluke na pravi put. S druge strane, oproštena na snazi ​​inicijative, prijetim algebri pomilovanjem. Međutim, imamo ê vídpovíd, otrimana "primarni" način =) (Div. poslao u klip), i slažem se, vin je tačan:

Dobro, sve je u redu.

Vidpovid:

Sretan zadatak za samostalnu viziju:

guza 13

Za funkciju:
a) označavaju direktnu diferencijaciju;
b) znati iza Leibnizove formule;
c) izračunati.

Ne, nisam sadista - tačka "a" ovde je oproštena =)

I još ozbiljnije, onda „direktno“ rješenje posljednjih diferencijacija može imati i „pravo na život“ - na više načina, savijanje može biti jednako savijanju Leibnizove formule. Vykoristovyte, kao da poštujete dotsílne - malo je vjerovatno da ćete biti osnova malog zadatka.

Ukratko, rješenje je da se ilustruje lekcija.

Da bismo podigli završni paragraf, potrebno je zapamtiti razlikovati implicitne funkcije:

Promjene u višim redovima funkcija, poslovi implicitno

Bogat neko od nas vitrativ dovgí godina, dana i tizhní život na vvchennya kíl, parabola, hiperbola- a ponekad se i kažnjavalo. Pa hajde da se osvetimo i razdvojimo ih kao trag!

Pochnemo zí "shkílnoí̈" parabola za nju kanonski logor:

guza 14

Rivnyanya je data. Znaj.

Rješenje: prvi krok dobro znanje:

One koje funkcionišu da í̈í̈ pokhídna vírazhení implicitno ne mijenjaju suštinu, druga je pokhídna - tse pokhídna víd 1. í̈ pokhídnoí̈:

Međutim, potrebno je uspostaviti vlastita pravila: samo preko "iks" i "iplayer". Na to u otrimanu 2. pokhídnu zamislimo:

Treća pokhídna - ê pokhídna víd 2-í̈ pokhídnoí̈:

Slično, zamislite:

Vidpovid:

"Škilna" hiperbola u kanonski logor- za samostalan rad:

guza 15

Rivnyanya je data. Znaj.

Ponavljam, izgubiću 2. i rezultat treba objasniti samo kroz "iks" / "iplayer"!

Ukratko, rješenje je da se ilustruje lekcija.

Nakon djetinjastih namotaja, diveći se njemačkoj pornografiji @fiyu, izgledamo zrelije guzice iz kojih znamo još jednu bitnu odluku:

guza 16

Elips dominantna osoba.

Rješenje: znamo 1. pokhídnu:

A sada se prisjetimo i analizirajmo nadolazeći trenutak: možemo odmah razlikovati, tako da ne moramo šutjeti. U ovakvom stanju duha, krajnje je jednostavno, ali u stvarnosti, naredbe takvih darova daju se dvaput i jednom na vlasti. Koji je najbolji način da se riješite glomaznog pokhidnoja? Ísnuê! Izjednačavamo i pobjeđujemo istim trikom da, kada se zna 1., objesimo udarce na vrijeđajuće dijelove:

Druga pokhídna je kriva, ali se izražava samo kroz ovo i ono u isto vrijeme (odjednom) pokhidnoy. Za koga je u Otrimanu zamislivo jednako:

Da biste se riješili većine tehničkih poteškoća, pomnožite štetne dijelove sa:

I manje u završnoj fazi, sastavljamo dríb:

Sada se čudimo vihídne rívnyannya, i napominjemo da ako se rezultat oduzme, to bi trebalo biti oprošteno:

Vidpovid:

Kako znati značenje 2. pokhídnoí̈ u bilo kojoj tački (yaka, zrozumílo, lezi na elípsu), na primjer, u tački ? Prelagano! Tsej motiv već zustríchavsya na lekciji o jednake normale: u virase 2, potrebno je predstavljati :

Ludo, na sva tri načina možete oduzeti eksplicitno date funkcije i razlikovati ih, ali i moralno prilagoditi praksu sa dvije funkcije, kao da se osvetite korijenu. Po mom mišljenju, bilo bi bolje donijeti odluku „implicitnim putem“.

Konačni primjer za nezavisnu viziju:

guza 17

Pronađite implicitno definiranu funkciju

Leibnizova formula za broj n-tog sličan rad dvije funkcije. Nadano je dokaz na dva načina. Pogledao sam zadnjicu obračuna n-tog reda.

Zmist

Div. također: Pokhídna robot dvije funkcije

Leibnizova formula

Uz pomoć Leibnizove formule, možete izračunati gubitak n-tog reda u dvije funkcije. Vaughn može izgledati ovako:
(1) ,
de
- Binomni koeficijenti.

Binomni koeficijenti sa koeficijentima distribucije binoma za korake i:
.
Dakle, broj je broj istog dana s n k .

Dokaz Leibnizove formule

Nađimo formulu za poboljšanje dvije funkcije:
(2) .
Formulu (2) prepisujemo na sljedeći način:
.
Stoga smo svjesni da se jedna funkcija deponuje u obliku promjene x, a druga - u obliku promjene y. Na primjer, poštujemo rozrahunka. Prethodna formula se može napisati na sljedeći način:
(3) .
Oscalls su slični zbiru pojmova, a skin termin je zbrajanje dvije funkcije, tada za izračunavanje nižih redova možete sukcesivno postaviti pravilo (3).

Isto za sličan n-ti red možda:

.
Vrahovyuchi, scho i mi otrimuemo Leibnizova formula:
(1) .

Dokaz indukcijom

Dokažimo Leibnizovu formulu matematičkom indukcijom.

Još jednom pišemo Leibnicovu formulu:
(4) .
Za n = 1 moguće je:
.
Ova formula je slična praksi dvije funkcije. Vaughn je u pravu.

Pretpostavimo da formula (4) vrijedi za sličan n-ti red. Može se pokazati da vrijedi za sličan n+ 1 th order.

Diferencijal (4):
;



.
Oče, znali smo:
(5) .

Stavimo to u (5) i možemo reći da:

.
Može se vidjeti da formula (4) može izgledati isto za sličan n + 1 th order.

Kasnije, formula (4) vrijedi za n = 1 . Brinite se, što je osvojeno za decimalni broj n = m 1 .
Leibnizova formula je završena.

guza

Nabrojite n-tu slučajnu funkciju
.

Hajde da riješimo Leibnizovu formulu
(2) .
Po našem ukusu
;
.

Iza stola nedavnih majki:
.
Zastosovuêmo moć trigonometrijskih funkcija:
.
Todi
.
Može se vidjeti da je diferencijacija sinusa funkcije dovedena do zsuv na . Todi
.

Znamo slične funkcije.
;
;
;
, .

Oskílki na , tada Leibnizova formula ima više od tri prva člana u obliku nule. Znamo bínomní koefítsíênti.
;
.

Iza Leibnizove formule može stajati:

.

Div. također: