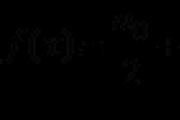Taisyklės yra tai, kad diferenciacijos formulės gaunamos iš lankstymo funkcijų. Tinka sulankstymo funkcijai

Funkcijos sulankstomas laikrodis terminas „sulankstymo funkcija“ nėra dar teisingesnis. Pavyzdžiui, viglyada dar labiau perkonvertuota, bet lankstymo funkcija ne є, į vidminu iš.

Ar tsіy statty mi atsipalaiduok su supratimu sulankstymo funkcija, kurį galima pamatyti elementariųjų funkcijų sandėlyje, yra formulė, leidžianti pažinti paprasčiausią ir praneštiną būdingų priedų sprendimą.

Kai pirmą kartą taikysite jį visam laikui, pamatysite senų ir diferencijavimo taisyklių lentelę, todėl apkarpykite jas prieš akis.

Sulankstymo funkcija- Visa funkcija, argumentas taip pat yra funkcija.

Mūsų nuomone, kaina yra geriausia vertė. Visiškai įmanoma reikšti f (g (x)). Tobto, g (x) yra funkcijos f (g (x)) argumentas.

Pavyzdžiui, jei f yra arctangento funkcija, o g (x) = lnx yra natūraliojo logaritmo funkcija, tada lankstymo funkcija f (g (x)) є arctan (lnx). Taip pat užpakalis: f - reguliavimo funkcija ketvirčio žingsniais ir - tsіla racionali funkcija (stebuklas), todі .

Jūsų tempu g (x) gali būti sulankstymo funkcija. Pavyzdžiui, ... Galima pagalvoti apie tokį virazą jaką ... Čia f yra sinuso funkcija, yra kvadratinės šaknies funkcija, - Shot racionali funkcija. Logiška tai paleisti, kad būtų galima atlikti funkcijų indėlio žingsnius natūralusis skaičius.

Dažnai galima iškviesti lankstymo funkciją kompozicijos funkcijos.

Znakhozhennya pohid lankstymo funkcijos formulė.

užpakalis.

Žinokite lankstymo funkciją.

Sprendimas.

Apskritai f yra kvadratinė funkcija, o g (x) = 2x + 1 yra tiesinė funkcija.

Ataskaitos ašis pagrįsta funky lankstymo funkcijos formulėmis:

Žinok, kad išeisiu, priešais atleidęs vizualinę funkciją.

Otzhe,

Jakas bachitas, rezultatai yra sb_gayutsya.

Neapgaudinėk, kaip funkcija є f, bet kaip g (x).

Aišku, už pagarbos užpakalis.

užpakalis.

Žinokite originalias sulankstymo funkcijas, kurios.

Sprendimas.

Pirmajam f yra kvadratinė funkcija, o g (x) yra sinuso funkcija, taigi
.

Kitame f yra sinuso funkcija ir būsenos funkcija. Otzhe, formulei dobutku lankstymo funkcija maєmo

Funky funkcijos formulė

užpakalis.

Funkcionalumas .

Sprendimas.

Naudodami daugybę lankstymo funkcijų, galite sumaniai įrašyti jaką , de – sinuso funkcija, trečiosios pakopos įvedimo funkcija, logaritmo funkcija ekrane, arktangento paėmimo funkcija ir linijinė rodymo funkcija.

Funky sulankstymo funkcijos formulei

Dabar mes žinome

Kartu parenkame pramoninius rezultatus:

Baisus nichogo kvailas, sutvarkyk lankstymo funkcijas kaip matrioshka.

Apskritai, galite baigti straipsnį, yakby zhodne ale ...

Bazhano aiškus samprotavimas, jei nustatote diferenciacijos taisykles ir senųjų lentelę, ir jei senų lankstymo funkcijų formulė.

BŪKITE YPAČ ATSARGIAI. Mes kalbėsime apie sulankstymo funkcijų funkcionalumą. Dėl to, kad turėsite gerą idėją apie tai, ir jums seksis su senaisiais.

Beveik iš paprastų akcijų. funkcija galite pažvelgti į jako raukšlę: g (x) = tgx, ... Otzhe, galite iš karto naudoti funky lankstymo funkcijos formulę

Ir funkcijos ašis jo negalima pavadinti sulankstomu.

Qia funkcija є trijų funkcijų suma, 3tgx і 1. Noriu - є lankstymo funkcija: - būsenos funkcija (kvadratinė parabolė), o f - liestinės funkcija. Tam yra sumi diferencijavimo formulės rinkinys:

Jau per vėlu žinoti lankstymo funkciją:

Tomas.

Spodіvaєmosya, jūs užfiksavote esmę.

Jis gali būti stebėtinai platesnis, gali būti naudojamas, sulankstymo tipo funkcija gali būti įtraukta į lankstymo funkcijų sandėlį, o sulankstymo funkcijos gali būti naudojamos kaip sulankstymo funkcijos saugojimo dalys.

Jako užpakalis, kurį reikia paimti, kad būtų galima saugoti dalis .

Perche tai yra lankstymo funkcija, kaip ji gali būti pavaizduota peržiūros priemonėje, de f yra logaritmo funkcija ekrane 3, o g (x) yra dviejų funkcijų suma і ... Tobto, .

Kitu būdu Naudokime funkciją h (x). Laimėjo vidnoshennyam į .

Tse dviejų funkcijų suma , de - Sulankstoma funkcija su skaitmeniniu našumu 3. - kubo funkcija; - kosinuso funkcija; - linijos funkcija.

Tse suma dvi funkcijos i, de - sulankstymo funkcija, - eksponentinė funkcija, - naujausia funkcija.

Esant tokiam rangui,.

By-tertє, eikite į, yaka є tvir lankstymo funkcija ta visa racionali funkcija

Kvadratavimo funkcija yra logaritmo funkcija ekrane e.

Otzhe,.

Pidsumuєmo:

p align = "justify"> Dabar tapo matoma intelekto funkcijos struktūra, tokia kaip formulės ir paskutine apibrėžimo prasme diferenciacijos metu.

Paskirstant diferencijavimo funkcijas (senos žinios) Galite pasimokyti iš kitų įmonių sąrašo.

Priešakiniam artilerijos pasiruošimui bus mažiau baisių užpakalių su 3-4-5 įterptomis funkcijomis. Galite, jei užlipsite ant dviejų užpakalių, būsite pastatyti kaip sulankstoma figūra, jei esate visceralesnis (ar kenčiate), visa kita diferencialiniame skaičiavime taps vaikiška.

2 užpakalis

Žinokite prarastą funkciją

Jakas reiškė, kad naudojant pažįstamą elementarią sulankstymo funkciją, būtina teisingai ROSIBRATISYA prie užstato. Ramiuose vipaduose, jei spėju, spėju cinamono prijomą: paimame, pavyzdžiui, reikšmę "x" ir pabandome (či mintys juodai) įvesti reikšmę į "baisų virazą".

1) Turime suskaičiuoti viraz skaičių, suma yra geriausia investicija.

2) Tada reikia apskaičiuoti logaritmą:

4) Pakeiskite kosinusą į kubą:

5) Pakilimo apačioje:

6) І, nareshty, svarbiausia funkcija yra kvadratinė šaknis:

Lankstymo funkcijos diferenciacijos formulė zastosovayutsya rotacine tvarka, nuo savaime vadinamos funkcijos iki vidinės. Virishuumo:

Nachebto be atleidimo:

1) Aš paimu iš kvadratinės šaknies.

2) Paimsiu iš kainos, vikaristų taisyklės

3) Yra trys maršrutai iki nulio. Iš kito dodanku nuimu nuo laiptelio (kubo).

4) Imu iš kosinuso.

6) Aš, nareshty, paimsiu iš svarbiausios investicijos.

Galite eiti dar svarbiau, bet vis tiek ne geriausio gyvūno užpakaliukas. Pažiūrėkite, pavyzdžiui, Kuznotsovo kolekciją ir įvertinkite visą rožinio, vaikiško grožį ir paprastumą. Kai pagalvoju, man patiks eiti miegoti, persvarstyti, kuris protas yra studentas, kaip žinau, ir atsisakysiu lankstymo funkcijos, kuri nėra dėmesinga.

Įžeidžiantis savarankiško sprendimo užpakalis.

3 užpakalis

Žinokite prarastą funkciją

Pidkazka: bendrų tiesiškumo taisyklių rinkinys ir kūrybos diferenciacijos taisyklė

Už sprendimo ribų tai tarsi pamoka.

Atėjus valandai eiti į chogos kompaktiškesnius ir mielesnius.
Nejuokinga situacija, nes užpakalyje yra ne dvi, o trys funkcijos. Kaip žinoti, kad pasirinksiu tris daugiklius?

4 užpakalis

Žinokite prarastą funkciją

Esu nustebęs, bet kodėl neįmanoma paversti trijų funkcijų į dvi? Pavyzdžiui, jei mūsų darbe yra du galandimai, tada galima sukurti kritinę lanką. Ale taikant visas kūrimo funkcijas: žingsnius, eksponentą ir logaritmą.

Tokiais atvejais būtina pagaliau zasosuvati skirtumo kūrėjui taisyklė du kartus

Dėmesys sutelkiamas į tai, kad s „y“ reiškia dvi funkcijas:, o „ve“ th yra logaritmas:. Kodėl tu gali tai padaryti? A hiba - tse ne tvir du daugikliai ir taisyklė nepraktiška? Nichogo sulankstomas nutildymas:

Dabar tai užgožia taisyklė į lanką:

Vis tiek galite pykti ir kaltinti dėl lankų, arba, šiuo atveju, gražiau atrodyti tokiu požiūriu – lengviau pakeisti.

Į užpakalį galima pažiūrėti ir kitaip:

Verishennya būdo įžeidimas yra visiškai teisingas.

5 užpakalis

Žinokite prarastą funkciją

Savarankiško tirpalo užpakalis, tuo pačiu ir pirmasis būdas.

Aišku analogiški užpakaliukai su trupmenomis.

6 užpakalis

Žinokite prarastą funkciją

Čia galite eiti kilkomos takais:

Už tai:

Visas sprendimas kompaktiškiau užrašyti, kaip visų pirma, privataus diferenciacijos taisyklę , Priimama visai datai:

Iš principo buvo parodytas užpakalis, o jei pametėte jį tokiame vaizde, tai nebus pasigailėjimo. Be valandos akivaizdumo, jį lengva išversti į černetus, bet kodėl to negalima atleisti?

Nukreipkite skaičių į spіlnomniki ir pridėkite trijų viršutinių dalių trupmeną:

Minus dodatkovyh atleisk lauką už tai, kad є rizikinga gauti atleidimą jau ne pažįstamuose senuose, o banaliose mokyklos reinkarnacijose. Kita vertus, vaikui nelengva barti darbuotoją ir prašyti, kad jis „atvestų iki galo“ pasiklydusį.

Paprastas užpakalis nepriklausomam peržiūrai:

7 užpakalis

Žinokite prarastą funkciją

Prodovzhumo įvaldo prijomiją ir nešvankybių išmanymą ir iš karto pastebimi tipiški vipadokai, jei diferencijavimui siūlomas „siaubingas“ logaritmas.

Skirtumo darymo operacija vadinama diferenciacija.

Sprendžiant uždavinius apie senųjų išvedimą iš paprasčiausių (ir net ne paprastesnių) funkcijų, panašių priskyrimo tarp didinimo atlikimo į argumento tobulinimą, buvo pateikta senųjų apibrėžimų lentelė. taisyklių. Pirmieji senuosius šventė Izaokas Niutonas (1643-1727) ir Gotfridas Vilgelmas Leibnitsas (1646-1716).

Tam mūsų valandą noriu žinoti, ar būsiu funkcija, man nereikia sugalvoti, kaip atspėti skirtumą tarp skirtingų funkcijų, kad patobulinčiau argumentą, bet būtina atimti iš lentelės kuo greičiau tos pačios diferenciacijos taisyklės. Norėdami sužinoti skurdžiausiųjų, eikite į įžeidžiantį algoritmą.

Aš žinosiu, kad eisiu, reikalauja viraz po brūkšnelio ženklu grįžti į sandėlius su paprastomis funkcijomis tokia prasmė, kaip diyami (tvir, suma, privatus) megztas ir funkcija. Senųjų elementariųjų funkcijų atstumas žinomas iš senųjų lentelių, o senųjų formulės, tų dalių suma - iš diferenciacijos taisyklių. Lentelė sena ir taisyklės, kaip atskirti duomenis nuo pirmųjų dviejų užpakalių.

atsarga 1.Žinokite prarastą funkciją

Sprendimas. 3 diferenciacijos taisyklės z'yasovuєmo, kuri prarandama funkcijų suma є senųjų funkcijų suma, tobto.

Iš senųjų lentelių „xa“ yra senoji, o senasis sinusas – kosinusas. Pinigų pirkimui iš pagyvenusių žmonių krepšio ir, žinoma, man reikės juos gauti:

atsarga 2.Žinokite prarastą funkciją

Sprendimas. Atskyrimas važiuosiu į Sumi, į kažkokį kitą dodanoką su nuolatiniu daugikliu, kurį galiu kaltinti dėl blogo ženklo:

Vos suradus maistą, paimamos žvaigždės, smarvės, kaip taisyklė, aiškėja perskaičius senesnių lentelę ir paprasčiausias atskyrimo taisykles. Prieš juos mi i praeinu vienu metu.

Pasenusių paprastų funkcijų lentelė

1. Atrodo kaip konstanta (skaičius). Ar tai būtų skaičius (1, 2, 5, 200 ...), kaip є virazi funkcijoje. Nustatykite duris į nulį. Dar svarbiau atsiminti, kad tai būtina dar dažniau
2. Pochіdna aikštė žieminė. Dauguma "Iksa". Nustatykite durų bloką. Labai svarbu įsiminti nadovgo
3. Pochidnos pakopa. Pirmos valandos žingsniais būtinas pastato atgaivinimas, kad būtų atkurta ne kvadratinė šaknis.
4. -1 žingsnyje atrodo kaip žiemiška
5. Kaip kvadratinė šaknis
6. Sinuso takas
7. Galimas kosinusas
8. Ant liestinės
9. Panašus į kotangentą
10. Panašus į arcsiną
11. Panašus į arkosiną
12. Jis panašus į arktangentą
13. Atrodo kaip lanko kotangentas
14. Panašus į natūralųjį logaritmą
15. Logaritminės funkcijos perjungimas
16. Rodiklis rodomas
17. Pasivaikščiojimo šou funkcija

Diferencijavimo taisyklės

1. Pochіdna sumi chi rіznitsі
2. Eikite kurti
2a. Eina virazi padaugintas iš pastovaus daugiklio
3. Atrodo kaip eilinis
4. Ideali lankstymo funkcija

1 taisyklė.Funkcijos

diferenciacija kai kuriuose taškuose, tada tuose pačiuose diferenciacijos ir funkcijų taškuose

kuriuo

tobto. Prarandama ankstesnės senųjų funkcijų algebrų sumos algebrinių funkcijų suma.

Slidstvo. Kadangi yra dvi funkcijos, kurios skiriasi, prisitaiko prie seno priedo, tada senosios, tobto.

2 taisyklėFunkcijos

diferencijuota deyakiy taškais, po to tame pačiame taške diferencijuota ir

kuriuo

tobto. Robotas yra pagrobtas iš dviejų funkcijų, kad būtų sukurtos odos funkcijos roboto pagrobimui.

Aistra 1. Dėl blogo ženklo galima kaltinti nuolatinį daugiklį:

Aistra 2. Galite sukurti dekoratyvines funkcijas, kaip atskirti, visoms galite sukurti daugybę seno odos specialisto kūrinių.

Pavyzdžiui, trims daugintuvams:

3 taisyklėFunkcijos

diferencijuojami deyakiy taškais і , tada tame pačiame taške jis yra diferencijuojamas ir yra privatusu / v, be to

tobto. Privačios dvi funkcijos prarandamos kelio daliai, є skaičius yra.

De scho shukati kitose pusėse

Esant pažįstamiems, nepadoriems kūriniams ir tikrojo personalo dalims, statute būtina iš karto nustatyti keletą diferenciacijos taisyklių, tuo labiau taikomos senosioms.„Amatų ir privačios funkcijos“.

Pagarba. Slidinėjo ne tam, kad apgaudinėtų konstantą (tobto skaičių) kaip pinigų sumą ir kaip pastovų daugiklį! Ties vipadku dodanku її prarandama iki nulio, o vienkartinio daugiklio atveju laimima kaltas dėl senojo ženklo. Tse tipiška pomilka, kaip vystytis vyresniųjų vivchennya burbuolės stadijoje, ala pasaulyje atgimsta tiek pat vieno-dviejų aukštų užpakaliukų vidurio mokinys tsyu, atsiprašau, kad ir kaip sunku būtų.

O kai atskiriate privataus kūrimą, turite dodanoką u"v kuriame u- skaičius, pavyzdžiui, 2 arba 5, taigi tai yra konstanta, tada prarastas skaičius bus lygus nuliui, bet vis tiek bus nulis (šio tipo ekranas užpakaliukui yra 10).

Іnsha dažnas atleidimas- elementarių lankstymo funkcijų mechaninis sprendimas kaip paprastos paprastos funkcijos. Tomas lieso lankstymo funkcija priskirtas straipsniui. Šiek tiek to, ką galima lengvai sužinoti ir prarasti paprastos funkcijos.

Pakeliui neapsieisite be viraz peržiūros. Visų jų kritikus galite pamatyti prie naujų svetainės langų Pasidaryk pats su žingsneliais ir šaknimisі Pasidaryk pats su trupmenomis .

Yaksho Vi shukte senųjų trupmenų sprendimą žingsniais ir šaknimis, tobto, jei funkcija ma viglyad nachebto , tada eikite į užimtą „Eiti į trupmenų sumą žingsniais iki šaknų“.

Na, priešais jus yra nachebto , tada jūs esate užimtas „Vyrobni paprastos trigonometrinės funkcijos“.

Pokrokovi užpakalis - kaip žinoti, kad eisiu

atsargos 3.Žinokite prarastą funkciją

Sprendimas. Pirmoji funkcijos virazo dalis: visas virazas vaizduojamas tvir, kaip ir daugikliai - sumi, iš kitos, vienas iš ankstesniųjų turi atkeršyti pastoviam daugikliui. Galioja griežta būtybės atskyrimo taisyklė: sukurkite dvi originalo funkcijas:

Atsižvelgiant į nustatytą sumi diferenciacijos taisyklę: prarandama ankstesnės senųjų cich funkcijų algebros sumos algebrinių funkcijų suma. Mūsų vipad sumos odoje turi dar vieną priedą su minuso ženklu. Odos gaminių atveju bachimo ir nepriklausomas pokytis, kurie prarandami kai kuriuose kelio koeficientuose, ir konstanta (skaičius), tokiuose keliuose prarandami kaip nulis. Otzhe, "ix" keičiame į vieną, o minus 5 - į nulį. Kitame viraze "ix" dauginamas iš 2, taigi du kartus dauginami iš to paties vieneto, kaip ir aš eisiu į "ix". Otrimuєmo šias senesnių reikšmes:

Būtina, kad protas prarastų visas funkcijas:

Ir galima susitaikyti su problemos sprendimo užduotimi dienos pabaigoje.

atsargos 4.Žinokite prarastą funkciją

Sprendimas. Iš mūsų būtina žinoti privataus dingimą. Yra fiksuota dalies diferencijavimo formulė: dviejų funkcijų dalys prarandamos kelio trupmenai, є skaičiaus skaičius yra skaičiaus skaičiaus skaičius, o skaičius yra skaičiaus kvadratas. skaičių skaičius. Otrimuєmo:

Pereisiu prie skaičiaus daugiklio, o aš jau žinojau jį užpakaliuke 2. Nepamirškite, kad tai tas pats, kad kitas srauto sandėlyje esantis daugiklis imamas su minuso ženklu:

Yaksho Vi shukate tokių pastatų peržiūrą, tiems, kam reikia žinoti, aš prarasiu savo funkcijas, de facto krūvą šaknų ir laiptelių, kaip pvz. , tada maloniai paprašykite užimtų „Virobnos sumi frakcijos žingsniais ir šaknimis“ .

Ar norėtumėte daugiau sužinoti apie prarastus sinusus, kosinusus, tangentus ir inshi trigonometrinės funkcijos, tobto, jei funkcija maє viglyad nachebto , tada tavo pamoka "Virobni paprastos trigonometrinės funkcijos" .

5 užpakalis.Žinokite prarastą funkciją

Sprendimas. Visoje bachimo tviro, kurio vienas iš daugiklių yra nepriklausomo žieminio kvadratinė šaknis, funkcijoje, senųjų lentelėse buvo atpažinti senieji. Pagal atskirties nuo būtybės taisyklę pasenusios kvadratinės šaknies lentelės reikšmė bus atpažįstama:

Užduočių sprendimą galite peržiūrėti paskutiniam internetinis skaičiuotuvas .

6 užpakalis.Žinokite prarastą funkciją

Sprendimas. Funkcija yra bachimo privati ​​ir yra kvadratinė šaknis iš nepriklausomo kraštovaizdžio. Pagal eilinio diferenciacijos taisyklę kartojo, kad įstrigo į užpakalį 4, kad bus atpažinta pasenusios kvadratinės šaknies lentelės reikšmė:

Schob nukratykite skaitmens trupmeną, padauginkite skaičių ir vardiklį.

Sulankstomos peržiūros funkcija, kuri priklauso nuo sulankstymo funkcijos. Kadangi funkcija yra formos y = sin x - (2 - 3) a r c t g x x 5 7 x 10 - 17 x 3 + x - 11, tada jos negalima sulenkti į vaizdą kaip y = sin 2 x.

Straipsnis parodys supratimą apie sulankstymo funkciją ir išvaizdą. Pataisyta pagal formules znakhozhennya pohіdnoї іf užpakaliukai pakilo ties visnovku. Senųjų lentelių sąstingis ir diferenciacijos taisyklės gali būti keičiamos, keičiant valandas senosioms.

Pagrindinės vertybės

Verslo vertė 1

Lankstymo funkcija naudojama tokiai funkcijai, nes argumentas taip pat yra funkcija.

Tai reiškia tse taip: f (g (x)). Mum, kad funkcija g (x) dalyvauja argumente f (g (x)).

Verslo vertė 2

Be to, funkcija yra f ir yra kotangento funkcija, taigi g (x) = ln x yra visa natūraliojo logaritmo funkcija. Pripažįstame, kad lankstymo funkcija f (g (x)) gali būti parašyta kaip arctan (lnx). Kad funkcija f, kuri yra 4 žingsnių funkcija, de g (x) = x 2 + 2 x - 3 būtų naudojama kaip visa racionali funkcija, galime paneigti, kad f (g (x)) = (x 2 + 2 x - 3) 4 .

Akivaizdu, kad g (x) gali būti sulankstomas. Iš užpakalio y = sin 2 x + 1 x 3 - 5 matyti, kad g maє reikšmė kubinė šaknis s trupmena. Daniy viraz gali būti apibrėžtas kaip y = f (f 1 (f 2 (x))). Žvaigždės yra mamo, f yra sinuso funkcija, o f 1 yra funkcija, kurią galima paversti kvadratine šaknimi, f 2 (x) = 2 x + 1 x 3 - 5 yra racionalioji funkcija.

Verslo vertė 3

Įnašo žingsnis turi būti natūralusis skaičius ir rašomas kaip y = f (f 1 (f 2 (f 3 (... (F n (x))))))))).

Verslo vertė 4

Funkcijos sudėties supratimas turėtų būti nustatomas atsižvelgiant į indėlių į protą skaičių. Pirmą kartą svarstoma liesos lankstymo funkcijos pažinimo formulė

(f (g (x)))) "= f" (g (x)) g "(x)

Užsidėk

1 užpakalis

Žinokite prarastą lankstymo funkciją forma y = (2 x + 1) 2.

Sprendimas

Už plovimo aišku, kad f yra kvadrato funkcija, o g (x) = 2 x + 1 naudojama tiesinei funkcijai.

Yra labai paplitusi lankstymo funkcijos formulė, kurią galima užrašyti:

f "(g (x)) = ((g (x)) 2)" = 2 · (g (x)) 2 - 1 = 2 · g (x) = 2 · (2 ​​× + 1); g "(x) = (2 x + 1)" = (2 x) "+ 1" = 2 x "+ 0 = 2 1 x 1 - 1 = 2 ⇒ (f (g (x))) "= f " (g (x)) g "(x) = 2 (2 x + 1) 2 = 8 x + 4

Būtina pažinti pasiklydusį, atleidžiant išorinį funkcijos vaizdą. Otrimuєmo:

y = (2 x + 1) 2 = 4 x 2 + 4 x + 1

Zvidsi maєmo, scho

y "= (4 x 2 + 4 x + 1)" = (4 x 2) "+ (4 x)" + 1 "= 4 · (x 2)" + 4 · (x) "+ 0 = = 4 2 x 2 – 1 + 4 1 x 1 – 1 = 8 x + 4

Rezultatai buvo vertinami balais.

Žiūrint šio tipo augalus, svarbu suprasti de roztashovuvatyuvati formos f і g (x) funkciją.

2 užpakalis

Slyskite, kad sužinotumėte senąsias formos y = sin 2 x ir y = sin x 2 lankstymo funkcijas.

Sprendimas

Pirmasis, kuris užrašo funkciją, yra redukcija, bet f yra kvadrato funkcija, o g (x) yra sinuso funkcija. Todi otrimaєmo, scho

y "= (sin 2 x)" = 2 sin 2 - 1 x (sin x) "= 2 sin x cos x

Kitas žymėjimas rodo, kad f yra sinusinė funkcija, o g (x) = x 2 yra valstybinė funkcija... Žvidsy vipliv

y "= (sin x 2)" = cos (x 2) (x 2) "= cos (x 2) 2 x 2 - 1 = 2 x cos (x 2)

Paprastos y = f formulė (f 1 (f 2 (f 3 (... (Fn (x)))))))) parašyta kaip y "= f" (f 1 (f 2 (f 3 ()) . .) fn (x)))))) f 1 "(f 2 (f 3 (... (fn (x)))))) f 2" (f 3 (... (fn ( x)) )))) ... ... · F n "(x)

3 užpakalis

Žinokite prarastąją funkciją y = sin (ln 3 a r c t g (2 x)).

Sprendimas

Daniškas užpakalis parodys įrašo sulankstymą ir rozetavimo funkcijų žymėjimą. Todi y = f (f 1 (f 2 (f 3 (f 4 (x)))))), de f, f 1, f 2, f 3, f 4 (x) yra sinuso funkcija, 3 žingsniai, logaritmo funkcija yra bazė e, funkcija yra arctangentas ir linija.

3 lankstymo funkcijos reikšmės formulės maєmo, scho

y "= f" (f 1 (f 2 (f 3 (f 4 (x))))) f 1 "(f 2 (f 3 (f 4 (x))))) f 2" ( f 3 ( f 4 (x))) f 3 "(f 4 (x)) f 4" (x)

Otrimuєmo, kaip zinoti

1. f "(f 1 (f 2 (f 3 (f 4 (x))))), nes sinusas pagrobtas pagal senesnių lenteles, tood f" (f 1 (f 2 (f 3 (f 4 ()) x))))) ) = cos (ln 3 arctan (2 x)).
2. f 1 "(f 2 (f 3 (f 4 (x))))) Aš imsiu būsenos funkciją, taigi f 1" (f 2 (f 3 (f 4 (x)))) = 3 ln 3 - 1 arctan (2 x) = 3 ln 2 arctan (2 x).
3. f 2 "(f 3 (f 4 (x))) yra logaritminis, taigi f 2" (f 3 (f 4 (x))) = 1 a r c t g (2 x).
4. f 3 "(f 4 (x)) kaip senesnis arctangentas, toodi f 3" (f 4 (x)) = 1 1 + (2 x) 2 = 1 1 + 4 x 2.
5. Su žinomu blogu f 4 (x) = 2 x mirtis 2, jei blogas ženklas dėl blogos statistinės formulės su rodikliu, kuris yra brangus 1 iki f 4 "(x) = (2 x)" = 2 x "= 2 · 1 x 1 – 1 = 2.

Tarpinių rezultatų, kurie bus pripažinti, integravimas,

y "= f" (f 1 (f 2 (f 3 (f 4 (x))))) f 1 "(f 2 (f 3 (f 4 (x))))) f 2" ( f 3 ( f 4 (x))) f 3 "(f 4 (x)) f 4" (x) = = cos (ln 3 arctan (2 x)) 3 ln 2 arctan (2 x) 1 arctan (2 x) 1 1 + 4 x 2 2 = = 6 cos (ln 3 arctan (2 x)) ln 2 arctan (2 x) arctan (2 x) (1 + 4 x 2)

Tokių nagadu matrioshka funkcijų pasirinkimas. Nesitikima laikytis diferenciacijos taisyklių akivaizdus viglyadі papildomoms senesnių lentelių. Dažniausiai reikia nustatyti senų lankstymo funkcijų išmanymo formulę.

Pažiūrėkite, kaip atrodo sulankstomos lankstymo funkcijos. Esant aiškiam vystymosi jausmui, senatvės pažinimas yra ypač lengvas.

4 užpakalis

Būtina pažvelgti į tokio užpakalio taikymą. Kadangi tai formos y = t g 2 x + 3 t g x + 1 funkcija, tai galima žiūrėti į sulankstytą g (x) = t g x, f (g) = g 2 + 3 g + 1 formą. Akivaizdu, kad būtina rasti sulankstomo bjaurus formulę:

f "(g (x)) = (g 2 (x) + 3 g (x) + 1)" = (g 2 (x)) "+ (3 g (x))" + 1 "= = 2 · g 2 - 1 (x) + 3 · g "(x) + 0 = 2 g (x) + 3 · 1 · g 1 - 1 (x) = = 2 g (x) + 3 = 2 tgx + 3; g "(x) = (tgx)" = 1 cos 2 x ⇒ y "= (f (g (x)))" = f "(g (x)) g" (x) = (2 tgx + 3 ) 1 cos 2 x = 2 tgx + 3 cos 2 x

Formos y = t g x 2 + 3 t g x + 1 funkcija netelpa į sulankstomą, sumos t g x 2 3 t g x і 1 fragmentus. Tačiau t g x 2 telpa į lankstymo funkciją, tada būsenos funkciją galime priimti kaip g (x) = x 2 і f є liestinės funkciją. Už visą skirtumą krepšiui. Otrimuєmo, scho

y "= (tgx 2 + 3 tgx + 1)" = (tgx 2) "+ (3 tgx)" + 1 "= = (tgx 2)" + 3 · (tgx) "+ 0 = (tgx 2)" + 3 cos 2 x

Mes pereiname prie žinomos elementarios lankstymo funkcijos (t g x 2) ":

f "(g (x)) = (deg (g (x)))" = 1 cos 2 g (x) = 1 cos 2 (x 2) g "(x) = (x 2)" = 2 x 2 - 1 = 2 x ⇒ (tgx 2) "= f" (g (x)) g "(x) = 2 x cos 2 (x 2)

Galime atpažinti, kad y "= (t g x 2 + 3 t g x + 1)" = (t g x 2) "+ 3 cos 2 x = 2 x cos 2 (x 2) + 3 cos 2 x

Lankstymo funkcijos gali būti įtrauktos prieš sulankstymo funkcijų sandėlį, o pačios sulankstymo funkcijos gali būti sulankstomos.

5 užpakalis

Programą galima lengvai suskleisti tokia forma: y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x (x 2 + 1)

Šią funkciją galima pavaizduoti vaizdu y = f (g (x)), o tai reiškia, kad f yra logaritmo funkcija 3 poaibyje, o g (x) gali būti naudojama kaip dviejų h (x) formos funkcijų suma ) = x 2 + 3 cos 3 (2 x + 1) + 7 ex 2 + 3 3 і k (x) = ln 2 x (x 2 + 1). Akivaizdu, kad y = f (h (x) + k (x)).

Funkcija h (x) suprantama. Kaina l (x) = x 2 + 3 cos 3 (2 x + 1) + 7 iki m (x) = e x 2 + 3 3

Mahmo, l (x) = x 2 + 3 cos 2 (2 x + 1) + 7 = n (x) + p (x) є dviejų funkcijų suma n (x) = x 2 + 7 ir p (x) ) = 3 cos 3 (2 x + 1), de p (x) = 3 p 1 (p 2 (p 3 (x))) yra lankstymo funkcija su skaitine funkcija 3, o p 1 yra sumažinimo iki kubas, p 2 kosinuso funkcija, p 3 (x) = 2 x + 1 yra tiesinė funkcija.

Jei m (x) = ex 2 + 3 3 = q (x) + r (x) є dviejų funkcijų suma q (x) = ex 2 і r (x) = 3 3 de q (x) = q 1 (q 2 (x)) yra lankstymo funkcija, q 1 yra eksponentinė funkcija, q 2 (x) = x 2 yra būsenos funkcija.

Matyti, kad h (x) = l (x) m (x) = n (x) + p (x) q (x) + r (x) = n (x) + 3 p 1 (p 2 () p 3 (x))) q 1 (q 2 (x)) + r (x)

Einant į formos k (x) = ln 2 x (x 2 + 1) = s (x) 1 (s 2 (x)) virazą su visu racionaliu t (x) = x 2 + 1, de s 1 yra kvadrato funkcija, o s 2 (x) = ln x yra logaritminis pagrindas e.

Atrodo kaip mirktelėjimas, todėl galite pamatyti k (x) = s (x) t (x) = s 1 (s 2 (x)) t (x).

Todi otrimaєmo, scho

y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 ex 2 + 3 3 + ln 2 x (x 2 + 1) = = fn (x) + 3 p 1 (p 2 (p 3 () x))) q 1 (q 2 (x)) = r (x) + s 1 (s 2 (x)) t (x)

Už funkcijos struktūrų tapo aišku, kad reikia pataisyti formules, kad būtų lengviau pritaikyti šią diferenciaciją. Norint pažinti kitus pastatus ir suprasti jų perdavimą, reikia atsigręžti į funkcijos diferenciacijos tašką, norint sužinoti linksmiausią.

Yaksho Vi tekste pažymėjo atleidimą, būk žiburėlis, pamatyk ir natisnit Ctrl + Enter

Pirmoji teorema apie prarastą lankstymo funkciją, kurios formulė yra tokia:

Eikite 1) funkcija $ u = \ varphi (x) $ gali būti naudojama norint gauti $ u_ (x) "= \ varphi" (x_0) $; 2) funkcija $ y = f (u) $ gali būti naudojama tuose pačiuose taškuose $ u_0 = \ varphi (x_0) $ reikės $ y_ (u) "= f" (u) $. Todi sulankstoma funkcija $ y = f \ left (\ varphi (x) \ right) $ spėjamuose taškuose, aš taip pat prarasiu tą patį, pridėsiu keletą senesnių funkcijų $ f (u) $ i $ \ varphi (x) $ :

$$ \ left (f (\ varphi (x)) \ right) "= f_ (u)" \ left (\ varphi (x_0) \ right) \ cdot \ varphi "(x_0) $$

Tačiau didesniu trumpu užrašu: $ y_ (x) "= y_ (u)" \ cdot u_ (x) "$.

To paties skirstinio užpakaliuose visos funkcijos gali būti matomos $ y = f (x) $ forma (kad būtų matoma tik viena keičiama $ x $ funkcija). Matyt, visos akcijos turi $ y "$ tackle $ x $ pokytį.

Prie užpakalių Nr. 1, Nr. 2 ir Nr. 3 buvo atliktas zakhozhennya pohіdnoї sulankstymo funkcijų ataskaitų procesas. Senesnių ir protingesnių lentelių didesnio aiškumo ženklų priedas Nr.

Bazhano pislya vivchennya medžiaga atsargose Nr. 1-3 pereikite prie nepriklausomo atsargų Nr. 5, Nr. 6 ir Nr. 7 sprendimo. Pritaikykite Nr. 5, Nr. 6 ir Nr. 7 trumpam sprendimui, kad skaitytojas galėtų persvarstyti savo rezultato teisingumą.

Užpakalis numeris 1

Žinokite prarastą funkciją $ y = e ^ (\ cos x) $.

Turime žinoti prarastą lankstymo funkciją $ y "$. Virpesiai $ y = e ^ (\ cos x) $, tada $ y" = \ kairė (e ^ (\ cos x) \ dešinė) "$. kairė (e ^ (\ cos x) \ right) "$ vikor formulė # 6 iš senesnių lentelių. Na, beje, reikalinga formulė # 6, bet mūsų atveju $ u = \ cos x $. Tolesnis lauko sprendimas banaliai įdiegus formulę №6 viraz $ \ cos x $ pakeis $ u $:

$$ y "= \ left (e ^ (\ cos x) \ right)" = e ^ (\ cos x) \ cdot (\ cos x) "\ tag (1.1) $$

Dabar reikia žinoti viraz $ (\ cos x) "$ reikšmę. Pažįstu žvėrį į senesnių lentelę, iš jo parinkta formulė Nr. 10. Galite pateikti $ u = x $ už formulė Nr. 10, bet: $ (\ cos x)" = - \ sin x \ cdot x "$. Dabar (1.1) paritetas tęsiamas, pridedant tokį rezultatą:

$$ y "= \ kairėje (e ^ (\ cos x) \ dešinėje)" = e ^ (\ cos x) \ cdot (\ cos x) "= e ^ (\ cos x) \ cdot (- \ sin x \ cdot x ") \ žyma (1.2) $$

Virpesiai $ x "= 1 $, tada paritetas (1.2) tęsiamas:

$$ y "= \ kairėje (e ^ (\ cos x) \ dešinėje)" = e ^ (\ cos x) \ cdot (\ cos x) "= e ^ (\ cos x) \ cdot (- \ sin x \ cdot x ") = e ^ (\ cos x) \ cdot (- \ sin x \ cdot 1) = - \ sin x \ cdot e ^ (\ cos x) \ žyma (1.3) $$

Otzhe, pagal (1.3), maєmo: $ y "= - \ sin x \ cdot e ^ (\ cos x) $. 1.3) Otzhe, lankstymo funkcija buvo prarasta, ji buvo atimta įrašymas.

Žiūrėti: $ y "= - \ sin x \ cdot e ^ (\ cos x) $.

Užpakalis numeris 2

Žinokite prarastą funkciją $ y = 9 \ cdot \ arctg ^ (12) (4 \ cdot \ ln x) $.

Turime suskaičiuoti prarastus $ y "= \ left (9 \ cdot \ arctg ^ (12) (4 \ cdot \ ln x) \ right)" $. Visiškai aišku, kad dėl blogo ženklo galima kaltinti konstantą (ty skaičių 9):

$$ y "= \ left (9 \ cdot \ arctg ^ (12) (4 \ cdot \ ln x) \ right)" = 9 \ cdot \ left (\ arctg ^ (12) (4 \ cdot \ ln x) \ dešinėje) "\ žyma (2.1) $$

Dabar viral, $ \ left (\ arctg ^ (12) (4 \ cdot \ ln x) \ right) "$. Jei norite vibruoti, man lengviau reikės formulės iš senų kaušų lentelių, aš padarysiu Pateikite virazą, kaip žiūrėti tokiame vaizde: $ \ left (\ left (\ arctg (4 \ cdot \ ln x) \ right) ^ (12) \ right) "$. Dabar aišku, kad reikia vikoristovuvati formulę Nr.2, tobto. $ \ kairėje (u ^ \ alfa \ dešinėje) "= \ alfa \ cdot u ^ (\ alfa-1) \ cdot u" $. Formulė pavaizduota $ u = \ arctg (4 \ cdot \ ln x) $ і $ \ alfa = 12 $:

Papildoma lygybė (2.1) atimama iš rezultato, be to:

$$ y "= \ left (9 \ cdot \ arctg ^ (12) (4 \ cdot \ ln x) \ right)" = 9 \ cdot \ left (\ arctg ^ (12) (4 \ cdot \ ln x) \ right) "= 108 \ cdot \ left (\ arctg (4 \ cdot \ ln x) \ right) ^ (11) \ cdot (\ arctg (4 \ cdot \ ln x))" \ žyma (2.2) $$

Šioje situacijoje dažnai leidžiama atleisti, jei pirmą kartą pasirenkate formulę $ (\ arctg \; u) "= \ frac (1) (1 + u ^ 2) \ cdot u" $ pakeiskite formules $ \ kairėje (u ^ \ alfa \ dešinėje) "= \ alfa \ cdot u ^ (\ alfa-1) \ cdot u" $. Dešinėje pirmasis yra kaltas dėl pradinės funkcijos. Pažvelkite į tai, nes pati funkcija bus naudinga sukant $ \ arctg ^ (12) (4 \ cdot 5 ^ x) $, pažiūrėkite, ar naudojate reikšmę $ \ arctg ^ (12) (4 \ cdot 5 ^ x) $, kurio vertė yra $ x $. Naudokite nedidelį $ 5 ^ x $ reikšmių pasirinkimą, tada padauginkite rezultatą iš 4, iškirpdami $ 4 \ cdot 5 ^ x $. Nuo šiol arctangentas paimamas iš rezultato, pašalinus $ arctg (4cdot 5 ^ x) $. Tada skaičių galima sumažinti iki dvylikos žingsnių, kurie gali būti pateikti kaip $ arctg (12) (4 cdot 5 x) $. Stop dia - tobto. 12 žingsnyje esantis pastatas atliks puikią funkciją. Pirmas dalykas, kurį reikia padaryti, yra sutvarkyti seną, bet jį sulaužė noras (2.2).

Dabar reikia žinoti $ (\ arctg (4 \ cdot \ ln x)) "$. Vikoristo formulė Nr. 19 senesnių lentelių, įdėjus į ją $ ​​u = 4 \ cdot \ ln x $:

$$ (\ arctg (4 \ cdot \ ln x)) "= \ frac (1) (1+ (4 \ cdot \ ln x) ^ 2) \ cdot (4 \ cdot \ ln x)" $$

Triletus galima lengvai pašalinti iš virazo ir naudojant $ (4 \ cdot \ nn x) ^ 2 = 4 ^ 2 \ cdot (\ ln x) ^ 2 = 16 \ cdot \ ln ^ 2 x $.

$$ (\ arctg (4 \ cdot \ ln x)) "= \ frac (1) (1+ (4 \ cdot \ ln x) ^ 2) \ cdot (4 \ cdot \ ln x)" = \ frac ( 1) (1 + 16 \ cdot \ ln ^ 2 x) \ cdot (4 \ cdot \ ln x) "$$

Lygybė (2.2) dabar yra tokia:

$$ y "= \ left (9 \ cdot \ arctg ^ (12) (4 \ cdot \ ln x) \ right)" = 9 \ cdot \ left (\ arctg ^ (12) (4 \ cdot \ ln x) \ dešinė) "= \\ = 108 \ cdot \ left (\ arctg (4 \ cdot \ ln x) \ right) ^ (11) \ cdot (\ arctg (4 \ cdot \ ln x))" = 108 \ cdot \ kairėje (\ arctg (4 \ cdot \ ln x) \ dešinėje) ^ (11) \ cdot \ frac (1) (1 + 16 \ cdot \ ln ^ 2 x) \ cdot (4 \ cdot \ ln x) " \ žyma (2.3) $$

Jau per vėlu žinoti $ (4 \ cdot \ ln x) "$. Taigi blogo ženklo konstanta (tobto 4): $ (4 \ cdot \ ln x)" = 4 \ cdot (\ ln x) "$ . $ (\ ln x) "$ vikoristymo formulė №8, įtraukiant į ją $ ​​u = x $: $ (\ ln x)" = \ frac (1) (x) \ cdot x "$. Oskilki $ x "= 1 $, tada $ (\ ln x)" = \ frac (1) (x) \ cdot x "= \ frac (1) (x) \ cdot 1 = \ frac (1) (x) $. Pateikę rezultato atmetimą į (2.3) formulę, galime padaryti išvadą:

$$ y "= \ left (9 \ cdot \ arctg ^ (12) (4 \ cdot \ ln x) \ right)" = 9 \ cdot \ left (\ arctg ^ (12) (4 \ cdot \ ln x) \ dešinė) "= \\ = 108 \ cdot \ left (\ arctg (4 \ cdot \ ln x) \ right) ^ (11) \ cdot (\ arctg (4 \ cdot \ ln x))" = 108 \ cdot \ kairėje (\ arctg (4 \ cdot \ ln x) \ dešinėje) ^ (11) \ cdot \ frac (1) (1 + 16 \ cdot \ ln ^ 2 x) \ cdot (4 \ cdot \ ln x) " = \\ = 108 \ cdot \ left (\ arctg (4 \ cdot \ ln x) \ right) ^ (11) \ cdot \ frac (1) (1 + 16 \ cdot \ ln ^ 2 x) \ cdot 4 \ cdot \ frac (1) (x) = 432 \ cdot \ frac (\ arctg ^ (11) (4 \ cdot \ ln x)) (x \ cdot (1 + 16 \ cdot \ ln ^ 2 x)). $

Spėju, kad lankstymo funkcija dažniausiai yra vienoje eilėje – kaip parašyta paskutiniame rimnosti. Tai yra, įforminant standartinius projektus ar valdymo robotus, nereikia taip detaliai aprašyti sprendimo.

Žiūrėti: $ y "= 432 \ cdot \ frac (\ arctg ^ (11) (4 \ cdot \ ln x)) (x \ cdot (1 + 16 \ cdot \ ln ^ 2 x)) $.

Užpakalis Nr.3

Žinokite $ y "$ funkcijas $ y = \ sqrt (\ sin ^ 3 (5 \ cdot9 ^ x)) $.

Trijų burbuliukų atveju pakeiskite funkciją $ y $, užfiksuodami žingsninio rodinio radikalą (šaknį): $ y = \ sqrt (\ sin ^ 3 (5 \ cdot9 ^ x)) = \ left (\ sin () 5 \ cdot 9 ^ x) \ dešinė) ^ (\ frac (3) (7)) $. Dabar tai prasidės iki pirmųjų dienų. Oskilki $ y = \ left (\ sin (5 \ cdot 9 ^ x) \ right) ^ (\ frac (3) (7)) $, tada:

$$ y "= \ left (\ left (\ sin (5 \ cdot 9 ^ x) \ right) ^ (\ frac (3) (7)) \ right)" \ žyma (3.1) $$

Viktoro formulė Nr. 2 iš senesnių lentelių, įdėjus į ją $ ​​u = \ sin (5 \ cdot 9 ^ x) $ і $ \ alfa = \ frac (3) (7) $:

$$ \ left (\ left (\ sin (5 \ cdot 9 ^ x) \ right) ^ (\ frac (3) (7)) \ right) "= \ frac (3) (7) \ cdot \ left ( \ sin (5 \ cdot 9 ^ x) \ dešinė) ^ (\ frac (3) (7) -1) (\ sin (5 \ cdot 9 ^ x)) "= \ frac (3) (7) \ cdot \ left (\ sin (5 \ cdot 9 ^ x) \ right) ^ (- \ frac (4) (7)) (\ sin (5 \ cdot 9 ^ x)) "$$

Nuolat lygus (3.1), rezultatas yra toks:

$$ y "= \ kairė (\ kairė (\ sin (5 \ cdot 9 ^ x) \ dešinė) ^ (\ frac (3) (7)) \ dešinė)" = \ frac (3) (7) \ cdot \ kairėje (\ sin (5 \ cdot 9 ^ x) \ dešinėje) ^ (- \ frac (4) (7)) (\ sin (5 \ cdot 9 ^ x)) "\ žyma (3.2) $$

Dabar reikia žinoti $ (\ sin (5 \ cdot 9 ^ x)) "$. Vikoristovuєmo visai formulei Nr. 9 iš senesnių lentelių, įdėjus į ją $ ​​u = 5 \ cdot 9 ^ x $:

$$ (\ sin (5 \ cdot 9 ^ x)) "= \ cos (5 \ cdot 9 ^ x) \ cdot (5 \ cdot 9 ^ x)" $$

Patobulinę paritetą (3,2), paneigkime rezultatą:

$$ y "= \ kairė (\ kairė (\ sin (5 \ cdot 9 ^ x) \ dešinė) ^ (\ frac (3) (7)) \ dešinė)" = \ frac (3) (7) \ cdot \ left (\ sin (5 \ cdot 9 ^ x) \ right) ^ (- \ frac (4) (7)) (\ sin (5 \ cdot 9 ^ x)) "= \\ = \ frac (3) (7) \ cdot \ left (\ sin (5 \ cdot 9 ^ x) \ right) ^ (- \ frac (4) (7)) \ cos (5 \ cdot 9 ^ x) \ cdot (5 \ cdot 9 ^ x) "\ žyma (3.3) $$

Jau buvo per vėlu žinoti $ (5 \ cdot 9 ^ x) "$. Burbuolei mums reikia konstantos (skaičiaus $ 5 $) blogam ženklui, taigi $ (5 \ cdot 9 ^ x)" = 5 \ cdot (9 ^ x) "$. Žinomam senam $ (9 ^ x) "$ naudosite senųjų lentelių formulę Nr. 5, jai pateikę $ a = 9 $ і $ u = x $: $ (9 ^ x)" = 9 ^ x \ cdot \ ln9 \ cdot x "$. Virpesiai $ x "= 1 $, tada $ (9 ^ x)" = 9 ^ x \ cdot \ ln9 \ cdot x "= 9 ^ x \ cdot \ ln9 $. Dabar galime tęsti lygybę (3.3):

$$ y "= \ kairė (\ kairė (\ sin (5 \ cdot 9 ^ x) \ dešinė) ^ (\ frac (3) (7)) \ dešinė)" = \ frac (3) (7) \ cdot \ left (\ sin (5 \ cdot 9 ^ x) \ right) ^ (- \ frac (4) (7)) (\ sin (5 \ cdot 9 ^ x)) "= \\ = \ frac (3) (7) \ cdot \ left (\ sin (5 \ cdot 9 ^ x) \ right) ^ (- \ frac (4) (7)) \ cos (5 \ cdot 9 ^ x) \ cdot (5 \ cdot 9 ^ x) "= \ frac (3) (7) \ cdot \ left (\ sin (5 \ cdot 9 ^ x) \ dešinė) ^ (- \ frac (4) (7)) \ cos (5 \ cdot 9 ^ x) \ cdot 5 \ cdot 9 ^ x \ cdot \ ln9 = \\ = \ frac (15 \ cdot \ ln 9) (7) \ cdot \ left (\ sin (5 \ cdot 9 ^ x) \ dešinė) ^ (- \ frac (4) (7)) \ cdot \ cos (5 \ cdot 9 ^ x) \ cdot 9 ^ x. $$

Galite dar kartą pereiti nuo žingsnių prie radikalų (būti šaknimis), įrašydami $ \ left (\ sin (5 \ cdot 9 ^ x) \ right) ^ (- \ frac (4) (7)) $ žiūrovas $ \ frac (1 ) (\ kairėje (\ sin (5 \ cdot 9 ^ x) \ dešinėje) ^ (\ frac (4) (7))) = \ frac (1) (\ sqrt (\ sin ^ 4 (5 \) cdot 9 ^ x))) $. Todi bus parašyta tokia forma:

$$ y "= \ frac (15 \ cdot \ ln 9) (7) \ cdot \ left (\ sin (5 \ cdot 9 ^ x) \ dešinė) ^ (- \ frac (4) (7)) \ cdot \ cos (5 \ cdot 9 ^ x) \ cdot 9 ^ x = \ frac (15 \ cdot \ ln 9) (7) \ cdot \ frac (\ cos (5 \ cdot 9 ^ x) \ cdot 9 ^ x) (\ sqrt (\ sin ^ 4 (5 \ cdot 9 ^ x))). $$

Žiūrėti: $ y "= \ frac (15 \ cdot \ ln 9) (7) \ cdot \ frac (\ cos (5 \ cdot 9 ^ x) \ cdot 9 ^ x) (\ sqrt (\ sin ^ 4 (5 \) ) cdot 9 ^ x))) $.

Užpakalis Nr.4

Parodykite, kad senesnės є okremiy lentelės formulės Nr. 3 ir Nr. 4 lentelės formulės Nr. 2.

Senesnių lentelių formulė # 2 turi tą pačią funkciją $ u ^ \ alpha $. Pateikiame $ \ alfa = -1 $ formulei Nr. 2, galime atpažinti:

$$ (u ^ (- 1)) "= - 1 \ cdot u ^ (- 1-1) \ cdot u" = - u ^ (- 2) \ cdot u "\ žyma (4.1) $$

Virpesiai $ u ^ (- 1) = \ frac (1) (u) $ і $ u ^ (- 2) = \ frac (1) (u ^ 2) $, tada lygybę (4.1) galima perrašyti taip: $ \ left (\ frac (1) (u) \ right) "= - \ frac (1) (u ^ 2) \ cdot u" $. Tse і є formulė Nr.3 senesnių lentelių.

Pažįstu žvėris iki senesnių lentelių formulės Nr.2. Išplečiamai $ \ alfa = \ frac (1) (2) $:

$$ \ left (u ^ (\ frac (1) (2)) \ right) "= \ frac (1) (2) \ cdot u ^ (\ frac (1) (2) -1) \ cdot u" = \ frac (1) (2) u ^ (- \ frac (1) (2)) \ cdot u "\ žyma (4.2) $$

Oskilki $ u ^ (\ frac (1) (2)) = \ sqrt (u) $ і $ u ^ (- \ frac (1) (2)) = \ frac (1) (u ^ (\ frac (1) ) (2))) = \ frac (1) (\ sqrt (u)) $, tada paritetą (4.2) galima perrašyti tokiu būdu:

$$ (\ sqrt (u)) "= \ frac (1) (2) \ cdot \ frac (1) (\ sqrt (u)) \ cdot u" = \ frac (1) (2 \ kvadratas (u) ) \ cdot u "$$

Otrimana paritetas $ (sqrt (u)) "= \ frac (1) (2sqrt (u)) cdot u" $ і formulė Nr. 4 senesnių lentelių. Jakų bachitas, senesnių formulės Nr. 3 ir Nr. 4 lentelės nuo formulės Nr. 2 pereina prie $ alfa $ nustatymo.