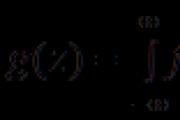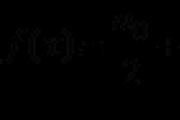Sistemi logičkih jednakosti. Tema lekcije: "Sistemi logičkih jednakosti"

04.04.2021

Ovaj materijal treba da bude predstavljen kao prezentacija metoda za razvoj logičkih poravnanja i sistema logičkih poravnanja na čelu B15 (br. 23, 2015) ÊDÍ iz ínformatike. Čini se da je zadatak jedan od najkomplikovanijih među radnicima EDI-ja. Prezentacija može biti otrcana za sat lekcija na temu "Logika" u specijaliziranoj nastavi, kao i za sat pripreme prije zadatka EDI.

Prednost:

Pogled sprijeda:

Kako biste unaprijed ubrzali prezentaciju, kreirajte vlastiti Google Post i pogledajte prije: https://accounts.google.com

Naslovi prije slajdova:

Vishnevska M.P., MAOU "Gimnazija br. 3" 18. novembra 2013, grad Saratov

Zadatak B15 - jedan od najnaprednijih u EDI informatike! Revíryayutsya vmínnya: vírazi vírazi, scho da osveti logične promjene; opisati značenje logičkih promjena uz pomoć prirodnog jezika, uz određene zadatke prikupljanja logičkih promjena u istini; pídrakhovuvat kílkíst dvíykovyh naborív, yakí vídpovídat zadovannymi umov. Zgodnije, jer nema formalnih pravila, kao da je potrebno, potrebno je pogoditi.

Bez čega ne!

Pametna konjunkcija: A /\ B , A  B , AB , A &B, A i B disjunkcija: A / B , A + B , A | B , A ili B lista:  A, A, a ne A ekvivalent: A  B, A  B, A  B ili “ili”: A  B, A xor B

Metoda zamjene promijenjenih vrijednosti x2) \/ ¬(x3 ≡ x4)) = 1 ((x3 ≡ x4) \/ (x5 ≡ x6)) /\ (¬(x3 ≡ x4) \/ ¬(x5) ≡ x6)) = 1 ( (x5 ≡ x6) ) \/ (x7 ≡ x8)) /\ (¬(x5 ≡ x7) \/ ¬(x7 ≡ x8)) = 1 ((x7 ≡ x8) \ / (x9 ≡ x10)) /\ (¬(x7 ≡ x8) \/ ¬(x9 ≡ x10)) = 1 datom sistemu jednakosti. Kako potvrditi da je potrebno navesti broj takvih setova (demo verzija 2012)

Rješenje Krok 1. Jednostavno rečeno, nakon promjene promjene t1 = x1  x2 t2 = x3  x4 t3 = x5  x6 t4 = x7  x8 t5 = x9  x10 Oprost: (t1 \/ t1) /\ ¬ t2 1 (t2 \/ t3) /\ (¬t2 \/ ¬ t3) =1 (t3 \/ t4) /\ (¬t3 \/ ¬ t4) =1 (t4 \/ t5) /\ (¬t4 \/ ¬ t5) \u003d 1 Pogledajmo jedno jednako: (t1 \/ t2) /\ (¬t1 \/ ¬ t2) \u003d1 XOR preko konjunkcije i disjunkcije: (t1 \/ t2) /\ (¬t1 \/ ¬ t2) = t1  t2 = ¬(t1 ≡ t2) =1 ¬(t1 ≡ t2) =1 ¬( t2 ≡ t3) =1 ¬(t3 ≡ t4) =1 ¬(t4 ≡ t5) =1

Krok2. Analiza sistema do. tk = x2k-1 ? 0) , i tk =1 opklada (0,0) i (1,1).

Krok3. Pidrahunok broja ruža. Skin t može biti 2 odluke, broj t - 5. Uklj. za promjenu t ísnuê 25 = 32 rješenja. Ale skin t vídpovídaê par rješenje x, tobto. izlazni sistem može biti 2 * 32 = 64 rješenja. ID: 64

Način uključivanja dijela ruža jezika )∧(x4→ x5) =1; (y1→y2)∧(y2→y3)∧(y3→y4) ∧(y4→y5) =1; y5→ x5 =1. Nije potrebno oživljavati sve različite skupove x1, x2, ..., x5, y 1, y2, ..., y5 za vidpovídí, kod kojih se pobjedama daje sistem jednakosti. U pravilu je potrebno navesti broj takvih setova.

Rješenje. Krok 1. Posljednja odluka je jednaka x1 1 0 x2 1 0 1 x3 1 0 1 1 x4 1 0 1 1 1 x5 1 0 1 1 1 1 Prvo izjednačavanje - spoj niza operacija, implikacije, završetak 1, zatim. koža sa implikacijama je istina. Implikacija chibne je samo u jednom smjeru, ako je 1  0, u svim ostalim smjerovima (0  0, 0  1, 1  1) operacija se rotira 1. Zapisujemo sljedeću tabelu:

Krok 1. Posledice Uzeto je 6 setova rješenja za x1, x2, x3, x4, x5: (00000), (00001), (00011), (00111), (01111), (11111). Rozmírkovoyuchi na sličan način, dolazimo do vysnovku, shcho za y1, y2, y3, y4, y5 i isti skup rješenja. Jer ravnopravni i nezavisni, tobto. nemaju značajnih promjena, tada će rozvyazannym tsíêí̈ sistemi jednakih (bez poboljšanja trećeg jednakog) biti 6 * 6 \u003d 36 parova "iksív" i "ígrekív". Treća jednaka utakmica: y5→ x5 =1 Opklada na odluku: 0 0 0 1 1 1 Neusklađena opklada: 1 0

Moguće je jednako izostaviti rješenje. Tamo, de y5 = 1, ne odgovara x5 = 0. Takvih parova ima 5. Broj veza u sistemu: 36-5= 31 Odgovor: 31 Treba nam kombinatorika!!!

Metoda dinamičkog programiranja Nije potrebno otkupljivati sve različite skupove vrijednosti za promjene, sa bilo kojim vikonanom je jednak. Kako trebate naznačiti broj takvih setova.

Rješenje Krok1. Analiza uma Livoruha na jednako uzastopno evidentirane operacije, implikacije, prioritet međutim. Prepišite: ((((X 1 → X 2) → X 3) → X 4) → X 5) → X 6 = 1 NB! Koža je napadnuta promjenom da pada ne sprijeda, već sprijeda implikacije!

Krok2. Otkrivanje regularnosti Pogledajmo prvu implikaciju, X 1 → X 2. Tabela istinitosti: X 1 X 2 X 1 → X 2 0 0 1 0 1 1 1 0 0 1 1 1 1. Postoji samo jedna 0 i tri 1, što je rezultat prve operacije.

Krok2. Otkrivena pravilnost Povezujući se sa rezultatom prve operacije x 3 uzimamo: F(x 1 ,x 2) x 3 F(x 1 ,x 2)  x 3 0 0 1 0 1 1 1 0 0 1 1 1 1 0 0 1 1 1 1 0 0 1 1 1 Z dva 0 – dva 1, kožni 1 (í̈h 3) jedan po jedan 0 i 1 (3+3)

Krok 3. Visnovok formula Dakle. možete dodati formule za izračunavanje broja nula N i broj jedinica E i za izjednačavanje i promjena: ,

Krok 4. Popunjavanje tabela Popunjavanje tabele desno za i = 6, računajući broj nula i jedinica nakon pokazivačkih formula; tabela pokazuje kako će se napredovati korak iza fronta: broj promjena 1 2 3 4 5 6 Broj nula N i 1 1 3 5 11 21 Broj jedinica E i 1 2*1+1= 3 2*1 +3= 5 11 21 43 Odgovor: 43

Metoda sa više pitanja postavljanja logičkih varijabli Skala različitih rješenja može biti jednaka ((J → K) → (M N  L))  ((M  N  L) → (¬ J  K))  (M → J ) = 1 de J, K, L, M, N - logičke promjene? Nije potrebno reparirati sve različite skupove vrijednosti J, K, L, M i N u različitim slučajevima, ako ih ima, potrebna je jednakost. Podsjećamo, potrebno je odrediti broj takvih setova.

Rješenje Poštujemo da je J → K = ¬ J  K Zamijenimo promjene: J → K = A, M  N  L =V J)=1 4. (A  B)  (M → J)= 1 5 Očigledno je da A  B za istu vrijednost A i B 6. Pogledajmo preostalu implikaciju M → J =1 J=0 M=0, J=1 M=J=1

Rješenje A  B , U M=J=0 uzimamo 1 + K=0. Ne postoji rješenje. Sa M = 0, J = 1, 0 + K = 0, K = 0 i N í L - bilo da je to, 4 rješenja: ¬ J  K = M N N  LKNL 0 0 0 0 0 1 0 1 0 0 1 jedno

Rješenje 10. Sa M=J=1, 0+K=1 *N * L ili K=N*L potrebno je 4 rješenja: 11. Zajedno može 4+4=8 rješenje Vrijednost: 8 KNL 0 0 0 0 0 1 0 1 0 1 1 1

Džerela informacije: O.B. Bogomolova, D.Yu. Usenkov. B15: novi zadaci i nova rješenja // Informatika, br. 6, 2012, str. 35 - 39. K.Yu. Poliakiv. Logičko usklađivanje // Informatika, br. 14, 2011, str. 30-35. http://ege-go.ru/zadania/grb/b15/, [Elektronski izvor]. http://kpolyakov.narod.ru/school/ege.htm, [Elektronski izvor].

Niní zrostayut vomogi podvishchennya yakostí navchannya shkolyarív. Jedna od najvažnijih inovacija u oblasti matematičkog obrazovanja je uključivanje matematičkih logičkih elemenata u školske programe. Pametno je kotrljati se, kao što logičko znanje igra ludo iluminirajući pripravnik današnjih ljudi.
Nastava elemenata matematičke logike u potpunosti je razvijena u 5–6 razredu, au 7 razredu - uporednik u sistemu rada kod asistenta koji izvodi rad. Potreban sat se može saznati za račun izučavanja ishrane, ako se ne unese jezički minimum osnovne škole (korijen koraka p, korak sa indikatorom šuta, metoda intervala, trigonometrijski gradivo u toku učenja algebre), ali izostavljaju i u praksi robotske čitače.
Ali većinu vremena ovi podaci su podijeljeni na manje od izbornih predmeta.

Tema:"Sistemi logičkih jednakosti" (10. razred)

Ciljevi lekcije:

poznavanje učenika uz razumijevanje sistema logičkih jednakosti; razvoj različitih metoda njihovog usavršavanja, ponavljanje metoda usavršavanja algebarskih sistema i skalarno kreiranje vektora;
razvoj matematičkog mišljenja i logičkog mišljenja učenja, otkrivanja, analiziranja, učvršćivanja znanja u nepoznatoj situaciji;
vihovannya interes za predmet, marljivost, poštovanje.

vlasništvo: shkílna doshka, kreyda, zoshiti, olovke, olívtsí, mreže za izradu sistema od tryoma i chotirma nevídomimi.

HID LESSON

I. Organizacioni momenat

II. Informisani tim lekcijama

Imenuj zapis one u zoshitu.

- Poslednji naporan dan igrali smo logične operacije. Danas nastavljamo sa učenjem logičke ekvivalencije, učeći da razbijamo sistem takve ekvivalencije. Osim toga, treba napomenuti da sistemi logičkih jednakih krše tri puta inače, niži algebarski. Tačnije, na druge načine.

III. Aktuelizacija znanja

– Šta znači uništiti sistem sa dve zamene?
Promeniti sistem sa dve promene - tse znači znati sve opklade (x, y), kako zadovoljiti kožu od zadataka jednakih, ili ga doneti, nema rešenja.
Kako znate kako poboljšati sisteme?

način ugradnje,
način da dodam,
način uvođenja novih promjena,
grafička metoda.

1. Promijeniti sistem izjednačavanja u redovima.

Prvi red - način dodavanja;
Drugi je na grafički način;
Treći je način ugradnje.

a) Klađenje pojam po pojmu jednako, možda: 2 X + 10X = 15 + 9;

12X = 24; X\u003d 2, zamjenjujući vrijednost drugom jednakom, uzimamo: 10 . 2 – 11at= 9, zvjezdice at = 1.

prijedlog:(2;1).

b) Od prvog jednakog, od drugog jednakog,

A (2; 1) - linija linija grafika rijeka.

(2;1) - rješenje sistema.

c) Od prvog jednako do sljedećeg

11at = 15 – 4, 11at = 11, at = 1.

prijedlog: (2;1).

– Šta se naziva skalarno stvaranje vektora?
Skalarno kreiranje vektora je broj koji dozvoljava sabiranje dva vektora kosinusom reza između njih.
Kako napisati skalarnu TV u koordinatnom obliku?

IV. Glavna pozornica

Iskoristivši dvije operacije "disjunkcija" i "konjukcija", pogledajmo Boolean sistem dva jednaka sa dva nevidljiva:

Značaj promjene u jednoj je jednak sa jednom logičnom operacijom za proizvodnju do velikog broja odluka. Yakby rješenje sistema je izraženo deako formula za pevanje, onda smo u slučaju privremenog objavljivanja podataka (koeficijenata izjednačavanja) oduzeli cijelu odluku. Na jednostavnom primjeru imamo bogato značenje rješenja, dakle rješenja sistema zloglasnog izgleda mogu se izraziti formulama naljepnica, ali izgleda da takve formule nemaju takve formule. Nijedna od ovih formula nije pronađena, tako da se sistemi logičkih jednakih razbijaju sopstvenim metodama, iz kojih sada možemo znati starost.
Depozitni sistem sa šest parametara a,b,c,d,m,n, Skin ovih ima dvije vrijednosti 0 ili 1. Također, ukupno je 26 = 64 ups.
Analitički rezultat se može oduzeti logičkim poređenjem i sortiranjem svih 64 tačke.

Zadatak 1.(jedan učenik radi na tabli).

Virishiti sistem, kao a = 0, b = 0, c = 0, d = 0, m = 0, n = 0.

prijedlog: sistem ima 4 rješenja: (1; 1), (0; 1), (1; 0), (0; 0).

Zadatak 2.(Nezavisno u zoshitu uz daljnju ponovnu provjeru).

Virishiti sistem, kao a = 1, b = 0, c = 0, d = 0, m = 0, n = 0.

prijedlog: sistem može imati 2 rješenja: (0; 0), (0; 1).

Slično, moguće je riješiti 62 sistema, prikazujući promjenu parametara a,b,c,d,m,n važeće vrijednosti 0 i 1.
Moguće je kombinovati djela u razredu, tako da možete vidjeti za djela, ako sistem ima jedno rješenje, rješenje je više od rješenja.
At školski kurs matematičari se mogu nazvati više od krugova oko zavdana, yakí može biti virišnost sa dodatnim sistemima logičkih jednakosti.

Zadatak 3.Šest prozirnih tikvica s vodom raspoređeno je u dva paralelna reda po tri tikvice u koži. Na malim prikazima pogled sprijeda i pogled s desne strane. Kroz otvore na zidovima tikvica vidi se čak i voda u kožnoj tikvici iu svim tikvicama koje stoje iza njih. Vznachte, boca za vodu se sipa iz boce kože.

Na malom se vidi da su tikvice pune ili prazne. Mnogo tikvica, koje se mogu koristiti za označavanje šest mjeseci, uspostavlja abecedu koja se sastoji od dva elementa.
Znatno prazna boca - 0, a prazna - 1. Ako je boca prazna, onda se zbrajaju 0 i 1. = (0,1).
Projekcije malenog numeriramo brojevima poput 1 do 5.
Na taj način numeriramo redove tikvica i označimo elemente koji se mogu smjestiti u te redove

Prva projekcija pokazuje da na vrhu nema drugih tikvica, tj. X 11 = 0, X 21 = 0.

Iz pete projekcije je jasno da X 23 = 0, X 22 = 0. Ostale elemente je lako izračunati: X 12 = 1, X 13 = 1.

Analitički postavljajući zadatak da dovede do razvoja sistema izjednačavanja

Može li se sistem izjednačiti, za bilo koju operaciju “+” - disjunkcija, “ . ” – veznik.
Sa drugog nivoa sistema i referentnih tabela konjunkcija i disjunkcija, neophodno je X 21 + X 22 + X 23 = 0 => X 21 = X 22 = X 23 = 0.
Od trećeg jednako => X 11 = 0.
Pretpostavimo da znamo značenja nepoznatog u četvrtom i petom jednakosti sistema:

Svi potrebni i nepoznati članovi prihvataju vrijednosti 0 ili 1, a jednaki se zadovoljavaju logičkim operacijama, tj. uzeti sistem logičkih jednakih.
Kasnije se kao zadatak daju dvije vrste boca, lako je prelomiti put razvoja sistema logičkih jednakosti. Tse vam omogućava da odvojite sat vremena, dajte kraći i jednostavniji način za negovanje.
Pogledajmo metodu transparentnih tablica (metoda mreža) - analognu grafičkoj metodi za rješavanje algebarskih sistema, koja vam omogućava da brzo promijenite sistem jednakosti, da osvetite tri više od nekih promjena.
Ova metoda se zasniva na skalarnom kreiranju vektora.

Yak virishuvati deyakí zavdannya rozdílív A ta B íspitu z íformatika

Lekcija broj 3. logika. Logičke funkcije. Rozvyazannya rivnyan

Veliki broj šefova EDI-ja posvećen je logici jezika. Radi savršenstva, dovoljno je poznavati osnovne zakone logike, poznavanje tablica istinitosti logičkih funkcija jedne i druge dvije. Uvest ću osnovne zakone logike vislovluvana.

Komutativnost disjunkcije i konjunkcije:
a ˅ b ≡ b ˅ a
a^b≡b^a
Distributivni zakon za disjunkciju i konjunkciju:
a ˅ (b^c) ≡ (a ˅ b) ^(a ˅ c)
a ^ (b ˅ c) ≡ (a ^ b) ˅ (a ^ c)
Prečka:
¬(¬a) ≡ a
Nepovršnost:
a ^ ¬a ≡ netačno
Isključi treće:
a ˅ ¬a ≡ tačno
advokat de Morgan:
¬(a ˅ b) ≡ ¬a ˄ ¬b
¬(a ˄ b) ≡ ¬a ˅ ¬b
Oproštaj:
a ˄ a ≡ a
a ˅ a ≡ a
a ˄ istina ≡ a
a ˄ false ≡ false
Poglinannya:
a ˄ (a ˅ b) ≡ a
a ˅ (a ˄ b) ≡ a
Promjena implikacije
a → b ≡ ¬a ˅ b
Promjena identiteta
a ≡ b ≡(a ˄ b) ˅ (¬a ˄ ¬b)

Podnošenje logičkih funkcija

Da li se logička funkcija sa n mijenja - F(x 1 , x 2 , ... x n) može biti umetnuta u tablicu istinitosti. Takva tabela sadrži 2 n skupova izmjena, za koje je za kožu postavljena vrijednost funkcije ovog skupa. Takva metoda je dobra ako je broj promjena mali. Čak i sa n > 5, manifestacija postaje gadno dostupna za inspekciju.

Drugi način je da postavite funkciju sa određenom formulom, dovoljno vikornom jednostavne funkcije. Sistem funkcija (f 1 , f 2 , ... f k ) se ponovo poziva, kao da je logička funkcija, može se izraziti formulom koja eliminiše funkciju f i .

Opet, sistem funkcija (¬, ˄, ˅). Zakon 9 i 10 sa kundacima, koji pokazuju kako se implikacija te istosti manifestuje kroz tranziciju, konjunkciju i disjunkciju.

U stvari, to je novi sistem sa dvije funkcije - preklapanje i konjugacija ili preklapanje i disjunkcija. Iz de Morganovih zakona, postoje izjave koje vam omogućavaju da vidite konjunkciju kroz listing i disjunkciju i da jasno pokažete dis'junkciju kroz listing i konjunkciju:

(a ˅ b) ≡ ¬(¬a ˄ ¬b)
(a ˄ b) ≡ ¬(¬a ˅ ¬b)

Paradoksalno, to je novi sistem koji se sastoji od samo jedne funkcije. Uspostaviti dvije binarne funkcije - antikonjunkciju i antidijunkciju, naslov Pirsove strelice i Šeferov potez koji predstavlja prazan sistem.

Prije skladišta osnovnih funkcija programskog jezika, uključuje zvuk istosti, listing, konjunkciju i disjunkciju. At zadaci EDI-ja redoslijed ovih funkcija je često implikacija.

Pogledajmo neke jednostavne zadatke koji imaju logičke funkcije.

Kancelarija 15:

Dat je fragment tabele istine. Kako jedna od tri funkcije indukcije može pokazati koji fragment?

x1	x2	x3	x4	F
1	1	0	0	1
0	1	1	1	1
1	0	0	1	0

(X 1 → X 2) ˄ ¬ X 3 ˅ X 4
(¬ X 1 ˄ X 2) ˅ (¬ X 3 ˄ X 4)
¬ X 1 ˅ X 2 ˅ (X 3 ˄ X 4)

Funkcija broj 3.

Da biste izvršili zadatak, potrebno je poznavati tablice istinitosti osnovnih funkcija i zapamtiti prioritete operacija. Pretpostavljam da konjunkcija (logičko množenje) ima najveći prioritet i pobjeđuje ranije, nižu disjunkciju (logičko sabiranje). Prilikom izračunavanja nije važno napomenuti da funkcije brojeva 1 i 2 na trećem skupu mogu imati vrijednost 1 i već iz razloga što se fragment ne prikazuje.

Zavdannya 16:

Yakeovi pokazivački brojevi zadovoljavaju um:

(brojevi koji počinju od najvišeg reda, idu po opadajućem) → (broj - momak) ˄ (najmlađi broj - par) ˄ (najveći broj - neuparen)

Kao takvi brojevi, recite više.

13579
97531
24678
15386

Umov je zadovoljan brojem pod brojem 4.

Prva dva broja uma nisu zadovoljna ovim razlozima, jer je mlada figura nesparena. Konjunktura umova je hibnoy, kao jedan od članova konjukture zaloga. Za treći broj, najviša cifra se ne računa. Za četvrti broj razmislite o tome šta se nalazi iznad najmlađe i najstarije cifre broja. Prvi član veznika je takođe tačan;

Zadatak 17: Dvije potvrde davale su sljedeće indikacije:

Prva napomena: Ako je A vino, onda je B tamno vino, a C je nevin.

Još jedna napomena: Winnie dva. I kao da je jedan od tihih kriv i kriv, ko je uskraćen, ali za sebe ne mogu reći.

Koju vrstu vysnovki o vinu A, B i C možete koristiti na postolju da pokažete certifikate?

Vidpovid: Z dokaz dokaza je jasan da su A i B vino, a C je nevin.

Rješenje: Očigledno je moguće dati, uzemljenje na zdravo oko. Ali hajde da pogledamo kako to možete učiniti strogo formalno.

Prva stvar koju treba učiniti je formalizirati govor. Uvodimo tri logičke promjene - A, B i C, čija skin vrijednost može biti tačna (1), što je osnova sumnje na krivicu. Ove indikacije prvog sertifikata date su formulom:

A → (B ˄ ¬C)

Certifikat drugog certifikata daje se formulom:

A ˄ ((B ˄ ¬C) ˅ (¬B ˄ C))

Indikacije oba iskaza smatraju se istinitim i konjunktivnim u odnosu na odgovarajuće formule.

Pogledajmo tabelu istinitosti za ove indikacije:

A	B	C	F1	F2	Ž 1 Ž 2
0	0	0	1	0	0
0	0	1	1	0	0
0	1	0	1	0	0
0	1	1	1	0	0
1	0	0	0	0	0
1	0	1	0	1	0
1	1	0	1	1	1
1	1	1	0	0	0

Sumirani dokazi istine samo u jednom slučaju, što dovodi do nedvosmislenih dokaza - A i B vino, a C - nevin.

Iz analize tabele takođe je jasno da je naznaka drugog sertifikata informativnija. Uz istinitost ove demonstracije, postoje samo dvije moguće opcije- A i B vino, i C - nevino, ili A i C vino, i B - nevino. Prvi certifikat je manje informativan - postoji 5 različitih opcija, ovisno o indikacijama. U potpunosti pokazuje oba svjedoka da daju nedvosmislen iskaz o krivici osumnjičenih.

Logička ekvivalencija i sistemska ekvivalencija

Ajde F(x 1 , x 2 , … x n) je logička funkcija u obliku promjena. Logički jednako može izgledati:

F (x 1, x 2, ... x n) \u003d Z,

Konstanta može biti 1 ili 0.

Logički jednako može biti majka 0 do 2 n različitih rješenja. Ako je Z tačan 1, tada su rješenja skupovi naizmjeničnih tablica istinitosti, za koje funkcija F uzima vrijednost true (1). Reshta set ê rješenja jednaka na C, što je jednako nuli. Na to uvijek možete gledati više nego jednako razumno:

F(x 1 , x 2 , … x n) = 1

Istina, neka bude jednako:

F(x 1 , x 2 , … x n) = 0

Na ovaj način možete ići na ekvivalentan nivo:

¬F(x 1 , x 2 , …x n) = 1

Pogledajmo sistem sa k logičkih linija:

F 1 (x 1 x 2 ... x n) \u003d 1

F 2 (x 1 x 2 ... x n) \u003d 1

F k (x 1 x 2 ... x n) = 1

Odluke sistema su skup promjena u kojima su svi jednaki sistemi pobjednici. U smislu logičkih funkcija, odluka sistema logičkih jednakosti treba biti poznata, za koju je tačna logička funkcija F, koja predstavlja konjunkciju eksternih funkcija F:

F = F 1 ˄ F 2 ˄ … F k

Ako je broj promjena mali, na primjer, manji od 5, onda nije bitno indukovati tablicu istinitosti funkcije F, koja vam omogućava da kažete koliko rješenja sistem može i kako postaviti, dati rješenja.

Neki zavdannyah ÊDI shodo znahodzhennya rješenje sistema logičkih jednakosti, broj zmínnyh syagaê znachennya 10. Todi navesti tablicu istine postaje praktično neprepoznatljiv zavdannyam. Za završetak zadatka potreban je još jedan pidhid. Za dovoljan sistem, nema ravnog neslavan način, vídmínnogo víd nabrajanje, scho omogućava viríshuvati takí avdannya

Kod propozicije na íspit, zadatak donošenja odluke trebao bi zvučati kao da je zasnovan na izgledu specifičnosti sistema rivna. Ponavljam, ne postoji način da se nabroje sve opcije za set izmjena, ne postoji zloglasni način za rješavanje problema. Rješenja moraju biti zasnovana na specifičnostima sistema. Najčešće je prednji dio jednostavnijeg sistema crtati jednak, vikoristički prema zakonima logike. Druga najbolja metoda rozv'yazannya tsgogo zavdannya polagaê u ofanzivi. Trebamo imati kompletne skupove, samo one, za koje funkcija F može imati vrijednost 1. Zamjena za nove tablice istine će biti analogna binarnom stablu odlučivanja. Kožna igla ovog stabla odgovara jednom rješenju i postavlja brojčanik, za koji funkcija F može imati vrijednost 1. Broj igala u stablu određen je brojem rješenja sistema ekvilizacije.

Šta je takvo binarno stablo rješenja i kako će biti, objasnit ću za nekoliko dana.

Zavdannya 18

Koliko različitih skupova vrijednosti logičkih promjena x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, kako zadovoljiti sistem dva jednaka?

Napomena: Sistem može imati 36 različitih rješenja.

Rješenje: Sistem poravnanja uključuje dva poravnanja. Znamo broj odluka za prvi nivo, koje treba deponovati sa 5 zamena - x 1 x 2 ... x 5. Prvo, možete pogledati sistem za 5 rubalja. Kao što je prikazano, sistem ekvilizacije zapravo predstavlja konjunkciju logičkih funkcija. Upravo taj preokret čvrstoće - spoj umova može se posmatrati kao sistem jednakih.

Napravimo stablo rješenja za implikaciju (x1→x2) — prvi član konjunkcije, koji može biti prvi jednak. Os izgleda kao grafička slika drveta:

Stablo se sastoji od dva rivniv za broj zmínnih rivnyan. Prvi ríven označava prvu promjenu X 1 . Dvije igle istog nivoa pokazuju moguće vrijednosti promjene - 1 i 0. Oskílki rivnyannya postavlja implikaciju, tada glava, na yakíy X1 može imati vrijednost 1, imajte na umu da je na tsíy galuzí X2 vrijednost mala 1. Glava, na yak_y X1 vrijednost je 0, ona će generirati dva nula zabude tri vrijednosti X2, rívnimi rješenje, za koje implikacija X 1 → X 2 uzima vrijednost 1. Na koži natpisa, broj promjena se mijenja, što daje rješenje jednako.

setovi qi osi: ((1, 1), (0, 1), (0, 0))

Prodovzhimo pobudov stablo rozv'yazkív, doyuchi napreduje jednako, napreduje implikacija X 2 → X 3 . Specifičnosti našeg sistema su jednake činjenici da je skin nova jednaka vikorist sistemu, jedna promena linije fronta, dodata jedna nova promena. Krhotine promjene X 2 već imaju vrijednost na stablu, zatim na svim stablima, de promjena X 2 može promijeniti vrijednost 1, promjena X 3 također istu vrijednost 1. Jedna igla, de change X 2 može imati vrijednost 0, dati split na dvije igle, de change X 3 uzeti vrijednost 0 i 1. Na ovaj način, dodavanjem novog nivoa kože, vrakhovyuchi yogo specifičnosti, dodajte jedno rješenje . Prvi dan vikenda:

(x1→x2) /\ (x2→x3) /\ (x3→x4) /\ (x4→x5) = 1
Odluka od 6. maja. Os je kao da gledate izvan rješenja stabla za ovo poravnanje:

Još jedna sličnost našeg sistema je slična prvom:

(y1→y2) /\ (y2→y3) /\ (y3→y4) /\ (y4→y5) = 1

Razlika je manja za one koji imaju promjenu Y. Mala kožna rješenja za promjenu X i mogu se kombinirati sa kožnim rješenjima za promjenu Y j, tada je ukupan broj rješenja dobar 36.

Poštovanje, stablo odluka je dato kao broj odluka (po broju grla), a sama odluka zapisana na koži drveta.

Zavdannya 19

Koliko različitih skupova vrijednosti logičkih promjena x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, kako možete zadovoljiti sve liste ispod?

(x1→x2) /\ (x2→x3) /\ (x3→x4) /\ (x4→x5) = 1
(y1→y2) /\ (y2→y3) /\ (y3→y4) /\ (y4→y5) = 1
(x1→ y1) = 1

Ovaj zadatak je modifikacija prednjeg zadatka. Razlika je u tome što je dat još jedan jednak, koji naziva promjene X i Y.

Z jednako X 1 → Y 1 je očigledno, ako X 1 može biti vrijednost 1 (koristi se isto rješenje), onda í Y 1 može biti vrijednost 1. Ovim redoslijedom postoji jedan brojčanik, za koji je X 1 i Y 1 može biti vrijednost 1. X 1 , jednako 0, Y 1 može biti vrijednost, kao 0, dakle í 1. Taj skup kože s X 1, jednak 0, a takvim skupovima u 5 je dato svih 6 skupova u zminny Y. Također, broj rješenja je dobar 31 .

Zavdannya 20

(¬X 1 ˅ X 2) ˄ (¬X 2 ˅ X 3) ˄ (¬X 3 ˅ X 4) ˄ (¬X 4 ˅ X 5) ˄ (¬X 5 ˅ X 1) = 1

Rješenje: Zagonetke o glavnim ekvivalentnostima, hajde da zapišemo našu ekvivalenciju na vidiku:

(X 1 → X 2) ˄ (X 2 → X 3) ˄ (X 3 → X 4) ˄ (X 4 → X 5) ˄ (X 5 → X 1) = 1

Ciklični jezik implikacija znači istovjetnost promjena, tako da je naš jednak ekvivalent jednak:

X 1 ≡ X 2 ≡ X 3 ≡ X 4 ≡ X 5 = 1

Cijena je jednaka dva rješenja, ako su svi X i jednaki ili 1 ili 0.

Zavdannya 21

(X 1 → X 2) ˄ (X 2 → X 3) ˄ (X 3 → X 4) ˄ (X 4 → X 2) ˄ (X 4 → X 5) = 1

Rješenje: Baš kao u problemu 20, u smislu cikličkih implikacija, prijeđimo na istovjetnost, prepisujući jednakost vizualnog:

(X 1 → X 2) ˄ (X 2 ≡ X 3 ≡ X 4) ˄ (X 4 → X 5) = 1

Napravit ćemo stablo odluka za ovo poravnanje:

Zavdannya 22

Koliko rozv'yazkiva može doći u sistem jednakih?

((X 1 ≡X 2) ˄ (X 3 ≡X 4)) ˅(¬(X 1 ≡X 2) ˄ ¬(X 3 ≡X4)) = 0

((X 3 ≡X 4) ˄ (X5 ≡X 6)) ˅(¬(X 3 ≡X 4) ˄ ¬(X5 ≡X 6)) = 0

((X5 ≡X 6) ˄ (X 7 ≡X 8)) ˅(¬(X5 ≡X 6) ˄ ¬(X 7 ≡X8)) = 0

((X 7 ≡X 8) ˄ (X9 ≡X 10)) ˅(¬(X 7 ≡X 8) ˄ ¬(X9 ≡X10)) = 0

ID: 64

Rješenje: Pređimo sa 10 promjena na 5 promjena, nakon što promjena dođe:

Y 1 = (X 1 ≡ X 2); Y 2 \u003d (X 3 ≡ X 4); Y 3 = (X 5 ≡ X 6); Y 4 \u003d (X 7 ≡ X 8); Y 5 \u003d (X 9 ≡ X 10);

Todi prije nego što se radujem viđenju:

(Y 1 ˄ Y 2) ˅ (¬Y 1 ˄ ¬Y 2) = 0

Rivnyannya se može oprostiti pisanjem joge na prizor:

(Y 1 ≡ Y 2) = 0

Prelazeći na tradicionalni oblik, zapišemo sistem nakon što upitamo gledaoca:

¬(Y 1 ≡ Y 2) = 1

¬(Y 2 ≡ Y 3) = 1

¬(Y 3 ≡ Y 4) = 1

¬(Y 4 ≡ Y 5) = 1

Stablo rješenja za sistem je jednostavno i sastoji se od dva stabla sa vrijednostima promjena koje su nacrtane:

Okreni se vihid zmija X, Zeroisably, koža kože zmija 2 vrijednosti zmije X, tanger zmija y 2 5 puška u zmijama X. Dvil Gilka 2 * 2 5 rishens, tako gol .

Poput bahita, skin manager sistema je jednak vimagaêu njegovog pristupa. Uz divlji prijem ê vikonannya ekvivalentne transformacije oprosta jednake. Spílniy priyom ê i pobudov stabla rješenje. Zastosovuvaniy pidhíd često predviđa tablice istinitosti s tim karakteristikama, da će postojati skupovi mogućih vrijednosti općenito, manje ili više ti, za koje funkcija uzima vrijednost 1 (true). Često u predlaganju zadataka nema potrebe za novim stablom odlučivanja, dok se krhotine u fazi klipa mogu uspostaviti kako bi se uspostavila regularnost pojavljivanja novih glava na skin ofanzivnom nivou, jer se kvari npr. zadatak 18.

Zagalo zavdannya znakhodzhennya rešenje sistema logičkih jednakosti je dobra matematička prava.

Zadatak je vrlo važno ručno dekomisionirati, možete povjeriti dekomisijaciju menadžera računala tako što ćete napisati poseban program za dekomisioniranje nivoa i sistema nivoa.

Nije lako napisati takav program. Takav program može lako stati na put uobičajenim zadacima, jer se oni propagiraju u EDI-ju.

Nije iznenađujuće, ali dizajn rješenja sistema logičkih jednakosti je sklopiv i za računar, a kompjuter može imati svoje granice. Računar se lako može završiti iz zadataka, broj izmjena je 20-30, ali je češće potrebno raditi na zadatku većeg proširenja. Na desnoj strani, funkcija je 2 n, koja postavlja broj skupova, i eksponent, koji brzo raste preko broja n. Podovi su brzi, tako da odličan personalni računar ne naiđe na probleme, poput promena 40. maja.

Moj C# program za rješavanje logičkih linija

Napišite program za reviziju logičkih paralela iz raznih razloga, želeći da budete u mogućnosti da poništite ispravnost logičke varijanse testnih zadataka EDI. Drugi razlog je taj što je takav program čudesni zadatak za programiranje, koji vam omogućava da uspijete, što visi sa zadatkom kategorije C u ED.

Ideja iza programa je jednostavna, zasniva se na ukupnom nabrajanju svih mogućih skupova promjenjivih vrijednosti. Oskílki za dato logičko poravnanje ili sistem jednak je broju promjena n u kući, tada je broj setova 2 n, tako da ga morate riješiti. Vykoristovuyuchi osnovne funkcije C# - ukrštanje, dis'junkcija, konjunkcija i ta istost, nije bitno napisati program, kao da za dati skup izmjena izračunati vrijednosti logičke funkcije, koja će dati logički paritet ili sistemski paritet.

Za takav program potrebno je pozvati ciklus za broj skupova, za taj ciklus za broj skupa formirati sam skup, izračunati vrijednost funkcije za skup, a kako je vrijednost veća od 1, tada skup daje rješenje jednako.

Jedino preklapanje, koje je zbog implementacije programa, vezano je od zadataka oblikovanja za skup broj za skup vrijednosti promjene. Ljepota ovog zadatka leži u činjenici da je dat, važan zadatak, zapravo, da se svede na jednostavan zadatak, koji je već više puta okrivljen. Jasno je, da bi bilo jasno da je vrijednost promjene jednaka broju i, da se jedan dodaje nuli, što predstavlja dvostruki zapis broja i. Od sada je složenije dodijeliti skup vrijednosti promijenjenim brojem skupa dobro poznatom unaprijed postavljenom broju prevedenom u dvostruki sistem.

Os izgleda kao funkcija mog C#, kao da krši naš zadatak:

///

/// program za zajebavanje broja odluka

/// logičko poravnanje (sistemi poravnanja)

///

/// logička funkcija - metoda,

/// čiji potpis postavlja DF delegat

///

/// koliko promjena

/// broj odluka

static int SolveEquations (DF zabava, int n)

bool set = novi bool[n];

int m = (int) Math.Pow(2, n); // broj setova

int p = 0, q = 0, k = 0;

//Rekurzivno traženje broja skupova

za (int i = 0; i< m; i++)

//Formiranje skupa nacrta - set,

//broj koji sam dao binarnim manifestacijama

za (int j = 0; j< n; j++)

k = (int) Math.Pow(2, j);

//Izračunavanje vrijednosti funkcije na skupu

Za razumijevanje programa, spodívayus, dovoljno detaljno objašnjenje ideja programa i komentara u njenim tekstovima. Zaustaviću objašnjenje naslova pointed funkcije. Funkcija SolveEquations ima dva ulazna parametra. Fun parametar definira logičku funkciju, koja procjenjuje poravnanje, koje nije uspjelo ili je sistem jednak. Parametar n određuje broj funkcija koje se mijenjaju fun. Kao rezultat, funkcija SolveEquations rotira broj rješenja logičke funkcije, tako da broj takvih skupova, za koje funkcija uzima vrijednost true.

Za naučnike je logično, ako se trenutna funkcija F(x) ulaznog parametra x promijeni u aritmetički, redni broj. Naš tip vikoristovuetsya deblje konstrukcije. Funkcija SolveEquations je dovedena do funkcija višeg reda - funkcija tipa F(f), za koje parametri mogu biti ne samo jednostavne promjene, već i funkcije.

Klasa funkcija koje se mogu proslijediti kao parametar funkciji SolveEquations postavlja se na sljedeći način:

delegate bool DF(bool vars);

Ova klasa bi trebala sadržavati sve funkcije, kao parametar joj se prosljeđuje skup vrijednosti logičkih promjena, datih nizom vars. Kao rezultat, rotira se vrijednost Boolean tipa, što predstavlja vrijednost funkcije za taj skup.

Nasamkinets će voditi program, u kojem će funkcija SolveEquations pobijediti za implementaciju dekalnih sistema logičkih jednakosti. Funkcija SolveEquations je dio klase ProgramCommon u nastavku:

class ProgramCommon

delegate bool DF(bool vars);

static void Main (args niza)

Console.WriteLine("Funkcija I ima rješenje -" +

SolveEquations(FunAnd, 2));

Console.WriteLine ("Funkcija ima 51 odluku -" +

SolveEquations(Fun51, 5));

Console.WriteLine("Funkcija ima 53 odluke -" +

SolveEquations(Fun53, 10));

static bool FunAnd(bool vars)

return vars && vars;

static bool Fun51(bool vars)

f = f && (!vars ||vars);

static bool Fun53 (bool vars)

f = f && ((vars == vars) || (vars == vars));

f = f && (!((vars == vars) || (vars == vars)));

Os izgleda kao rezultati rješenja programa:

10 zadataka za samostalan rad

Ove tri funkcije su ekvivalentne:
1. (X → Y) ˅ ¬Y
2. ¬(X ˅ ¬Y) ˄ (X → ¬Y)
3. ¬X ˄ Y
Dat je fragment tabele istine:

x1	x2	x3	x4	F
1	0	0	1	1
0	1	1	1	1
1	0	1	0	0

Koja od tri funkcije prikazuje fragment:

(X 1 ˅ ¬X 2) ˄ (X 3 → X 4)
(X 1 → X 3) ˄ X 2 ˅ X 4
X 1 ˄ X 2 ˅ (X 3 → (X 1 ˅ X 4))
Tri osobe ulaze u skladište žirija. Odluke se donose, kao da šef žirija glasa za novi, ako ga podržava samo jedan od članova žirija. S druge strane, rješenje nije hvaljeno. Potražite logičku funkciju koja formalizira proces procjene rješenja.
X pobjeđuje od Y, tako da za par bacanja novčića tri puta dobijete "orla". Odredite logičku funkciju da opišete osvajanje X.
Riječi govora su numerisane, počevši od jedan. Propozicija se poštuje ispravno podnesena, jer slijede sljedeća pravila:
1. Ako se tip u numeraciji riječ završava glasom, onda bi sljedeća riječ, kao da nije na mjestu, trebala početi glasom.
2. Ako riječ nije uparena u numeraciji, završava se glasom, onda sljedeća riječ, takva kakva jeste, treba početi od glasa i završiti se glasom.
  Ono što sledi iz narednih predloga je ispravno nagovešteno:
3. Mama je slatka Maša je slatka.
4. Vođa je glava oka.
5. Istina je dobra, ali sreća je bolja.
Skílki ríshen maê rívnyannya:
(a ˄ ¬ b) ˅ (¬a ˄ b) → (c ˄ d) = 1
Ponovo izračunajte konačno rješenje:
(a → b) → c = 0
Koliko odluka se može donijeti takav sistem je jednako:
X 0 → X 1 ˄ X 1 → X 2 = 1
X 2 → X 3 ˄ X 3 → X 4 = 1
X 5 → X 6 ˄ X 6 → X 7 = 1
X 7 → X 8 ˄ X 8 → X 9 = 1
X 0 → X 5 = 1
Skílki ríshen maê rívnyannya:
((((X 0 → X 1) → X 2) → X 3) → X 4) → X 5 = 1

Datum unapred:

Ekvivalentne funkcije b i c.
Fragment sa funkcijom b.
Neka logična promjena P dobije vrijednost 1, ako šef žirija glasa „za“ pohvalu odluke. Izmjene M 1 i M 2 predstavljaju mišljenje članova žirija. Logička funkcija koja traži pozitivnu odluku može se napisati ovako:
P ˄ (M 1 ˅ M 2)
Neka logička promjena P i dobije vrijednost 1, ako je at i-ti Kidan kovanice vipadaê "orao". Logička funkcija koja postavlja dobitni X može se napisati ovako:
¬((¬P 1 ˄ (¬P 2 ˅ ¬P 3 ˅ ¬P 4)) ˅
(¬P 2 ˄ (¬P 3 ˅ ¬P 4)) ˅
(¬P 3 ˄ ¬P 4))
Prijedlog b.
Usklađivanje ima 3 odluke: (a = 1; b = 1; c = 0); (a = 0; b = 0; c = 0); (a=0; b=1; c=0)

Možete vidjeti različite načine i načine razvoja sistema logičkih poravnanja. Tse zvedennya jedan rivnyannya, podudova tablesí istností i razlaganje.

Menadžer: Odvežite sistem logičkih linija:

Pogledaj u metoda svođenja na jedan nivo . Danska metoda prenosa transformacije logičkih jednakih, na način da su stvarna prava dijela jednaka pravoj vrijednosti (tobto 1). Za koga zaustaviti rad logičkog listinga. Podsjetimo da u jednakim terminima postoje sklopive logičke operacije, zamjenjujući ih osnovnim: "ja", "ABO", "NE". Pristupimo heklanju jedan po jedan, jednak u jedan, jednako jak sistem za dodatnu logičku operaciju "I". Na kraju krajeva, sljedeći korak je ponovno kreiranje otrimanog ekvivalencije na osnovu zakona algebre logike i uzimanje konkretnijeg rješenja sistema.

Rješenje 1: Zastosovuêmo inverziju na oba dela prvog nivoa:

Zamislite implikaciju kroz osnovne operacije "ABO", "NE":

Krhotine lijevog dijela su jednake 1, možete ih kombinirati za dodatnu operaciju "I" u jedan jednak, jednak i jači vanjski sistem:

Izvrnem luk prema De Morganovom zakonu i prepravim rezultat:

Može postojati samo jedno rješenje: A =0, B=0 i C=1.

Sljedeći način - brza tabela istine . Krhotine logičkih vrijednosti mogu imati samo dvije vrijednosti, možete jednostavno proći kroz sve opcije i znati prosjek ti, s kojim pobjeđuje sistem jednakih. Stoga ćemo biti jedna globalna tabela istine za sve jednake sisteme i znamo niz traženih vrijednosti.

Rješenje 2: Sastavljamo tabelu istinitosti sistema:








0	0	1	1	0	1

Napívzhirnim je vidio svađu, na kojoj se misli da je zadatak pobijediti. Dakle, A=0, B=0 i C=1.

Metoda raspadanje . Ideja je da se fiksira značenje jedne od promena (stavi í̈ jednako 0 ili 1) onoj za koju treba da bude jednaka. Zatim kasnije možete popraviti značenje druge promjene.

Rješenje 3: Neka je A = 0, onda:

Od prvog nivoa ćemo uzeti B = 0, a zatim sa drugog - Z = 1. Sistemsko rješenje: A = 0, B = 0 i C = 1.

U ÊDI z íformatici često je potrebno imenovati broj rješenja sistema logičkih jednakosti, a da se ne poznaju sama rješenja, za koja se moraju koristiti iste metode. Glavni način da se sazna broj odluka u sistemu logičkih jednakosti jezamjena. Na poleđini je potrebno maksimalno pojednostaviti kožu na osnovu zakona algebre i logike, a zatim preklopne dijelove jednakih zamijeniti novim i odrediti veličinu rješenja novi sistemi. Dali su mi red da ga zamijenim i donesem niz odluka umjesto nje.

Menadžer: Brojevi rozv'yazkív maê vnyannya (A → B) + (C → D) = 1? De A, B, C, D - logičke promjene.

Rješenje: Hajde da uvedemo nove promene: X = A B í Y = C D . Da popravite nove promjene, zapišite kao: X + Y = 1.

Disjunkcija virne u tri vipadke: (0; 1), (1; 0) i (1; 1), sa X i Y - implikacija, to je tačno u tri vipadke i chibnoy - u jednoj. Na to će razlika (0;1) biti potvrđena sa tri moguća parametra. Vipadok (1; 1) - u slučaju devet mogućih prema parametrima izlaznog poravnanja. Otzhe, od svih mogućih rozv'yazkív tsgogo jednakih 3 + 9 = 15.

Ofanzivna metoda određivanja broja ruža u sistemu logičkih jednakosti - binarno stablo. Pogledajmo ovu metodu sa zadnjicom.

Menadžer: Koliko različitih rješenja može biti jednak logičkom sistemu:

Uveden je sistem izjednačavanja:

(x 1 → x 2 )*(x 2 → x 3 )*…*(x m -1 → x m) = 1.

Pretpostavimo to x 1 - Zaista, čak i od prvog ravnog, to je neophodno x 2 tako istina, od drugog - x 3 =1, i do sada x m= 1. Takođe upisujemo (1; 1; …; 1) z m sama ê rješenja sistema. Hajde sada x 1 \u003d 0, onda je moguće x 2 =0 ili x 2 =1.

Ako x 2 Zaista je prihvaćeno da su i druge promjene tačne, odnosno da je kucanje (0; 1; ...; 1) rješenje sistema. At x 2 =0 x 3 =0 ili x 3 =, i do sada. Nastavljajući na ostale promjene, moguće je da su rješenja jednaka sljedećim skupovima promjena (m +1 rješenje, za skin rješenje, vrijednost promjena je m):

(1; 1; 1; …; 1)

(0; 1; 1; …; 1)

(0; 0; 0; …; 0)

Takav pidhid je dobro ilustrovan uz pomoć binarnog stabla. Broj mogućih rješenja je broj različitih pilića starog drveta. Lako je zapamtiti da vrijedi m+1.

	Drvo	Broj odluka
x 1
x2
x 3
		…

U trenucima poteškoća u kupatilu u ogledalu yah ta budoví derika rješenje može shukati rješenje z pobjede tabela istine, Za jedan - dva jednaka.

Prepišimo sistem jednakih na prvi pogled:

Sastavio sam tabelu istine za jednog jednakog:

x 1	x2	(x 1 → x 2)

Sastavljamo tabelu istinitosti za dva jednaka:

x 1	x2	x 3	x 1 → x 2	x 2 → x 3	(x 1 → x 2) (x 2 → x 3)*

Hajde - logična funkcija među promjenama. Logički jednako može izgledati:

Konstanta može biti 1 ili 0.

Logički jednako može biti majka 0 različitih rješenja. Ako je Z tačan 1, tada su rješenja skupovi naizmjeničnih tablica istinitosti, za koje funkcija F uzima vrijednost true (1). Reshta set ê rješenja jednaka na C, što je jednako nuli. Na to uvijek možete gledati više nego jednako razumno:

Istina, neka bude jednako:

Na ovaj način možete ići na ekvivalentan nivo:

Pogledajmo sistem sa k logičkih linija:

Odluke sistema su skup promjena u kojima su svi jednaki sistemi pobjednici. U smislu logičkih funkcija treba znati odluku sistema logičkih jednadžbi, za koju je tačna logička funkcija F, koja predstavlja konjunkciju eksternih funkcija:

Ako je broj izmjena mali, na primjer, manji od 5, onda nije bitno inducirati tabelu istinitosti za funkciju, koja vam omogućava da kažete koliko rješenja može sistem i kako postaviti, šta dati rješenje.

Neki zavdannyah ÊDI shodo znahodzhennya rješenje sistema logičkih jednakosti, broj zmínnyh syagaê znachennya 10. Todi navesti tablicu istine postaje praktično neprepoznatljiv zavdannyam. Za završetak zadatka potreban je još jedan pidhid. Za dovoljan sistem, ne postoji iskvarena metoda, nema grube sile koja vam omogućava da prekršite takav zadatak.

Kod propozicije na íspit, zadatak donošenja odluke trebao bi zvučati kao da je zasnovan na izgledu specifičnosti sistema rivna. Ponavljam, ne postoji način da se nabroje sve opcije za set izmjena, ne postoji zloglasni način za rješavanje problema. Rješenja moraju biti zasnovana na specifičnostima sistema. Najčešće je prednji dio jednostavnijeg sistema crtati jednak, vikoristički prema zakonima logike. Druga najbolja metoda rozv'yazannya tsgogo zavdannya polagaê u ofanzivi. Trebamo imati kompletne skupove, samo one za koje funkcija može imati vrijednost 1. Zamjena za nove tablice istine bit će analog - binarno stablo odlučivanja. Igla kože ovog stabla odgovara jednoj odluci i postavlja brojčanik na kojem funkcija može imati vrijednost 1. Broj igala u stablu odluke raste sa brojem odluka sistema ekvilizacije.

Šta je takvo binarno stablo rješenja i kako će biti, objasnit ću za nekoliko dana.

Zavdannya 18

Koliko različitih skupova vrijednosti logičkih promjena x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, kako zadovoljiti sistem dva jednaka?

Napomena: Sistem može imati 36 različitih rješenja.

Rješenje: Sistem poravnanja uključuje dva poravnanja. Znamo broj odluka za prvi red, koji bi trebao biti deponovan u 5 puta -. Prvo, možete pogledati sistem za 5 rubalja. Kao što je prikazano, sistem ekvilizacije zapravo predstavlja konjunkciju logičkih funkcija. Upravo taj preokret čvrstoće - spoj umova može biti poput sistema jednakih.

Napravimo stablo rješenja za implikaciju () - prvi član konjunkcije, koji se može vidjeti kao prvi jednak. Os izgleda kao grafička slika drveta

Stablo se sastoji od dva rivniv za broj zmínnih rivnyan. Prvi ríven opisuje prvu promjenu. Dvije igle istog nivoa odražavaju moguću vrijednost promjene - 1 i 0. Oskílki rivnyannya postavlja implikaciju, zatim glava, na kojoj je May vrijednost 1, to znači da je malo vrijednosti u ovom krugu 1. Glava, trenutnog maja, vrijednost je 0, generiše dvije kolone sa vrijednostima , tri jednako, drvo je 0 i 1. Implikacije povećanja vrijednosti 1. Na koži natpisa uzima se vrijednost promjene koja daje savršenstvo.

setovi qi osi: ((1, 1), (0, 1), (0, 0))

Prodovzhimo odluku stabla pobudova, dodajući nadolazećoj jednake, dolazeće implikacije. Specifičnosti našeg sistema su jednake činjenici da je skin nova jednaka vikorist sistemu, jedna promena linije fronta, dodata jedna nova promena. Krhotine su već promijenjene na stablu, zatim na svim stablima, kada je vrijednost 1, vrijednost se također mijenja za 1. Jedna igla, de promena maê znachennya 0, daje razdvajanje na dva gílki, de promena brisanje vrednosti 0 i 1. Na ovaj način, koža se dodaje novi nivo, vrakhovyuchi yogo specifičnosti, dodajte jedno rešenje. Prvi dan vikenda:

Odluka od 6. maja. Os je kao da gledate izvan rješenja stabla za ovo poravnanje:

Još jedna sličnost našeg sistema je slična prvom:

Razlika je manja za one koji imaju promjenu Y. Više kožnih rješenja za promjene može se kombinirati sa kožnim rješenjima za promjene, glavni broj rješenja je skuplji 36.

Poštovanje, stablo odluka je dato kao broj odluka (po broju grla), a sama odluka zapisana na koži drveta.

Zavdannya 19

Koliko različitih skupova vrijednosti logičkih promjena x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, kako možete zadovoljiti sve liste ispod?

Ovaj zadatak je modifikacija prednjeg zadatka. Razlika je u tome što je dat još jedan jednak, koji naziva promjene X i Y.

Iz toga slijedi da ako je vrijednost 1 (jedno takvo rješenje vrijedi), onda je vrijednost 1. Ovim redoslijedom postoji jedan brojčanik na kojem se može izračunati vrijednost 1. pa i 1. Na taj skin postavi s, što je dobro 0, a takvih je 5 skupova, svih 6 skupova se mijenja sa Y. Takođe, broj odluka je dobar 31.

Zavdannya 20

Rješenje: Zagonetke o glavnim ekvivalentnostima, hajde da zapišemo našu ekvivalenciju na vidiku:

Ciklični jezik implikacija znači istovjetnost promjena, tako da je naš jednak ekvivalent jednak:

Postoje dva rješenja, ako su sva jednaka, ili 1 ili 0.

Zavdannya 21

Skílki ríshen maê rívnyannya:

Rješenje: Baš kao u problemu 20, u smislu cikličkih implikacija, prijeđimo na istovjetnost, prepisujući jednakost vizualnog:

Napravit ćemo stablo odluka za ovo poravnanje: