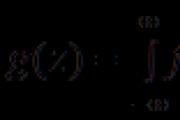Rivnyannya među mrtvima. Opis rješenja

30.07.2020

U ovim temama možemo pogledati mogućnost ponovnog kreiranja funkcije iza njenog gornjeg diferencijala, ali primijeniti redoslijed sa konačnom analizom rješenja.

Buvaê tako, da diferencijalna jednadžba (DC) oblika P (x, y) d x + Q (x, y) d y = 0 može osvetiti u lijevim dijelovima iste diferencijale postojećih funkcija. Tada možemo znati ukupni integral DK, jer unaprijed možemo vidjeti funkciju ukupnog diferencijala.

guza 1

Pogledajmo poravnanje P (x, y) d x + Q (x, y) d y = 0 . Zapis lijevog dijela ima diferencijal trenutne funkcije U(x, y) = 0. Za koji se može vykonuvati Umov ∂ P ∂ y ≡ ∂ Q ∂ x .

Najnoviji diferencijal funkcije U (x, y) = 0 može izgledati d U = ∂ U ∂ x d x + ∂ U ∂ y d y . Molimo shvatite da je ∂ P ∂ y ≡ ∂ Q ∂ x prihvatljivo:

P (x, y) d x + Q (x, y) d y = ∂ U ∂ x d x + ∂ U ∂ y d y

∂ U ∂ x = P (x, y) ∂ U ∂ y = Q (x, y)

Nakon što smo ponovo napravili prvi jednak iz uklonjenog sistema jednakih, možemo uzeti u obzir:

U (x, y) = ∫ P (x, y) d x + φ (y)

Funkciju φ (y) možemo znati iz drugog jednakog sistema:
∂ U (x, y) ∂ y = ∂ ∫ P (x, y) dx ∂ y + φ y "(y) = Q (x, y) ⇒ φ (y) = ∫ Q (x, y) - ∂ ∫ P (x , y) dx ∂ ydy

Dakle, znali smo da će nam trebati funkcija U (x, y) = 0.

guza 2

Nalaz za DC (x 2 - y 2) d x - 2 x y d y = 0 je veliko rješenje.

Rješenje

P (x, y) = x 2 - y 2, Q (x, y) = - 2 x y

Hajde da ponovo razmotrimo kako je um ∂ P ∂ y ≡ ∂ Q ∂ x:

∂ P ∂ y = ∂ (x 2 - y 2) ∂ y = - 2 y ∂ Q ∂ x = ∂ (- 2 x y) ∂ x = - 2 y

Naši umovi su zli.

Na osnovu proračuna možemo odrediti visnovok, koji je lijevi dio vanjske udaljenosti keruvane ê gornji diferencijal djelujuće funkcije U (x , y) = 0 . Trebali bismo znati ovu funkciju.

Vage (x 2 - y 2) d x - 2 x y d y

∂ U ∂ x = x 2 - y 2 ∂ U ∂ y = - 2 x y

Može se integrisati preko x prije poravnanja sistema:

U (x, y) = ∫ (x 2 - y 2) d x + φ (y) \u003d x 3 3 - x y 2 + φ (y)

Sada diferenciranje s obzirom na y oduzimanjem rezultata:

∂ U ∂ y = ∂ x 3 3 - x y 2 + φ (y) ∂ y = - 2 x y + φ y "(y)

Promjenom sistema na drugi nivo možemo pretpostaviti: ∂ U ∂ y = - 2 x y . Tse šta znači
- 2 x y + φ y "(y) = - 2 x y φ y" (y) = 0 ⇒ φ (y) = ∫ 0 d x = C

de S - Postao sam prilično.

Potrebno: U (x, y) \u003d x 3 3 - x y 2 + φ (y) = x 3 3 - x y 2 + C. Integral nadzemnog poravnanja prema van je ê x 3 3 - x y 2 + C = 0.

Pogledajmo još jednu metodu znakhodzhennya funktsíí̈ za vídomim povnym diferencijal. Prenošenje krivolinijskog integrala iz fiksne tačke (x 0 , y 0) u tačku sa promjenjivim koordinatama (x , y):

U (x, y) = ∫ (x 0, y 0) (x, y) P (x, y) d x + Q (x, y) d y + C

Pri različitim vrijednostima integrala, nemoguće je ležati na putu integracije. Možemo to uzeti kao način da integrišemo laman, linije se sortiraju paralelno sa koordinatnim osa.

guza 3

Pronađite globalno rješenje diferencijalne jednadžbe (y - y 2) d x + (x - 2 x y) d y = 0 .

Rješenje

Ponovo provjerimo da je Umova formula ∂ P ∂ y ≡ ∂ Q ∂ x:

∂ P ∂ y = ∂ (y - y 2) ∂ y = 1 - 2 y ∂ Q ∂ x = ∂ (x - 2 x y) ∂ x = 1 - 2 y

Čini se da je lijevi dio diferencijalne jednadžbe predstavljen najvećim diferencijalom trenutne funkcije U(x, y) = 0 . Da bismo znali ovu funkciju, potrebno je izračunati krivolinijski integral tačaka (1 ; 1) prije (x, y). Uzmimo to kao način da integrišemo laman, idemo pravo naprijed y=1 od tačke (1, 1) do (x, 1), a zatim od tačke (x, 1) do (x, y):

∫ (1 , 1) (x , y) y - y 2 dx + (x - 2 xy) dy = = ∫ (1 , 1) (x , 1) (y - y 2) dx + (x - 2 xy) ) dy + + ∫ (x, 1) (x, y) (y - y 2) dx + (x - 2 xy) dy = = ∫ 1 x (1 - 1 2) dx + ∫ 1 y (x - 2 xy) dy = (xy - xy 2) y 1 = = xy - xy 2 - (x 1 - x 1 2) = xy - xy 2

Oduzeli smo ukupno rješenje diferencijalne jednadžbe oblika x y - x y 2 + C = 0.

guza 4

Odaberite globalno rješenje diferencijalne jednadžbe y cos x d x + sin 2 x d y = 0.

Rješenje

Reverzibilno je da je chi potrošni ∂ P ∂ y ≡ ∂ Q ∂ x .

Oskílki ∂ (y · cos x) ∂ y = cos x , ∂ (sin 2 x) ∂ x = 2 sin x · cos x , tada um neće pobijediti. Tse znači da lijevi dio diferencijalne jednadžbe nije ista diferencijalna funkcija. Tse diferencijalno poravnanje sa izmenama koje su podeljene, a za ovu verziju su prikladne druge metode rešavanja.

Kako ste zapamtili pomilovanje u tekstu, budite ljubazni, pogledajte ga i pritisnite Ctrl + Enter

Prikaz problema u perspektivi dva svijeta

Ponovno pronalaženje funkcija broja promjena iza njenog novog diferencijala

9.1. Prikaz problema u pogledu dva svijeta. 72

9.2. Opis rješenja. 72

Ovo je jedan od dodataka krivolinijskom integralu druge vrste.

S obzirom na potpuni diferencijal funkcije dvije promjene:

Upoznajte funkciju.

1. Dakle, kako se ne može svaki um posmatrati kao novi diferencijal funkcije pjevanja U(x,y), tada je potrebno preokrenuti ispravnost postavljanja zadatka, da bi ga obrnuli, potrebno je preispitati potrebu za dovoljnim umom novog diferencijala, kako za funkciju 2-x promjena može izgledati . Tsya umova vyplivaet z tvrdnje o ekvivalentnosti (2) i (3) u teoremi iz prethodnog stava. Čim je imenovan umova vikonan, onda je zadatak bio donijeti odluku, tako da je funkcija U(x,y) može se obnoviti; ako um nije ubijen, onda nema rješenja, pa se funkcija ne može vratiti.

2. Moguće je znati funkciju iza njenog gornjeg diferencijala, na primjer, za dodatni krivolinijski integral II vrste, nakon izračunavanja yogo u pravoj, koja je fiksna tačka ( x 0 ,y 0) ta tačka promjene ( x;y) (Mal. osamnaest):

U ovom rangu je oduzeto da je krivolinijski integral 2. vrste kao potpuni diferencijal dU(x,y) dobra vrijednost funkcije U(x,y) na kraju i kukuruznim tačkama linije integracije.

Znajući sada rezultat, potrebno je osigurati zamjenu dU u krivolinijsku integralnu virazu i izvrši izračunavanje integrala iza lamana ( ACB), vrakhovuyuchi yogo nezavisnost u obliku linija integracije:

na ( AC): na ( SW) :

(1)

U ovom rangu je eliminirana formula za čiju pomoć se koristi funkcija 2. zamjene za njen gornji diferencijal.

3. Moguće je poboljšati funkciju iza njenog gornjeg diferencijala d(U+ const) = dU. Dakle, kao rezultat izvršenja zadatka, uzimaju se u obzir bezlične funkcije, da se jedna vrsta jedne razrađuje na stalnom dodatku.

Primijeniti (ponovno izmišljanje funkcija dvije zamjene za treći diferencijal)

1. Znati U(x,y), kao dU = (x 2 – y 2)dx – 2xydy.

Ponovo potvrđujemo ukupnu razliku uma u funkciji dvije promjene:

Za um novog diferencijala, vikonano, također, funkcija U(x,y) može se obnoviti.

Perevírka: - Tako je.

prijedlog: U(x,y) = x 3 /3 – xy 2 + C.

2. Znati funkciju kao što je

Pregledavamo potrebno i dovoljno znanje o ukupnom diferencijalu funkcija tri promjene: , , kako je dao viraz.

Na rozvyazuvaníy zadatke

svi umovi novog diferencijala viconana, dakle, funkcija se može vratiti (zadatak je ispravno postavljen).

Dodamo funkciju uz pomoć krivolinijskog integrala druge vrste, izračunavši je duž deaky linije, koja je fiksna točka i tačka promjene

(Tsya rivníst vyvoditsya tako sama, kao u dvosvjetskom raspoloženju).

S druge strane, krivolinijski integral II vrste u slučaju totalnog diferencijala ne može ležati u obliku linearne integracije, lakše ga je staviti iza lamana, koji se formira od namotaja, paralelnih sa koordinatom. sjekire. Kada je tačka fiksna, radi jednostavnosti, uzmite tačku sa određenim numeričkim koordinatama, više od toga, tako da tačke i na celoj liniji integracije imaju mentalnu osnovu krivolinijskog integrala (tako da su funkcije, i, prekidne -besplatno). Da biste poboljšali ovo poštovanje za ovaj zadatak, možete uzeti fiksnu tačku, na primjer, tačku M 0. Todi na koži od nogu lamanoi matimemo

10.2. Proračun površinskog integrala prve vrste. 79

10.3. Deyaki programi površinskog integrala prve vrste. 81

Kakav je standardni izgled $P \ lijevo (x, y \ desno) \ cdot dx + Q \ lijevo (x, y \ desno) \ cdot dy = 0 $, u kom slučaju je lijevi dio posljednji diferencijal stvarna funkcija $ F \ lijevo ( x,y\desno)$, naziva se jednakom novi diferencijali.

Jednadžba u najnovijim diferencijalima može se prepisati kao $dF \ lijevo (x, y \ desno) = 0 $, de $ F \ lijevo (x, y \ desno) $ - takva funkcija da $ dF \ lijevo (x, y \desno)=P\levo(x,y\desno)\cdot dx+Q\levo(x,y\desno)\cdot dy$.

$dF\left(x, y\desno) = 0$: $\int dF\left(x, y\right) = F\left(x, y\right)$; integral u nultom desnom dijelu skupljeg prilično konstantnog $C$. Dakle, konačno rješenje ove jednadžbe u implicitnom obliku može izgledati kao $ F \ lijevo (x, y \ desno) = C $.

Da bi ova diferencijalna jednakost bila jednaka u drugim diferencijalima, potrebno je i dovoljno da Umov $\frac(\partial P)(\partial y) =\frac(\partial Q)(\partial x) $. Ako je dodijeljen pametni vikonan, onda postoji takva funkcija $F\left(x,y\right)$, za koju možete napisati: $dF=\frac(\partial F)(\partial x) \cdot dx+ \frac(\partial F)(\partial y) \cdot dy=P\left(x,y\right)\cdot dx+Q\left(x,y\right)\cdot dy$ parcijalni F)(\partial x) = P\left(x,y\right)$ i $\frac(\partial F)(\partial y) = Q\left(x,y\right)$.

Integrabilno prije $\frac(\partial F)(\partial x) =P\left(x,y\right)$ preko $x$ i $F\left(x,y\right)=\int P\ left( x,y\right)\cdot dx +U\left(y\right)$, gdje je $U\left(y\right)$ dovoljna funkcija od $y$.

Uzmimo to ovako, tako da je zadovoljen još jedan spin $\frac(\partial F)(\partial y) = Q\left(x, y\right)$. Za koje možemo razlikovati $F\left(x,y\right)$ u odnosu na $y$ i izjednačiti rezultat sa $Q\left(x,y\right)$. Opciono: $\frac(\partial )(\partial y) \left(\int P\left(x,y\right)\cdot dx \right)+U"\left(y\right)=Q\left( x,y\desno)$.

Dalje rješenje je:

za ostatak jednakosti znamo $U"\left(y\right)$;
integrabilni $U"\left(y\right)$ i poznati $U\left(y\right)$;
zamjenjujući $U\left(y\right)$ za jednakost $F\left(x,y\right)=\int P\left(x,y\right)\cdot dx +U\left(y\right)$ a funkcija $F\left(x,y\right)$ je rezidualno uzeta.

Znamo razliku:

$U"\left(y\right)$ je integrabilan u odnosu na $y$ i $U\left(y\right)=\int \left(-2\right)\cdot dy =-2\cdot y$ poznato je.

Poznati rezultat: $F\left(x, y\desno) = V\left(x, y\desno) + U\left(y\right) = 5\cdot x\cdot y^(2) +3\cdot x\cdot y-2\cdot y$.

Rješenje možemo zapisati na sljedeći način: $F \ lijevo (x, y \ desno) = C $, i samo:

Poznato privatno rješenje $F\left(x,y\right)=F\left(x_(0) ,y_(0) \right)$, gdje je $y_(0) =3$, $x_(0) =2 $:

Privatno rješenje može izgledati ovako: $5 cdot x cdot y ^ (2) +3 cdot x cdot y-2 cdot y = $102.

Imenovanje 8.4. Diferencijal jednak umu

de
nazivaju jednakim drugim diferencijalima.

S poštovanjem, da je lva dio ovoga jednak vrhunskom diferencijalu postojeće funkcije.
.

Na nečuvenom imanju možete platiti porez (8,4) na licu mjesta

Zamjenik jednak (8,5) može se vidjeti jednak

izvođenje takvog integralnog izjednačenja (8.4). Dakle, da bi se riješila jednačina (8.4) potrebno je poznavati funkciju
. Vídpovídno do vzdannya vnyannia (8.4), možda

(8.6)

funkcija
znat ćemo, kao funkcija, kao zadovoljavanje jednog od ovih umova (8.6):

de - prilično funkcija, poput taloženja vode .

Funkcija
biti prikazan na takav način da je izraz drugog uma bio pobjednički (8.6)

(8.7)

Po virazu (8.7) i funkcija je određena
. Slanje í̈í̈ na viraz za
da otrimuyut zagalny íntegra vikhídnogo ívnyannya.

Zadatak 8.3. Integrisati rijeku

Evo
.

Otzhe, tse rívnyannya je dovedena do tipa diferencijalnog rívnyan u najnovijim diferencijalima. funkcija
hajde da se šalimo

sa druge strane,

Na broj vipadkiv umova
ne možeš zeznuti.

Upravo tako, jednak je tipu koji se posmatra, da se pomnoži sa takozvanim integrirajućim multiplikatorom, koji je, u divljem raspoloženju, samo funkcija ili .

Kako jedan jednak ima integrirajući množitelj u koji se može samo položiti , tada se formuli dodjeljuje vin

de staging može biti manje funkcionalan .

Slično, kako integrirati množitelj, kako uplatiti samo nekoliko , Zavisi od formule

de staging
može biti manje funkcionalan .

Vidsutníst u izazivanju spívvídníshnyah, na prvom koraku promjene , a drugi - zminnoyu ê predznak osnove integrirajućeg množitelja za dato izjednačenje.

Zadatak 8.4. Dovedite cijenu jednaku u zadnjim diferencijalima.

Pogledajmo postavku:

Tema 8.2. Linearno diferencijalno poravnanje

Imenovanje 8.5. Diferencijalno poravnanje
naziva se linearnom, kao da je linearna funkcija , í̈í̈ like i nemojte se osvećivati na stvaranju funkcije shukano i í̈í̈ pokhídnoí̈.

Pogled odozgo na linearno diferencijalno poravnanje sličan je sljedećem:

(8.8)

Kako spivvídnoshní (8.8) dio prava
, Uzmi jednako se naziva linearno homogeno. Uzmite vipadku, ako je pravi dio
, Takvo izjednačavanje se naziva linearno heterogeno.

Pokažimo da se jednačina (8.8) može integrirati kvadraturama.

U prvoj fazi možemo pogledati linearnu uniformnost.

Takvo je jednako jednakom promjenama koje su podijeljene. Istinito,

;

Ostatak spívvídnoshnja vznachaê zagalne ríshennya linearne uniforme rívnyannia.

Za traženje divljeg rješenja linearnog, heterogenog poravnanja, koristi se metoda varijacije slične postiynoy. Ideja metode je da rješenje linearnog neujednačenog poravnanja izgleda kao rješenje uniformnog uniformnog poravnanja, proteo je prilično brz biti zamijenjen drugom funkcijom
, koja je svrha imenovanja. Oče, molim te:

(8.9)

Zamjena za spívvídnoshennia (8.8) virazi, vídpovídní
і
, uzeto

Zamjenom preostale viraze u spivvídnenniji (8.9), oni dobijaju globalni integral linearnog nehomogenog poravnanja.

Na ovaj način, glavno rješenje linearne neujednačene trase obilježavaju dvije kvadrature: globalno rješenje linearne ravnomjerne trase i konačno rješenje linearne neujednačene trase.

Zadatak 8.5. Integrirajte rijeku