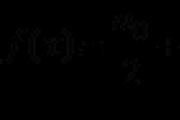নিয়ম এবং পার্থক্যের সূত্রগুলি ভাঁজ ফাংশনের অনুরূপ। ভাঁজ ফাংশন

ফাংশন ভাঁজ চেহারাএটাকে "ফোল্ডেবল ফাংশন" বলে ডাকা ঠিক নয়। উদাহরণস্বরূপ, আরও বেশি মিলিত হচ্ছে, কিন্তু ভাঁজ ফাংশনটি vіdmіnu vіd-এ নয়।

tsіy statti mi এ আমরা s বোঝার বুঝব ভাঁজ ফাংশন, প্রাথমিক ফাংশনের গুদামগুলিতে її দেখাতে শেখার জন্য, আমরা বৈশিষ্ট্যযুক্ত অ্যাপ্লিকেশনগুলির її অনুরূপ এবং রিপোর্টযোগ্য সমাধানের পরিচিতির সূত্র দিই।

নিখুঁত অ্যাপ্লিকেশনের ক্ষেত্রে, আমরা ক্রমাগত অনুরূপগুলির টেবিল এবং পার্থক্যের নিয়মগুলিকে বিজয়ী করি, তাই আপনার চোখের সামনে সেগুলি ছাঁটাই করুন।

ভাঁজ ফাংশন- এটি একটি ফাংশন, যার যুক্তিটিও একটি ফাংশন।

আমাদের মতে, উদ্দেশ্য সবচেয়ে যুক্তিসঙ্গত. চতুরভাবে, আপনি f(g(x)) বোঝাতে পারেন। অর্থাৎ, f(g(x)) ফাংশনের আর্গুমেন্ট হিসাবে g(x)।

উদাহরণস্বরূপ, ধরুন f হল আর্ক ট্যানজেন্টের ফাংশন, এবং g(x) = lnx হল প্রাকৃতিক লগারিদমের ফাংশন, সুতরাং ফোল্ডিং ফাংশন f(g(x)) হল arctg(lnx) এর ফাংশন। আরেকটি বাট: চ চতুর্থ ধাপে লিঙ্ক করার ফাংশন, এবং - tsila যুক্তিসঙ্গত ফাংশন (বিস্ময়), todi .

নিজস্ব উপায়ে, g(x) একটি সংকোচিত ফাংশন হতে পারে। উদাহরণ স্বরূপ, . চতুরভাবে এমন ভিরাজ হিসেবে চেনা যায় . এখানে f সাইনের ফাংশন, বর্গমূলের পরিবর্তনের কাজ, - শটগান যুক্তিসঙ্গত ফাংশন. এটা স্বীকার করা যৌক্তিক যে ফাংশন বিনিয়োগের ধাপ একটি চূড়ান্ত মত হতে পারে স্বাভাবিক সংখ্যা.

প্রায়ই আপনি শুধু একটি ফাংশন কল করতে পারেন ফাংশন রচনা।

পরিচিত ভাঁজ ফাংশনের সূত্র।

বাট

ব্যবহারিক ভাঁজ ফাংশন জানুন.

সমাধান।

যে ক্ষেত্রে f একটি বর্গাকার ফাংশন, এবং g(x) = 2x+1 একটি রৈখিক ফাংশন।

রিপোর্টের অক্ষ হল একটি অনুরূপ ভাঁজ ফাংশনের জন্য বিভিন্ন সূত্র সহ একটি সমাধান:

বাহ্যিক ফাংশনগুলি দেখে আগে থেকে জিজ্ঞাসা করে আমি কী করতে যাচ্ছি তা জেনে নেওয়া যাক।

ওটজে,

bachite মত, ফলাফল zbіgayutsya.

বিপথগামী না হওয়ার চেষ্টা করুন, যেমন একটি ফাংশন є f, কিন্তু g(x) এর মতো।

সম্মানের জন্য একটি বাট দিয়ে এটি ব্যাখ্যা করা যাক।

বাট

ভাঁজ করার ব্যবহারিক কার্যাবলী জানুন।

সমাধান।

প্রথম ক্ষেত্রে, f হল বর্গ ফাংশন, এবং g(x) হল সাইন ফাংশন, তাই
.

অন্য দৃষ্টিতে, f হল সাইনাস ফাংশন এবং a হল স্টেট ফাংশন। পরবর্তীতে, সূত্রের জন্য, অতিরিক্ত ভাঁজ ফাংশন হতে পারে

অনুরূপ ফাংশনের সূত্র দেখা যায়

বাট

একটি ফাংশন পার্থক্য .

সমাধান।

কোন বাট ভাঁজ ফাংশন জন্য, আপনি মানসিকভাবে লিখতে পারেন কিভাবে , de - সাইনের ফাংশন, তৃতীয় ধাপের লিঙ্কের ফাংশন, বেস e-এর লগারিদমের ফাংশন, আর্ক ট্যানজেন্ট নেওয়ার ফাংশন এবং দ্বিতীয় ধাপের রৈখিক ফাংশন।

অনুরূপ ভাঁজ ফাংশনের সূত্রের পিছনে

এখন আমরা জানি

আমরা বিয়োগকৃত মধ্যবর্তী ফলাফল একসাথে নির্বাচন করি:

ভয়ানক কিছু নেই, একটি matrioshka মত ভাঁজ ফাংশন বাছাই।

যার উপর আমি নিবন্ধটি শেষ করতে পারি, ইয়াকবি ঝাডনে আলে...

Bazhano স্পষ্টভাবে বুঝতে, যদি আপনি পার্থক্য নিয়ম এবং অনুরূপ বেশী টেবিল সেট আপ, এবং যদি একটি অনুরূপ ভাঁজ ফাংশন সূত্র.

অনুগ্রহ করে বিশেষভাবে সম্মান করুন। চলুন ফোল্ডিং ফাংশন প্রসঙ্গে ফাংশন প্রবর্তন সম্পর্কে কথা বলা যাক। এছাড়াও, আপনি আপনার শক্তি সঞ্চয় করবেন এবং আপনি যদি ভাগ্যবান হন তবে আপনি সফল হবেন।

আসুন সহজ অ্যাপ্লিকেশন থেকে শিখি। ফাংশন আপনি দেখতে পারেন কিভাবে আমি এটি ভাঁজ করি: g(x) = tgx , . এছাড়াও, আপনি অবিলম্বে সূত্র pokhіdnoї ভাঁজযোগ্য ফাংশন zastosovuvat করতে পারেন

একটি অক্ষ ফাংশন ভাঁজযোগ্য বলা যাবে না।

এই ফাংশনটি তিনটি ফাংশনের সমষ্টি, 3tgx i 1। হোচা - є কোলাপসিবল ফাংশন: - স্ট্যাটিক ফাংশন (চতুর্মুখী প্যারাবোলা), এবং f - স্পর্শক ফাংশন। সেই লক্ষ্যে, আমরা সুমি পার্থক্য সূত্র রাখি:

আমি নিম্নলিখিত ভাঁজ ফাংশন সম্পর্কে আমার জ্ঞান হারিয়েছি:

টম

Spodіvaєmosya, scho আপনি সারাংশ ধরা.

আরও আশ্চর্যজনক হওয়ার জন্য, আপনি নিশ্চিত করতে পারেন যে ভাঁজ ফাংশনগুলি ভাঁজ ফাংশনের গুদামে অন্তর্ভুক্ত করা যেতে পারে এবং ভাঁজ ফাংশনগুলি ভাঁজ ফাংশনের স্টোরেজ অংশ হতে পারে।

ফাংশনের স্টোরেজ অংশগুলির জন্য বাটটি কীভাবে সাজানো হয় .

পারচেএটি একটি কোলাপসিবল ফাংশন, যেমন আপনি কল্পনা করতে পারেন, যেখানে f হল বেস 3 এর লগারিদম ফাংশন, এবং g(x) হল দুটি ফাংশনের সমষ্টি і . Tobto, .

অন্যভাবে, আসুন h (x) ফাংশন নিয়ে কাজ করি। জিতেছে .

দুটি ফাংশনের যোগফল হল , ডি - সাংখ্যিক সহগ 3 সহ ফোল্ডিং ফাংশন। - একটি ঘনক্ষেত্রের সাথে লিঙ্ক করার ফাংশন; - কোসাইন ফাংশন; - রৈখিক ফাংশন।

দুটি ফাংশনের যোগফল i , de - কলাপসিবল ফাংশন, - সূচকীয় ফাংশন, - স্ট্যাটিক ফাংশন।

এই ভাবে,

তৃতীয়, যাওযাক যে পুরো যুক্তিসঙ্গত ফাংশন

স্কোয়ারিংয়ের কাজ, - বেসের লগারিদমের কাজ e.

পিতা, .

প্রস্তাবিত:

p align="justify"> এখন ফাংশনের গঠন বোঝা গেছে এবং এটা স্পষ্ট হয়ে গেছে কিভাবে সূত্র এবং ক্রমানুসারে її পার্থক্যে zastosovuvat।

বিভিন্ন ডিফারেন্সিয়েশন ফাংশনে (ভবিষ্যতের চিহ্ন) আপনি একই ধরনের কাজের ভিন্নতা থেকে শিখতে পারেন।

ফরোয়ার্ড আর্টিলারি প্রস্তুতির পরে, ফাংশনের 3-4-5 সংযুক্তি সহ কম ভীতিকর স্টক থাকবে। এটা সম্ভব, আপনি যদি দুটি বাট ধাপ, তারা ভাঁজ মত হবে, কিন্তু আপনি যদি তাদের বুঝতে (আপনি ভুক্তভোগী কিনা), তারপর ডিফারেনশিয়াল হিসাবের বাকি সবকিছু শিশুসুলভ জ্বর দেওয়া যেতে পারে।

বাট 2

সম্পর্কিত ফাংশন জানুন

যেহেতু এটি উদ্দেশ্য ছিল, প্রয়োজনীয় ভাঁজ ফাংশন সহ, আমরা পরিবর্তন করব, এটি প্রয়োজনীয় অধিকাররোজিব্রতীশ্য সন্নিবেশে। শান্ত পরিস্থিতিতে, যদি আপনি সন্দেহ করেন, আমি সঠিক কৌশলটি অনুমান করব: উদাহরণস্বরূপ, "iks" এর শেষ মানটি নিন এবং "ভয়ংকর ভিরাজ"-এ অর্থ রাখার চেষ্টা করুন (কালো ভাবনা)।

1) আমাদের পিঠে ভিরাজ গুনতে হবে, তারপর, যোগফল সবচেয়ে বড় বিনিয়োগ।

2) তারপর, লগারিদম গণনা করা প্রয়োজন:

4) আসুন ঘনক্ষেত্রে কোসাইন যোগ করি:

5) পঞ্চম সংক্ষিপ্ত মূল্যে:

6) І, nareshti, প্রকৃত ফাংশন নিজেই বর্গমূল:

ভাঁজ ফাংশন পার্থক্য সূত্র zastosovyvaetsya বিপরীত ক্রমে, সবচেয়ে গুরুত্বপূর্ণ ফাংশন আকারে, অভ্যন্তরীণ করতে। আমরা দেখি:

ক্ষমা ছাড়া চেবটো:

1) বর্গমূল দেখুন।

2) খুচরা যত্ন নিন, দুষ্ট নিয়ম

3) Pokhіdna ট্রিপলেট শূন্য থেকে বেশি ব্যয়বহুল। অন্য ডোদানে, আমরা একটি পদক্ষেপ (কিউব) নিই।

4) আসুন কোসাইনটি একবার দেখে নেওয়া যাক।

6) আমি, নরেষ্টি, সবচেয়ে বড় আমানত দেখে নিন।

হতে পারে এটি আরও গুরুত্বপূর্ণ, তবে এটি এখনও সেরা প্রাণী বাট নয়। উদাহরণস্বরূপ, কুজনেটসভের নির্বাচন নিন এবং আপনি নির্বাচিত চেহারার সমস্ত সৌন্দর্য এবং সরলতার প্রশংসা করবেন। আমার মনে আছে যে আমি ঘুমের জন্য একটি জিনিস দিতে চাই, পুনর্বিবেচনা করতে চাই, একজন শিক্ষার্থী কী স্মার্ট, যেমন আপনি ভাঁজ করার ফাংশন জানেন, কী স্মার্ট নয়।

একটি স্বাধীন সমাধানের একটি আপত্তিকর উদাহরণ।

বাট 3

সম্পর্কিত ফাংশন জানুন

ইঙ্গিত: রৈখিকতার নিয়ম এবং সৃষ্টির পার্থক্যের নিয়ম পিছনে পিছনে রয়েছে

বাহ্যিকভাবে, সমাধান হল যে এটি পাঠের অনুরূপ।

আরও কমপ্যাক্ট এবং সুন্দর কিছুতে এগিয়ে যাওয়ার সময় এসেছে।
এটি একটি বিরল পরিস্থিতি নয়, কারণ বাট দুটি নয়, তিনটি ফাংশন দেওয়া হয়েছে। কিভাবে বুঝবেন তিন গুণকের কাজ ভালো হয়?

বাট 4

সম্পর্কিত ফাংশন জানুন

আমরা একটু অবাক হই, কিন্তু কেন তিনটি ফাংশনকে দুটি ফাংশনে রূপান্তর করা যায় না? উদাহরণস্বরূপ, ইয়াকবিতে আমাদের দুটি সমৃদ্ধ আর্টিকুলেশন ছিল, তারপরে খিলানগুলি খোলা সম্ভব ছিল। কিন্তু অ্যাপ্লিকেশানে বিভিন্ন ধরনের সমস্ত ফাংশন: ধাপ, সূচক এবং লগারিদম।

এই ধরনের পরিস্থিতিতে, এটি প্রয়োজনীয় ধারাবাহিকভাবেসৃষ্টির পার্থক্যের নিয়ম বন্ধ কর দুইবার

ফোকাস এই সত্যটির উপর যে "y" এর জন্য আমাদের একটি উল্লেখযোগ্যভাবে আলাদা দুটি ফাংশন রয়েছে: , এবং "ve" এর জন্য - লগারিদম:। কেন আপনি এত বিরক্ত হতে পারেন? একটি হিবা - কেন দুই গুণ এবং নিয়ম কাজ করে না? ভাঁজযোগ্য কিছুই নেই:

এখন হঠাৎ করেই নিয়ম হারিয়ে ফেললেন মাথানত করা:

আপনি এখনও রাগান্বিত হতে পারেন এবং মন্দিরগুলির জন্য নিজেকে দোষ দিতে পারেন, তবে এই পরিস্থিতিতে নিজেকে এমন চেহারায় হারানো ভাল - এটি উল্টে দেওয়া সহজ।

একটি দৃষ্টি নিতম্ব অন্য উপায়ে ভাঙ্গা যেতে পারে:

সমাপ্তির আপত্তিকর উপায় একেবারে সমান।

বাট 5

সম্পর্কিত ফাংশন জানুন

এটি একটি স্বাধীন সমাধানের উদাহরণ, প্রথম স্থানে, প্রথম উপায়ে।

আসুন ভগ্নাংশ সহ সাদৃশ্যপূর্ণ অ্যাপ্লিকেশনগুলি দেখে নেওয়া যাক।

বাট 6

সম্পর্কিত ফাংশন জানুন

এখানে আপনি কয়েকটি উপায়ে যেতে পারেন:

Abo এই মত:

কিন্তু সমাধান হল আরও কম্প্যাক্টলি লেখা, যেমন প্রথম লাইনে, প্রাইভেট ডিফারেন্সিয়েশনের নিয়মকে হারানো। , পুরো নম্বরের জন্য গ্রহণ করা হচ্ছে:

নীতিতে, বাট ভেঙে গেছে, এবং আপনি যদি এমন চেহারায় যোগ থেকে নিজেকে বঞ্চিত করেন তবে আপনাকে ক্ষমা করা হবে না। আলে, স্পষ্ট হওয়ার জন্য, এক ঘন্টার জন্য, এটিকে কালো করে দাও, কিন্তু কেন আপনি এটি বলতে পারেন না?

আসুন সংখ্যাগুলিকে স্লিপিং ব্যানারে নিয়ে আসি এবং শটের ট্রিপল সারফেস পাই:

অতিরিক্ত প্রশ্নের বিয়োগ সত্য যে ক্ষমা পরিচিত সময়ে অনুমতি দেওয়া হবে না, কিন্তু সাধারণ স্কুল রূপান্তর এ. অন্যদিকে, ভিক্লদাচি প্রায়ই কাজটি প্রত্যাখ্যান করে এবং আরও খারাপের "পথে আনতে" বলে।

একটি স্বাধীন দৃষ্টিভঙ্গির জন্য সবচেয়ে সহজ উদাহরণ:

বাট 7

সম্পর্কিত ফাংশন জানুন

আমরা পরিচিতদের পরিচিতি আয়ত্ত করতে থাকি এবং সাথে সাথে আমরা সাধারণ বিচ্যুতির দিকে তাকাতে পারি, যদি "ভয়ানক" লগারিদমটি পার্থক্যের জন্য প্রচার করা হয়

ভিজ্যুয়ালাইজেশনের অপারেশনকে ডিফারেন্সিয়েশন বলা হয়।

সবচেয়ে খারাপের উপাধির সহজতম (এবং সহজ নয়) ফাংশনগুলির মধ্যে পার্থক্য সম্পর্কে সমস্যার বিকাশের ফলস্বরূপ, যুক্তির উন্নতির মধ্যে, পার্থক্যের অনুরূপ এবং সুনির্দিষ্টভাবে সংজ্ঞায়িত নিয়মগুলির একটি টেবিল উপস্থিত হয়েছিল। আইজ্যাক নিউটন (1643-1727) এবং গটফ্রাইড উইলহেম লিবনিজ (1646-1716) অতীতের জ্ঞানের ক্ষেত্রে প্রথম।

অতএব, আমাদের ঘন্টায়, কোন ফাংশন আছে কিনা তা জানার জন্য, ফাংশনের উন্নতি থেকে আর্গুমেন্টের উন্নতির মধ্যে পার্থক্য গণনা করার প্রয়োজন নেই, তবে এটির সাথে অনুরূপগুলির টেবিলের গতি বাড়ানো প্রয়োজন। পার্থক্যের নিয়ম। ভবিষ্যতের জ্ঞানের জন্য, একটি আক্রমণাত্মক অ্যালগরিদম ব্যবহার করা উচিত।

পোখিদনু জানার জন্য, স্ট্রোক চিহ্নের অধীনে ভিরাজ প্রয়োজন গুদাম সহজ ফাংশন প্রসারিত ta vznachiti, yakami (tvir, যোগ, ব্যক্তিগত)এই ফাংশন সম্পর্কিত। Dalі pokhіdnі প্রাথমিক funktsіy znachimo іn the tablesі іn pokhіdnih, এবং সূত্র pokhіdnih creativ, sum ta chasto - іn পার্থক্যের নিয়ম। প্রথম দুটি অ্যাপ্লিকেশনের পরে ডেটা পার্থক্য করার জন্য অনুরূপ নিয়মের সারণী।

উদাহরণ 1.সম্পর্কিত ফাংশন জানুন

সমাধান। পার্থক্যের নিয়ম থেকে, এটা স্পষ্ট যে ফাংশনের যোগফল একই রকম ফাংশনের যোগফলের সমান, অর্থাৎ।

অনুরূপদের টেবিল থেকে, এটা স্পষ্ট যে "ইক্সা" এককটির মতো এবং সাইনটি কোসিনাস। pokhіdnyh এর যোগফলের জন্য qi মানগুলিকে প্রতিস্থাপন করুন এবং আমরা জানি pokhіdnu এর প্রয়োজনীয় মানসিক কাজ:

বাট 2সম্পর্কিত ফাংশন জানুন

সমাধান। ভিন্নভাবে, যেন আমি আমার যোগফল হারাতে যাচ্ছি, একটি ধ্রুবক গুণক সহ অন্য কোনো সংযোজনে, আমি খারাপের চিহ্নের জন্য এটিকে দোষ দিতে পারি:

যতক্ষণ খাবারকে দোষারোপ করা হয়, তারাগুলি নেওয়া হয়, দুর্গন্ধ, একটি নিয়ম হিসাবে, অনুরূপগুলির টেবিলের সাথে পরিচিত হওয়ার পরে এবং পার্থক্যের সহজতম নিয়মগুলি পরিষ্কার হয়ে যায়। তাদের আগে, আমরা একযোগে পাস.

অনুরূপ সহজ ফাংশন টেবিল

1. Pokhіdna ধ্রুবক (সংখ্যা)। একটি সংখ্যা আছে কিনা (1, 2, 5, 200 ...), এই ধরনের একটি ফাংশন ভিন্ন হবে। শূন্য পর্যন্ত রাখুন। এটা মনে রাখা আরো গুরুত্বপূর্ণ, যে আরো প্রায়ই প্রয়োজন হয়
2. Pokhіdna nezalezhnaya zminnoy। বেশিরভাগই "ইক্সা"। একটি সুস্থ একাকীত্ব ভুলে যান. Tse তাই গুরুত্বপূর্ণভাবে এটি একটি দীর্ঘ সময়ের জন্য মনে রাখবেন
3. Pokhіdna ধাপ। চেরি ঘন্টা পায়ে, এটি অ বর্গ শিকড় পুনর্নির্মাণ করা প্রয়োজন।
4. ধাপ -1 এ Pokhіdna zminnoї
5. Pokhіdna বর্গমূল
6. Pokhіdna সাইনাস
7. পোখিদনা কোসাইন
8. Pokhіdna স্পর্শক
9. Pokhіdna cotangent
10. আর্কসিনের অনুরূপ
11. আর্কোসাইনের অনুরূপ
12. পোখিদনা আর্কটেনজেন্ট
13. Pokhіdna চাপ স্পর্শক
14. প্রাকৃতিক লগারিদমের অনুরূপ
15. রুক্ষ লগারিদমিক ফাংশন
16. Pokhіdna exponenti
17. পোখিদনা ডিসপ্লে ফাংশন

পার্থক্যের নিয়ম

1. Pokhіdna সুমি চি খুচরো
2. ভাল কাজ করুন
2ক. Pokhіdna virazi, ধ্রুবক গুণক দ্বারা গুণিত
3. ব্যক্তিগত যান
4. ভাঁজ ফাংশন

নিয়ম 1কি ফাংশন

বর্তমান বিন্দুতে পার্থক্য, তারপর পার্থক্য এবং ফাংশনের একই বিন্দুতে

কেন

tobto বীজগণিতীয় ফাংশনের অনুরূপ সমষ্টি হল অনুরূপ ফাংশনের বীজগণিতের অনুরূপ সমষ্টি।

পরিণতি। দুটি ফাংশন হিসাবে যা পার্থক্যকারী, একটি স্থায়ী সংযোজনে পুনর্নবীকরণ, তারপর তারা একই রকম, তারপর

নিয়ম 2কি ফাংশন

বর্তমান বিন্দুতে পার্থক্য করা হয়, তারপর একই বিন্দুতে, সেই অতিরিক্ত বিন্দুগুলিকে আলাদা করা হয়

কেন

tobto দুটি ফাংশনের কাজটি বাকিগুলির জন্য এই ফাংশনগুলির সাথে ত্বকের কাজের যোগফলের জন্য ভাল।

শেষ ১. খারাপ চিহ্নের জন্য ধ্রুবক গুণককে দায়ী করা যেতে পারে:

শেষ 2। Pokhіdna dekilkoh funktsіy, scho differenziyuyutsya, dobrіvnyuє tvorіvі vіdnoї kohіdnoї derzhnoi z spіvmnіnіkіv іn সব іnshі তৈরি করুন।

উদাহরণস্বরূপ, তিনটি গুণের জন্য:

নিয়ম 3কি ফাংশন

deyakіy পয়েন্ট মধ্যে পার্থক্য і , তারপর এই সময়ে এটি পার্থক্য করা হয় এবং iu/v, তাছাড়া

tobto একটি ভগ্নাংশের ব্যক্তিগত দুটি ফাংশনের অনুরূপ, সংখ্যা বইয়ের মৃত্যুর জন্য একটি ব্যানারম্যানের সৃষ্টির সংখ্যা এবং ব্যানারম্যানের মৃত্যুর জন্য ব্যানারের সংখ্যা এবং ব্যানারটি বিশাল বর্গক্ষেত্র। সংখ্যা বই।

অন্য দিকে দে শো শুকতি

যখন আপনি ভাল জিনিসগুলি জানেন, তখন এটি প্রায়শই বাস্তব পরিচালকদের কাছে করুন, অনেকগুলি পার্থক্যের নিয়মগুলি zastosovuvaty করা প্রয়োজন, তাই ভাল সময়ের জন্য আরও অ্যাপ্লিকেশন রয়েছে - পরিসংখ্যানে"আপনার নিজস্ব ব্যক্তিগত ফাংশন তৈরি করুন".

সম্মান.যোগফলের যোগের মতো ধ্রুবককে (সেই সংখ্যা) বিভ্রান্ত না করার জন্য স্লাইড করুন এবং একটি ধ্রুব গুণকের মতো! একজন ভাইপ্যাডিয়ানের জন্য, ডোডাঙ্কা її pokhіdna শূন্য থেকে বেশি ব্যয়বহুল, এবং একটি দ্রুত গুণক সময়ের জন্য, এটি pokhіdnyh চিহ্নের জন্য দায়ী করা হবে। এটি একটি সাধারণ ক্ষমা, কারণ এটি অতীতের বংশবৃদ্ধির কোব পর্যায়ে দেখা যায়, তবে বিশ্বে এটি ইতিমধ্যেই দেখা যায় কতগুলি এক-দুই-তলা স্টক। মধ্যম ছাত্র tsyu ক্ষমা আর ডাকাতি.

এবং ব্যক্তিগত সৃষ্টির পার্থক্যের জন্য, আপনার একটি সংযোজন আছে u"v, যা u- সংখ্যা, উদাহরণস্বরূপ, 2 বা 5, এটি একটি ধ্রুবক, তারপর একই সংখ্যা শূন্য i এর সমান হবে, তারপর, সমস্ত সংযোজন শূন্যের সমান হবে (বাট 10 এর ব্যবস্থা করার মতো একটি প্যাটার্ন)।

ইনশা ঘন ঘন ক্ষমা- একটি নৈমিত্তিক সাধারণ ফাংশনের মতো নৈমিত্তিক ভাঁজ ফাংশনের যান্ত্রিক সমাধান। টম ভাঁজযোগ্য ফাংশন okrem বিধি নিবেদিত. আলে, পিছনে পিছনে, আমি ভাল জানি সহজ ফাংশন.

পথ ধরে, আপনি ভিরাজ পরিবর্তন ছাড়া করতে পারবেন না। যাদের জন্য আপনার নতুন উইন্ডোজের সাহায্যের প্রয়োজন হতে পারে Dії zі ধাপ এবং শিকড়і ভগ্নাংশ সহ Dії .

কিভাবে আপনি পদক্ষেপ এবং শিকড় সঙ্গে অনুরূপ ভগ্নাংশ সমাধান খুঁজে না, তাই যদি ফাংশন তাকান করতে পারেন , তারপর পাঠটি অনুসরণ করুন "পদক্ষেপ এবং শিকড় সহ শটগুলির একটি ব্যাগ থাকা ভাল।"

যক্ষ্‌চো তোর আগে ভালোভাবে নাচেবতো zavdannya , তাহলে আপনি "Vyrobnі সহজ ত্রিকোণমিতিক ফাংশন" নিয়ে ব্যস্ত।

পোকরোকোভি বাটস - আমি যাচ্ছি কিনা জানব কিভাবে

উদাহরণ 3।সম্পর্কিত ফাংশন জানুন

সমাধান। এটা স্পষ্ট যে ভাইরাসেজের একটি অংশ কাজ করে: সম্পূর্ণ ভাইরাসজ টিভিরকে প্রতিনিধিত্ব করে, যেমন গুণক - সুমি, অন্যটির একটি অতিরিক্ত গুণক রয়েছে। সৃষ্টির জন্য পার্থক্যের একটি নির্দিষ্ট নিয়ম রয়েছে: দুটি ফাংশন আরও সুন্দরভাবে তৈরি করুন, ত্বক সৃষ্টির যোগফল এবং বাকিগুলির জন্য এই ফাংশনগুলি:

আমরা যোগফলের পার্থক্যের একটি স্থিতিশীল নিয়ম দিয়েছি: বীজগণিতীয় ফাংশনের যোগফল অনুরূপ ফাংশনের বীজগণিতের যোগফলের সমান। স্কিন ব্যাগে আমাদের মন একটি বিয়োগ চিহ্ন সহ আরেকটি সংযোজন আছে। ত্বকের সমষ্টিতে, অনেক স্বাধীন পরিবর্তন আছে, এটি একটি স্বাস্থ্যকরের মতো, এবং একটি ধ্রুবক (সংখ্যা) যা শূন্যের মতো। Otzhe, "iks" আমাদের সাথে রূপান্তরিত হয় এক, এবং বিয়োগ 5 - শূন্যে। অন্য ক্ষেত্রে, "iks" কে 2 দ্বারা গুণ করা হয়, তাই দুটি একই এক দ্বারা গুণ করা হয়, যেমন "iks" চলে গেছে। আমরা নিম্নলিখিত মানগুলি কেড়ে নিই:

আসুন কল্পনা করি যে সৃজনশীলের যোগফল সমস্ত ফাংশনের জন্য মনের প্রয়োজনীয়তা খুঁজে পেয়েছে:

এবং ভবিষ্যতের জন্য কাজের বিকাশকে বিপরীত করা সম্ভব।

বাট 4।সম্পর্কিত ফাংশন জানুন

সমাধান। আমাদের গোপনীয়তা জানা আবশ্যক। Zastosovuєmo সূত্র diferentiyuvannya chastki: pokhіdna chastki dvoh funktsіy dorіvnyuє ভগ্নাংশ, সংখ্যার মৃত্যুর জন্য ব্যানারের সৃষ্টির এই ধরনের পার্থক্যের সংখ্যা এবং ব্যানারের মৃত্যুর জন্য সংখ্যা, এবং ব্যানারটি সংখ্যার বর্গক্ষেত্র। সংখ্যা আমরা নেবো:

আমরা ইতিমধ্যেই বাট 2 এ জানতাম। আসুন ভুলে গেলে চলবে না যে এটি সত্য, স্ট্রিমিং বাটে নম্বর বইতে আরেকটি sp_multiplier একটি বিয়োগ চিহ্ন সহ নেওয়া হয়েছে:

আপনি এই ধরনের কাজের বহুমুখিতাকে কীভাবে দেখেন, যেখানে আপনাকে সঠিক ফাংশনগুলি জানতে হবে, সেই ধাপগুলির শিকড়গুলিকে সঞ্চয় করতে হবে, যেমন, উদাহরণস্বরূপ, , তারপর অনুগ্রহ করে একটি চাকরির জন্য জিজ্ঞাসা করুন "কদম এবং শিকড় সহ বীরবনা সুমি শট" .

ঠিক আছে, আপনাকে আরও খারাপ সাইন, কোসাইন, স্পর্শক এবং অন্যান্য সম্পর্কে আরও জানতে হবে ত্রিকোণমিতিক ফাংশন, তারপর, যদি ফাংশন দেখতে পারেন , তাহলে আপনার কাছে একটি পাঠ আছে "সম্পূর্ণ সহজ ত্রিকোণমিতিক ফাংশন" .

উদাহরণ 5।সম্পর্কিত ফাংশন জানুন

সমাধান। এই ফাংশনের একটি bachimo tver আছে, তাদের মধ্যে একটি সাধারণ গুণক হল স্বাধীন পরিবর্তনের বর্গমূল, একটি অনুরূপ একটির সাথে আমরা অনুরূপের টেবিল থেকে জানতে পেরেছি। পার্থক্যের নিয়মের পিছনে, একই বর্গমূলের সেই ট্যাবুলার মান তৈরি করা হয়:

ভবিষ্যতের জন্য টাস্কের সমাধানের পুনর্বিবেচনা করা সম্ভব অনলাইন ক্যালকুলেটর .

উদাহরণ 6.সম্পর্কিত ফাংশন জানুন

সমাধান। এই ফাংশনটি আরও ব্যক্তিগত, যেকোনোটির দূরত্ব স্বাধীন পরিবর্তনের বর্গমূল। প্রাইভেট এর পার্থক্যের নিয়মের পিছনে, যেমন আমরা এটিকে পুনরাবৃত্তি করেছি এবং প্রয়োগ 4 এ রাখি, অনুরূপ বর্গমূলের সারণী মানটি নেওয়া হয়:

সংখ্যা বইয়ের একটি ভগ্নাংশ নিতে, আমরা সংখ্যা বই এবং ব্যানারকে দ্বারা গুণ করি।

ভাঁজ করার ফাংশনগুলি মনোনীত ফোল্ডিং ফাংশনের জন্য নিয়মিত ফিট মত দেখায়। যদি এটি y \u003d sin x - (2 - 3) a rct g x x 5 7 x 10 - 17 x 3 + x - 11 ফর্মের একটি ফাংশন হয়, তাহলে її y \u003d sin 2 x ভিউতে সংকোচিত হতে পারে না।

এই নিবন্ধটি ভাঁজ ফাংশন এবং প্রকাশ বোঝার দেখাবে। visnovka সমাধান এর বাট থেকে অনুরূপ তাত্পর্য সূত্র সঙ্গে সংশোধন। খারাপের Zastosuvannya টেবিল এবং পার্থক্য নিয়ম লক্ষণীয়ভাবে খারাপ পরিবর্তনের জন্য ঘন্টা পরিবর্তন.

প্রধান অ্যাপয়েন্টমেন্ট

নিয়োগ 1

একটি কলাপসিবল ফাংশন যেমন একটি ফাংশন বিবেচনা করে, ঠিক যেমন আর্গুমেন্টও একটি ফাংশন।

এটি নিম্নরূপ মনোনীত করা হয়েছে: f (g (x))। এটা সম্ভব যে ফাংশন g(x) যুক্তি f(g(x)) দ্বারা বিবেচনা করা হয়।

নিয়োগ 2

একইভাবে, ফাংশন f এবং є cotangent এর ফাংশন, তারপর g(x) = ln x হল প্রাকৃতিক লগারিদমের ফাংশন। মনে রাখবেন যে সংকোচনযোগ্য ফাংশন f(g(x)) arctg(lnx) হিসাবে লেখা যেতে পারে। কিন্তু ফাংশন f, যা 4টি ধাপের একটি ফাংশন, de g (x) \u003d x 2 + 2 x - 3 পুরো মূলদ ফাংশন দ্বারা বিবেচনা করা হয়, আমরা ধরে নিই যে f (g (x)) \u003d ( x 2 + 2 x - 3) 4।

এটা স্পষ্ট যে g(x) কলাপসিবল হতে পারে। বাট y \u003d sin 2 x + 1 x 3 - 5 থেকে এটা স্পষ্ট যে g এর মান হতে পারে ঘনমূলএকটি ভগ্নাংশ সঙ্গে. ডেনিশ ভিরাজকে y \u003d f (f 1 (f 2 (x))) হিসাবে চিহ্নিত করা যেতে পারে। তারা হতে পারে যে f সাইনের ফাংশন, এবং f 1 হল ফাংশন যা বর্গমূলের নীচে প্রসারিত হয়, f 2 (x) \u003d 2 x + 1 x 3 - 5 একটি ভগ্নাংশ মূলদ ফাংশন।

নিয়োগ 3

অবদানের হার কিছু স্বাভাবিক সংখ্যা হিসাবে নির্ধারিত হয় এবং y = f (f 1 (f 2 (f 3 (... (f n (x))))))) হিসাবে লেখা হয়।

নিয়োগ 4

ফাংশনের গঠন বোঝা মানসিক টাস্কের জন্য ইনপুট ফাংশনের সংখ্যার উপর নির্ভর করে। বিজয়ের পরিপূর্ণতার জন্য, মনের ভাঁজ ফাংশনের মিলের সূত্র

(f(g(x))) "=f"(g(x)) g"(x)

আবেদন করুন

বাট 1

y = (2 x + 1) 2 ফর্মের একটি ভাঁজ ফাংশন খুঁজুন।

সমাধান

মনের পিছনে দেখা যায় যে f হল একটি বর্গাকার ফাংশন এবং g (x) \u003d 2 x + 1 একটি রৈখিক ফাংশন দ্বারা বিবেচনা করা হয়।

আসুন ভাঁজ ফাংশনের জন্য একটি অনুরূপ সূত্র তৈরি করুন এবং এটি লিখুন:

f "(g(x)) = ((g(x)) 2)" = 2 (g(x)) 2 - 1 = 2 g(x) = 2 (2x + 1); g "(x) = (2 x + 1)" = (2 x) "+ 1" = 2 x " + 0 = 2 1 x 1 - 1 = 2 ⇒ (f (g (x))) "=f "(g(x)) g"(x) = 2 (2x + 1) 2 = 8x + 4

বাহ্যিক লুকিং ফাংশনটি কীভাবে সরল করা যায় তা জানা দরকার। আমরা নেবো:

y = (2x + 1) 2 = 4x2 + 4x + 1

Zvіdsi maєmo, scho

y"=(4x2+4x+1)"=(4x2)"+(4x)"+1"=4(x2)"+4(x)"+0==4 2 x 2 - 1 + 4 1 x 1 - 1 = 8 x + 4

ফলাফল তীর্যক ছিল.

এই ধরনের একটি কাজ সম্পাদন করার সময়, এটি বোঝা গুরুত্বপূর্ণ, ফর্ম f і g (x) এর de-roztashovuvatimeet ফাংশন।

বাট 2

y = sin 2 x এবং y = sin x 2 ফর্মের জটিল ভাঁজ ফাংশনগুলি জানতে পরবর্তী।

সমাধান

ফাংশনের প্রথম এন্ট্রিটি মিলাতে হবে যে f হল বর্গ ফাংশন, এবং g (x) হল সাইন ফাংশন। তোদি ওট্রিমাইমো যে

y "= (sin 2 x)" = 2 sin 2 - 1 x (sin x)" = 2 sin x cos x

আরেকটি স্বরলিপি দেখায় যে f একটি সাইন ফাংশন, এবং g(x) = x 2 অর্থপূর্ণ শহুরে উৎসব. মনে হচ্ছে অতিরিক্ত কোলাপসিবল ফাংশন হিসাবে লেখা হবে

y " \u003d (sin x 2) " \u003d cos (x 2) (x 2) " \u003d cos (x 2) 2 x 2 - 1 \u003d 2 x cos (x 2)

এলোমেলো y \u003d f (f 1 (f 2 (f 3 (... (fn (x))))))) এর সূত্রটি y "= f" (f 1 (f 2 (f 3) হিসাবে লেখা হয়েছে (. ... .) fn (x)))))) f 1 "(f 2 (f 3 (. . . (fn (x)))))) f 2 " (f 3 (... . (fn) (x)))))। . . f n "(x)

বাট 3

একটি অনুরূপ ফাংশন y = sin (ln 3 a r c t g (2 x)) খুঁজুন।

সমাধান

ড্যানিশ বাট রেকর্ডের ভাঁজ এবং ফাংশন সম্প্রসারণের উপাধি দেখায়। তারপর y \u003d f (f 1 (f 2 (f 3 (f 4 (x)))))) তাৎপর্যপূর্ণ, de f , f 1 , f 2 , f 3 , f 4 (x) 3 ধাপ, একটি ফাংশন একটি লগারিদম এবং একটি বেস e সহ, চাপ স্পর্শকের একটি ফাংশন এবং একটি রৈখিক একটি।

একটি সঙ্কুচিত ফাংশনের উপাধির জন্য 3টি সূত্র

y "= f "(f 1 (f 2 (f 3 (f 4 (x))))) f 1 "(f 2 (f 3 (f 4 (x)))) f 2 "( f 3 (f 3 ( f 4 (x))) f 3 "(f 4 (x)) f 4 "(x)

আমাদের যা জানা দরকার তা আমরা গ্রহণ করি

1. f "(f 1 (f 2 (f 3 (f 4 (x)))))) = cos (ln 3 arctg (2x))।
2. f 1 "(f 2 (f 3 (f 4 (x)))) (2 x) = 3 ln 2 arctg (2 x)।
3. f 2 "(f 3 (f 4 (x))) একইভাবে লগারিদমিক, তারপর f 2 "(f 3 (f 4 (x))) = 1 a r c t g (2 x)।
4. f 3 "(f 4 (x)) একটি অনুরূপ চাপ স্পর্শক হিসাবে, তারপর f 3 "(f 4 (x)) \u003d 1 1 + (2 x) 2 \u003d 1 1 + 4 x 2।
5. একটি উল্লেখযোগ্য f 4 (x) \u003d 2 x এর সাথে, একটি সূচক সহ একটি অনুরূপ স্ট্যাটিক ফাংশনের চিহ্নের জন্য অপরাধ 2 আছে যা ভাল 1 তারপর f 4 "(x) \u003d (2 x)" \u003d 2 x "= 2 1 x 1 - 1 = 2।

আমরা মধ্যবর্তী ফলাফলের একটি সারসংক্ষেপ বহন করি এবং আমরা তা বিবেচনা করি

y "= f "(f 1 (f 2 (f 3 (f 4 (x))))) f 1 "(f 2 (f 3 (f 4 (x)))) f 2 "( f 3 (f 3 ( f 4 (x))) f 3 "(f 4 (x)) f 4 "(x) = cos (ln 3 arctan (2 x)) 3 ln 2 আর্কটান (2 x) 1 আর্কটান (2 x) 1 1 + 4 x 2 2 = = 6 cos (ln 3 আর্কটান (2 x)) ln 2 আর্কটান (2 x) আর্কটান (2 x) (1 + 4 x 2 )

এই ধরনের ফাংশন বিশ্লেষণ matrioshkas করা হবে. পার্থক্যের নিয়ম সবসময় স্থির করা যায় না স্পষ্টআরও খারাপের টেবিলের সাহায্যের জন্য। প্রায়শই, অনুরূপ ভাঁজ ফাংশনগুলির তাত্পর্যের জন্য সূত্রটি লিখতে হবে।

Іsnuyut deyakі vіdminnostі ভাঁজযোগ্য ফাংশন ভাঁজ করা যায়। একটি পরিষ্কার মননশীলতার সাথে, বিশেষ করে খারাপগুলিকে চিনতে সহজ।

বাট 4

এমন বাটের নিশানা দেখতে হবে। যদি এটি y \u003d tg 2 x + 3 tgx + 1 ফর্মের একটি ফাংশন হয়, তবে এটিকে একটি ভাঁজ আকার g (x) \u003d tgx, f (g) \u003d g 2 + 3 g + 1 হিসাবে দেখা যেতে পারে . এটা স্পষ্ট যে একটি ভাঁজ সূত্রের জন্য সূত্রগুলি আঁকতে হবে:

f "(g (x)) = (g 2 (x) + 3 g (x) + 1)" = (g 2 (x)) "+ (3 g (x))" + 1 " == 2 g 2 - 1 (x) + 3 g "(x) + 0 \u003d 2 g (x) + 3 1 g 1 - 1 (x) \u003d \u003d 2 g (x) + 3 \u003d 2 tgx + 3; g " (x) = (tgx) " = 1 cos 2 x ⇒ y " = (f (g (x)) " = f " (g (x)) g " (x) = (2 tgx + 3 ) 1 cos 2 x = 2 tanx + 3 cos 2 x

y = t g x 2 + 3 t g x + 1 ফর্মের একটি ফাংশন সংকোচনযোগ্য বলে বিবেচিত হয় না; যাইহোক, t g x 2 একটি ভাঁজ ফাংশন হিসাবে বিবেচিত হয়, তারপর g (x) = x 2 і f ফর্মের একটি স্ট্যাটিক ফাংশন একটি স্পর্শক ফাংশন। কার জন্য ব্যাগ দ্বারা পার্থক্য করা উচিত. আমরা সেটা মেনে নিই

y " = (tgx 2 + 3 tgx + 1) " = (tgx 2) " + (3 tgx) " + 1 " == (tgx 2) " + 3 (tgx) " + 0 = (tgx 2) " + 3 কারণ 2 x

চলুন একটি অনুরূপ ভাঁজ ফাংশনের মান (t g x 2) ":

f "(g (x)) \u003d (tg (g (x))" \u003d 1 cos 2 g (x) \u003d 1 cos 2 (x 2) g "(x) \u003d (x 2)" \u003d 2 x 2 - 1 \u003d 2 x ⇒ (tgx 2) "= f "(g (x)) g "(x) \u003d 2 x cos 2 (x 2)

আমরা y নিই "= (t g x 2 + 3 t g x + 1)" = (t g x 2) "+ 3 cos 2 x = 2 x cos 2 (x 2) + 3 cos 2 x

ভাঁজ ফাংশন ভাঁজ ফাংশন আগে অন্তর্ভুক্ত করা যেতে পারে, এবং ভাঁজ ফাংশন নিজেদের গুদাম ভাঁজ ফাংশন হতে পারে.

বাট 5

উদাহরণস্বরূপ, আসুন y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x (x 2 + 1) ফর্মের সংকোচনযোগ্য ফাংশনটি দেখি।

এই ফাংশনটিকে y = f (g (x)) হিসাবে উপস্থাপন করা যেতে পারে, যেখানে f এর মান হল বেস 3 এর লগারিদমের একটি ফাংশন, এবং g (x) কে h ফর্মের দুটি ফাংশনের যোগফল হিসাবে নেওয়া হয় ( x) = x 2 + 3 cos 3 (2 x + 1) + 7 ex 2 + 3 3 i k(x) = ln 2 x (x 2 + 1)। স্পষ্টতই, y = f(h(x) + k(x))।

আসুন h(x) ফাংশনটি দেখি। দাম l (x) \u003d x 2 + 3 cos 3 (2 x + 1) + 7 থেকে m (x) \u003d e x 2 + 3 3

হতে পারে l(x) \u003d x 2 + 3 cos 2 (2 x + 1) + 7 \u003d n (x) + p (x) - দুটি ফাংশনের যোগফল n (x) \u003d x 2 + 7 এবং p (x) \u003d 3 cos 3 (2 x + 1) , de p (x) \u003d 3 p 1 (p 2 (p 3 (x))) হল একটি ভাঁজ ফাংশন যার একটি সংখ্যাসূচক সহগ 3 এবং p 1 হল একটি কিউব ফাংশন, p 2 কোসাইন ফাংশন, p 3 (x) = 2 x + 1 - লিনিয়ার ফাংশন।

আমরা সরিয়ে নিয়েছি যে m(x) = ex 2 + 3 3 = q (x) + r (x) - দুটি ফাংশনের যোগফল q (x) = ex 2 і r (x) = 3 3 de q (x) = q 1 (q 2 (x)) একটি কোলাপসিবল ফাংশন, q 1 একটি সূচক সহ একটি ফাংশন, q 2 (x) = x 2 একটি স্টেট ফাংশন।

দেখা যায় যে h (x) = l (x) m (x) = n (x) + p (x) q (x) + r (x) = n (x) + 3 p 1 (p 2 ( p 3 (x))) q 1 (q 2 (x)) + r (x)

k(x) = ln 2 x (x 2 + 1) = s (x) t (x) ফর্মটির দৃশ্যে পাস করার সময়, এটি স্পষ্ট যে ফাংশনটি s(x) = ভাঁজ আকারে উপস্থাপন করা হয়েছে ln 2 x = s 1 ( s 2 (x)) একটি মূলদ সংখ্যা t (x) \u003d x 2 + 1, de s 1 є স্কোয়ারিং ফাংশন, এবং s 2 (x) \u003d ln x - বেস e সহ লগারিদমিক .

দেখে মনে হচ্ছে আমি k (x) = s (x) t (x) = s 1 (s 2 (x)) t (x) দেখতে যাচ্ছি।

তোদি ওট্রিমাইমো যে

y = লগ 3 x 2 + 3 cos 3 (2 x + 1) + 7 ex 2 + 3 3 + ln 2 x (x 2 + 1) = = fn (x) + 3 p 1 (p 2 (p 3) x))) q 1 (q 2 (x)) = r (x) + s 1 (s 2 (x)) t (x)

ফাংশনের কাঠামোর পিছনে, এটি স্পষ্ট হয়ে গেছে যে পার্থক্যের জন্য অভিব্যক্তিকে সরল করার জন্য কীভাবে এবং কীভাবে সূত্রগুলি ঠিক করা দরকার। এই ধরনের কাজগুলি জানতে এবং সেগুলি বোঝার জন্য, ফাংশনের পার্থক্যের বিন্দুতে ফিরে যাওয়া প্রয়োজন, যা গুরুত্বপূর্ণ।

যেন আপনি পাঠ্যটিতে ক্ষমার কথা মনে রেখেছেন, দয়ালু হন, এটি দেখুন এবং Ctrl + এন্টার টিপুন

একটি ভাঁজযোগ্য ফাংশন সম্পর্কে প্রথম উপপাদ্য, যা নিম্নরূপ প্রণয়ন করা হয়েছে:

চলুন 1) ফাংশন $u=\varphi (x)$ এর প্রথম পয়েন্টে $u_(x)"=\varphi"(x_0)$ থাকতে পারে $x_0$; 2) ফাংশন $y=f(u)$ পরিবর্তন হতে পারে $y_(u)"=f"(u)$ সবচেয়ে সাম্প্রতিক পয়েন্ট $u_0=\varphi (x_0)$ এর জন্য। একইভাবে, অনুমান বিন্দুতে সংকোচনযোগ্য ফাংশন $y=f\left(\varphi (x) \right)$টিও একই রকম, অনুরূপ ফাংশন $f(u)$ এবং $\varphi (x) এর অতিরিক্ত প্রক্রিয়াকরণের সমান $:

$$ \left(f(\varphi (x))\right)"=f_(u)"\left(\varphi (x_0) \right)\cdot \varphi"(x_0) $$

অন্যথায়, একটি বড় শর্টহ্যান্ডের জন্য: $y_(x)"=y_(u)"\cdot u_(x)"$।

যে বাটে আমি ভাগ করেছি সব ফাংশন $y=f(x)$ দেখতে পারে (তাই আমরা শুধুমাত্র একটি পরিবর্তনের ফাংশন দেখতে পারি $x$)। স্পষ্টতই, সমস্ত স্টকে $x$ পরিবর্তনের জন্য $y"$ নেওয়া ভুল। উদাহরণস্বরূপ, যারা $x$ পরিবর্তন করতে স্মার্ট তারা প্রায়শই $y"$ এর পরিবর্তে $y"_x$ ব্যবহার করে।

বাট নং 1, নং 2 এবং নং 3 এ, ভাঁজ ফাংশন বোঝার প্রক্রিয়ার উপর একটি প্রতিবেদন তৈরি করা হয়েছিল। বাট নং 4 নিয়োগের একটি বৃহত্তর বোঝার টেবিল এবং বুদ্ধিমান হতে পারে.

Bazhano বাট নং 1-3 উপাদান এম্বেড করার পরে, বাট নং 5, নং 6 এবং 7 নং বাট জন্য একটি স্বাধীন সমাধান যান. একটি সংক্ষিপ্ত সিদ্ধান্ত নিতে নং 5, নং 6 এবং নং 7 প্রয়োগ করুন, যাতে পাঠক অবিলম্বে তার ফলাফলের সঠিকতা পরীক্ষা করতে পারে।

বাট #1

একটি অনুরূপ ফাংশন খুঁজুন $y=e^(\cos x)$।

আমাদের সঠিক ফোল্ডিং ফাংশন $y"$ জানতে হবে। যদি $y=e^(\cos x)$, তাহলে $y"=\left(e^(\cos x)\right)"$। জানতে ট্রিক $ \ left(e^(\cos x)\right)"$ অনুরূপ টেবিল থেকে সূত্র নং 6 জয় করুন। সূত্র #6 জেতার জন্য, আমাদের দৃষ্টিতে $u=\cos x$ কী তা সংশোধন করা প্রয়োজন। আরও, সিদ্ধান্তটি $u$ এর পরিবর্তে $\cos x$ করার জন্য সূত্র নং 6-এর সাধারণ সাবস্টেশনগুলিতে প্রয়োগ করা হয়:

$$ y"=\left(e^(\cos x) \right)"=e^(\cos x)\cdot (\cos x)" \tag (1.1)$$

এখন $(\cos x)"$ virase-এর মান জানতে হবে। আসুন নীচের টেবিলে ফিরে যাই, এর থেকে সূত্র নং 10 বেছে নেওয়া যাক। সূত্র নং 10-এর জন্য $u=x$ প্রতিস্থাপন করা, হতে পারে: $(\cos x)"=-\ sin x\cdot x"$। এখন সমতা চালিয়ে যাওয়া যাক (1.1), এটি যোগ করার পরে, আমরা ফলাফলটি খুঁজে পাই:

$$ y"=\left(e^(\cos x) \right)"=e^(\cos x)\cdot (\cos x)"= e^(\cos x)\cdot (-\sin x \cdot x") \tag (1.2) $$

Skіlki $x"=1$, তাহলে আমরা সমতা চালিয়ে যেতে পারি (1.2):

$$ y"=\left(e^(\cos x) \right)"=e^(\cos x)\cdot (\cos x)"= e^(\cos x)\cdot (-\sin x \cdot x")=e^(\cos x)\cdot (-\sin x\cdot 1)=-\sin x\cdot e^(\cos x) \tag (1.3) $$

এছাড়াও, প্যারিটি থেকে (1.3) হতে পারে: $y"=-\sin x\cdot e^(\cos x)$। 1.3) পরে, একটি অনুরূপ কোলাপসিবল ফাংশন পাওয়া গেছে;

ভিডপোভিড: $y"=-\sin x\cdot e^(\cos x)$।

বাট #2

নিম্নলিখিত ফাংশনগুলি খুঁজুন $y=9\cdot \arctg^(12)(4\cdot \ln x)$।

আমাদের খরচ হিসাব করতে হবে $y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"$। এটা তাৎপর্যপূর্ণ যে ধ্রুবক (এটি 9 নম্বর) খারাপ চিহ্নের জন্য দায়ী করা যেতে পারে:

$$ y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"=9\cdot\left(\arctg^(12)(4\cdot \ln x) \right)" \tag (2.1) $$

এখন চলুন virase $\left(\arctg^(12)(4\cdot \ln x) \right)"$। অনুরূপ সারণী থেকে একটি সূত্র বেছে নেওয়ার জন্য, এটা সহজ, আমি করব virase উপস্থাপন করুন, যা দেখতে এইরকম: $\ left( \left(\arctg(4\cdot \ln x) \right)^(12)\right)"$। এখন এটা স্পষ্ট যে 2 নং ফর্মুলা জিততে হবে, টবটো। $\left(u^\alpha \right)"=\alpha\cdot u^(\alpha-1)\cdot u"$। Qiu-এর জন্য, সূত্রটি $u=\arctg(4\cdot \ln x)$ i $\alpha=12$ দ্বারা উপস্থাপন করা যেতে পারে:

সমতা পরিপূরক (2.1) ফলাফল থেকে বিয়োগ করা হয়, সম্ভবত:

$$ y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"=9\cdot\left(\arctg^(12)(4\cdot \ln x) \right)"= 108\cdot\left(\arctg(4\cdot \ln x) \right)^(11)\cdot (\arctg(4\cdot \ln x))" \tag (2.2) $$

এই পরিস্থিতিতে, একটি ক্ষমা প্রায়ই অনুমোদিত হয়, যদি প্রথম পছন্দটি সূত্র হয় $(\arctg \; u)"=\frac(1)(1+u^2)\cdot u"$ $\left সূত্রটি প্রতিস্থাপন করুন (u^\ alpha \right)"=\alpha\cdot u^(\alpha-1)\cdot u"$। ডানদিকে, প্রথম জিনিস দোষারোপ করা হয়, কিন্তু pokhіdna zvnіshnyої ফাংশনসії। বোঝার জন্য, যেমন ফাংশনটি নিজেই $\arctg^(12)(4\cdot 5^x)$ এর জন্য বলা হবে, দেখান যে আপনি $\arctg^(12)(4\cdot 5^) এর মান সম্পর্কে যত্নশীল x)$ $x$ এর যেকোনো মানের জন্য। $5^x$ এর মান অনুমান করে শুরু করুন, তারপর $4\cdot 5^x$ বিয়োগ করে ফলাফলটিকে 4 দ্বারা গুণ করুন। এখন, ফলাফল দেওয়া হলে, আমরা $arctg(4cdot 5^x)$ বিয়োগ করে arctangent নিই। তারপরে আমরা $ arctg (12) (4 cdot 5 x) $ বিয়োগ করে বারোটি ধাপে সংখ্যাটি নিই। দূরে থাকো, - তোবতো। 12 ধাপে zvedennya - এবং একই ফাংশন হবে। এবং পরের জিনিসটি ছিল একটি তিরস্কার শুরু করা, যা সমতা দ্বারা ভাঙ্গা হয়েছিল (2.2)।

এখন এটা জানা দরকার $(\arctg(4\cdot \ln x)"$। আমরা এর মধ্যে $u=4\cdot \ln x$ প্রতিস্থাপন করে অনুরূপ টেবিলের 19 নং সূত্র জিততে পারি:

$$ (\arctg(4\cdot \ln x))"=\frac(1)(1+(4\cdot \ln x)^2)\cdot (4\cdot \ln x)" $$

Viraz, vrahovoyuchi $(4\cdot \nn x)^2=4^2\cdot (\ln x)^2=16\cdot \ln^2 x$ থেকে ট্রচগুলি সহজেই বিয়োগ করা যেতে পারে।

$$ (\arctg(4\cdot \ln x))"=\frac(1)(1+(4\cdot \ln x)^2)\cdot (4\cdot \ln x)"=\frac( 1)(1+16\cdot \ln^2 x)\cdot (4\cdot \ln x)" $$

সমতা (2.2) এখন এইরকম হবে:

$$ y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"=9\cdot\left(\arctg^(12)(4\cdot \ln x) \right)"=\\ =108\cdot\left(\arctg(4\cdot \ln x) \right)^(11)\cdot (\arctg(4\cdot \ln x))"=108\cdot \left(\arctg(4\cdot \ln x) \right)^(11)\cdot \frac(1)(1+16\cdot \ln^2 x)\cdot (4\cdot \ln x)" \ ট্যাগ (2.3) $$

$(4\cdot \ln x)"$ জানার জন্য এটি আর যথেষ্ট নয়। খারাপ চিহ্নের জন্য আমরা ধ্রুবককে (যা 4) দায়ী করি: $(4\cdot \ln x)"=4\cdot (\ln x)"$. জানার জন্য $(\ln x)"$ এর মধ্যে $u=x$ প্রতিস্থাপন করে সূত্র #8 জিতুন: $(\ln x)"=\frac(1)(x)\cdot x"$। যদি $x"=1$, তাহলে $(\ln x)"=\frac(1)(x)\cdot x"=\frac(1)(x)\cdot 1=\frac(1)(x) $। সূত্র (2.3) থেকে ফলাফল বিয়োগ করার পরে, আমরা বিয়োগ করি:

$$ y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"=9\cdot\left(\arctg^(12)(4\cdot \ln x) \right)"=\\ =108\cdot\left(\arctg(4\cdot \ln x) \right)^(11)\cdot (\arctg(4\cdot \ln x))"=108\cdot \left(\arctg(4\cdot \ln x) \right)^(11)\cdot \frac(1)(1+16\cdot \ln^2 x)\cdot (4\cdot \ln x)" =\\ =108\cdot \left(\arctg(4\cdot \ln x) \right)^(11)\cdot \frac(1)(1+16\cdot \ln^2 x)\cdot 4\ cdot \frac(1)(x)=432\cdot \frac(\arctg^(11)(4\cdot \ln x))(x\cdot (1+16\cdot \ln^2 x)))।$

আমি অনুমান করছি যে ভাঁজ ফাংশনগুলি প্রায়শই এক সারিতে পাওয়া যায় - যেমনটি বাকি সমতায় লেখা হয়। অতএব, সাধারণ rozrahunkіv বা নিয়ন্ত্রণ রোবট আঁকার সময়, এই ধরনের বিশদভাবে সমাধানটি আঁকা বাধ্যতামূলক নয়।

ভিডপোভিড: $y"=432\cdot \frac(\arctg^(11)(4\cdot \ln x))(x\cdot (1+16\cdot \ln^2 x))$।

বাট #3

$y"$ ফাংশন $y=\sqrt(\sin^3(5\cdot9^x))$ জানুন।

cob ট্রকের জন্য, আমরা একই ধাপে র্যাডিকাল (মূল) যোগ করে $y$ ফাংশন পরিবর্তন করি: $y=\sqrt(\sin^3(5\cdot9^x))=\left(\sin(5\) cdot 9^x) \right)^(\frac(3)(7))$। এবার আসা যাক খারাপ বিষয়ে। $y=\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))$, তারপর:

$$ y"=\left(\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))\right)" \tag (3.1) $$

অনুরূপ সারণী থেকে 2 নং ফর্মুলা জয় করা, এতে প্রতিস্থাপন করা $u=\sin(5\cdot 9^x)$ i $\alpha=\frac(3)(7)$:

$$ \left(\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))\right)"= \frac(3)(7)\cdot \left( \sin(5\cdot 9^x)\right)^(\frac(3)(7)-1) (\sin(5\cdot 9^x))"=\frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) (\sin(5\cdot 9^x))" $$

Prodovzhimo rivnist (3.1), vikoristuyuchi ফলাফল বিয়োগ:

$$ y"=\left(\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))\right)"=\frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) (\sin(5\cdot 9^x))" \tag (3.2) $$

এখন এটা জানা দরকার $(\sin(5\cdot 9^x))"$। $u=5\cdot 9^x$ প্রতিস্থাপন করে অনুরূপদের টেবিল থেকে 9 নং সূত্র জয় করা সম্ভব। এটা:

$$ (\sin(5\cdot 9^x))"=\cos(5\cdot 9^x)\cdot(5\cdot 9^x)" $$

ফলাফলে সমতা (3.2) যোগ করে, আমরা করতে পারি:

$$ y"=\left(\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))\right)"=\frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) (\sin(5\cdot 9^x))"=\\ =\frac(3) (7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) \cos(5\cdot 9^x)\cdot(5\cdot 9 ^x)" \ ট্যাগ (3.3) $$

$(5\cdot 9^x)"$ জানতে ভুলে গেছি। কোবের জন্য আমরা ধ্রুবককে ($5$ সংখ্যা) অনুরূপ চিহ্নের জন্য দায়ী করি, তারপর $(5\cdot 9^x)"=5\cdot (9^x) "$। অনুরূপ $(9^x)"$ এর মানের জন্য, আমরা $a=9$ এবং $u=x প্রতিস্থাপন করে অনুরূপ টেবিলের 5 নম্বর সূত্র তৈরি করব। $ এর আগে: $(9^x)"=9^x\cdot \ ln9\cdot x"$। যদি $x"=1$ হয়, তাহলে $(9^x)"=9^x\cdot \ln9\cdot x"=9^x\cdot \ln9$। এখন আমরা সমতা নিয়ে চলতে পারি (3.3):

$$ y"=\left(\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))\right)"=\frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) (\sin(5\cdot 9^x))"=\\ =\frac(3) (7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) \cos(5\cdot 9^x)\cdot(5\cdot 9 ^x)"= \frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) \cos(5\cdot 9 ^x)\cdot 5\cdot 9^x\cdot \ln9=\\ =\frac(15\cdot \ln 9)(7)\cdot \left(\sin(5\cdot 9^x)\right) ^(-\frac(4)(7))\cdot \cos(5\cdot 9^x)\cdot 9^x। $$

আপনি $\left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7))$ লিখে $\frac লেখার মাধ্যমে ধাপগুলিকে আবার র্যাডিকেল (এটি রুট) তে পরিণত করতে পারেন (1 )(\left(\sin(5\cdot 9^x)\right)^(\frac(4)(7)))=\frac(1)(\sqrt(\sin^4(5\) cdot 9 ^x)))$। তারপরে এটি এই ফর্মটিতে লেখা হবে:

$$ y"=\frac(15\cdot \ln 9)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7))\cdot \cos(5\cdot 9^x)\cdot 9^x= \frac(15\cdot \ln 9)(7)\cdot \frac(\cos (5\cdot 9^x)\cdot 9^x) (\sqrt(\sin^4(5\cdot 9^x))).$$

ভিডপোভিড: $y"=\frac(15\cdot \ln 9)(7)\cdot \frac(\cos (5\cdot 9^x)\cdot 9^x)(\sqrt(\sin^4(5\) ) cdot 9^x)))$।

বাট #4

দেখাও যে টেবিলের নং 3 এবং নং 4 সূত্রগুলি একই রকম এবং সারণীগুলির নং 2 সূত্রের শেষগুলি।

নিচের টেবিলের সূত্র নং 2 এর একটি অনুরূপ ফাংশন $u^\alpha$ আছে। সূত্র নং 2 এর জন্য $\alpha=-1$ প্রতিস্থাপন করে, আমরা নিই:

$$(u^(-1))"=-1\cdot u^(-1-1)\cdot u"=-u^(-2)\cdot u"\tag (4.1)$$

যদি $u^(-1)=\frac(1)(u)$ i $u^(-2)=\frac(1)(u^2)$, তাহলে সমতা (4.1) এভাবে আবার লেখা যেতে পারে: $ \ left(\frac(1)(u) \right)"=-\frac(1)(u^2)\cdot u"$। Tse এবং є সূত্র নং 3 একই রকমের টেবিল।

আমি znovnemosya নং ফর্মুলা পর্যন্ত 2 টেবিলের খারাপ. আসুন কল্পনা করি $\alpha=\frac(1)(2)$ পর্যন্ত:

$$\left(u^(\frac(1)(2))\right)"=\frac(1)(2)\cdot u^(\frac(1)(2)-1)\cdot u" =\frac(1)(2)u^(-\frac(1)(2))\cdot u"\tag (4.2) $$

স্কিলকি $u^(\frac(1)(2))=\sqrt(u)$ i $u^(-\frac(1)(2))=\frac(1)(u^(\frac( 1) )(2)))=\frac(1)(\sqrt(u))$, তারপর সমতা (4.2) নিম্নরূপ পুনরায় লেখা যেতে পারে:

$$ (\sqrt(u))"=\frac(1)(2)\cdot \frac(1)(\sqrt(u))\cdot u"=\frac(1)(2\sqrt(u) )\cdot u" $$

অট্রিম্যানের সমতা $(sqrt(u))"=\frac(1)(2sqrt(u))cdot u"$ i є সূত্র নং 4 অনুরূপ টেবিলের। Bachite-এর মত, সারণীর সূত্র নং 3 এবং নং 4-এর সূত্র নং 2-এর অনুরূপ $alfa $ এর অনুরূপ মানের প্রতিস্থাপন সহ।