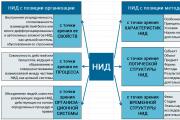
Lineárny omyl vektora sú nedostatkami riešenia. Lineárne ladené a lineárne nezávislé vektory
Vektory, їх sila a dії z nich
Vektory, dії z vektory, lineárny vektorový priestor.
Poradie konečných čísel je usporiadané podľa vektora.
Dії: 1. Násobenie vektora číslom: lambda * vektor x \u003d (lamda * x 1, lambda * x 2 ... lambda * x n). (3,4, 0, 7) * 3 \u003d (9, 12,0,21 )
2. Skladanie vektorov (aby ležali na rovnakom vektorovom priestore) vektor x + vektor y \u003d (x 1 + y 1, x 2 + y 2, ... x n + y n,)
3. Vektor 0=(0,0…0)---n E n – n-rozmerný (lineárny priestor) vektor x + vektor 0 = vektor x
Veta. Aby systém n vektorov, n-svetový lineárny priestor bol lineárne ladený, je potrebné a postačujúce, aby jeden z vektorov bol lineárnou kombináciou iných.
Veta. Be-yaka sukupnіst n+ 1. vektor n-svetová lineárna rozloha yavl. lineárny úhor.
Sčítanie vektorov, násobenie vektorov číslami. Vidnіmannya vektorіv.
Súčet dvoch vektorov sa nazýva vektor, ktorý sa narovnáva od klasu vektora po koniec vektora, aby sa zistilo, že klas je z konca vektora. Rovnako ako sú vektory nastavené ich rozložením podľa vektorov základnej jednotky, keď sú vektory zložené, ich príslušné súradnice sa pridajú.
Pozrime sa na príklad karteziánskeho súradnicového systému. Poď
Ukážme čo
Z baby 3 to vidíte ![]()

Súčet ľubovoľného koncového počtu vektorov možno nájsť za pravidlom bagatokutnika (obr. 4): na indukciu súčtu koncového počtu vektorov stačí zobrať ucho ofenzívneho vektora kože pomocou koniec predného vektora a indukujte vektor, ktorý ide za ucho prvého vektora s koncom zvyšku.

Sila operácie skladania vektorov:
V cich virase m, n su cisla.
Rozdiel vektorov sa nazýva vektor. Ďalším doplnkovým vektorom je vektor, protilový vektor za priamkou, ale rovný druhému.

Týmto spôsobom je operácia pohybu vektora nahradená operáciou skladania
Vektor, ktorého klas sa nachádza na klase súradníc, a koniec - v bode A (x1, y1, z1) sa nazýva polomerový vektor bodu A i alebo jednoducho. Úlomky jogových súradníc sú posunuté od súradníc bodu A, je možné vidieť rozloženie joga pozdĺž vektorov
Vektor, ktorý môže začínať v bode A(x1, y1, z1) a končiť v bode B(x2, y2, z2) ![]()
de r 2 - vektor polomeru bodu; r1 je vektor polomeru bodu A.
Preto je možné vidieť rozloženie vektora z hľadiska vektorov
Yogo dozhina je krajšia medzi bodmi A a B
VYNÁSOBIŤ
Takže v prípade plochých úloh je pridanie vektora na a = (ax; ay) k číslu b za vzorcom
a b = (ax b; ay b)
Príklad 1. Nájdite prírastok vektora a = (1; 2) o 3.
3a = (3 1; 3 2) = (3; 6)
Takže v prípade priestorového problému je za vzorcom zvýšenie vektora a = (ax; ay; az) o číslo b
a b = (ax b; ay b; az b)
Príklad 1. Nájdite prírastok vektora a = (1; 2; -5) o 2.
2a = (2 1; 2 2; 2 (-5)) = (2; 4; -10)
Skalárny dobootok vector_v that ![]() de - Strih medzi vektormi i; yakscho abo teda
de - Strih medzi vektormi i; yakscho abo teda
Z hľadiska skalárneho stvorenia kričíte, že ![]()
de, napríklad є hodnota premietania vektora priamo do vektora .
Skalárny štvorcový vektor:
Sila skalárneho stvorenia:
![]()
![]()
![]()
![]()
Skalárne otáčanie na súradniciach
Yakscho ![]()
![]() potom
potom ![]()
Kut mizh vektory
Rez medzi vektormi – strih medzi rovnými čiarami medzi vektormi (najmenší strih).
Vector TV (Vektorová TV dvoch vektorov) tse pseudovektor, kolmý na rovinu, pobudovanoї na dvoch spіvnásobičov, čo je výsledkom binárnej operácie "vektorové násobenie" nad vektormi v triviálnom euklidovskom priestore. Twіr nie je є ani komutatívny, ani asociatívny (je antikomutatívny) a funguje ako skalárny dobutku vektorіv. Pre bohatých inžinierov a fyziku je potrebné, aby matka mohla byť vektorom kolmým na dve reality - vektorová TV má byť možná. Vektorové predĺženie corisny pre „obrátenie“ kolmosti vektorov je dĺžka vektorového predĺženia dvoch vektorov v smere predĺženia ich dozhinov, keďže sú kolmé, a mení sa na nulu, keďže vektory sú rovnobežné, resp. antiparalelné.
Vektor tvir bol priradený iba trivimeru a siedmim svetovým šíram. Výsledok vytvorenia vektora, podobne ako skalárneho, leží v euklidovskej priestorovej metrike.
Z pohľadu vzorca na výpočet súradníc vektorového skalárneho objektu v trojrozmernom pravouhlom súradnicovom systéme, vzorec pre vektorový objekt leží v orientácii pravouhlého súradnicového systému, alebo inak "chiralita"
Kolinearizmus vektorov.
Dva nenulové (nerovnajúce sa 0) vektory sa nazývajú kolineárne, pretože ležia na rovnobežných priamkach alebo na tej istej priamke. Je prípustné, ale neodporúča sa ako synonymum - "paralelné" vektory. Kolineárne vektory môžu byť rovnako narovnané („smery“) alebo opačne narovnané (v ostatnom prípade sa niekedy nazývajú „antikolineárne“ alebo „antiparalelné“).
Zmіshane viroblennya vektorіv( a, b, c)- skalárne rozšírenie vektora a na vektorové rozšírenie vektora b a c:
(a, b, c) = a ⋅ (b × c)
niekedy sa tomu hovorí trinárne skalárne vytváranie vektorov, možno cez tie, ktorých výsledkom je skalár (presnejšie pseudoskalár).
Geometrický zmist: Modul kreatívy zmіsha je číselne dôležitejší ako povinnosť rovnobežnostenu vytvoreného vektormi (a, b, c) .
moc
Zmіshané tvir je šikmo symetrické vo vzťahu ku všetkým svojim argumentom: t.j. e) permutácia, či existujú dve spіvmulnikiv zmeny znamenia stvorenia. Výsledky ukazujú, že zmena okrem pravého karteziánskeho súradnicového systému (v ortonormálnej báze) je bližšie k maticovému vektoru poskladanému z vektora i:
Zmeny okrem ľavého karteziánskeho súradnicového systému (na ortonormálnom základe) sa rovnajú označeniu matice, poskladané z vektorov a prijaté so znamienkom „mínus“:
Zokrema,
Ako keby tam boli dva vektory a rovnobežné, tak s tretím vektorom smrad vytvorí zmätok, ktorý sa rovná nule.
Existujú tri vektory, ktoré sú lineárne ladené (to znamená, že sú koplanárne, ležia v rovnakej rovine) a ich odchýlky sú rovné nule.
Geometrický zmist - Zmіshane tvіr pre absolútnu hodnotu povinného paralepipeda (božských maličkých), tvoreného vektormi i; znamenie položiť zálohu v poriadku, chi є tsya triyka vektor_v vpravo chi leva.
Komplanarita vektorov.
Tri vektory (alebo viac) sa nazývajú koplanárne, ako keby zápach, redukovaný na klas, ležal v rovnakej rovine
Dominancia koplanarity
Ak chcete, aby jeden z troch vektorov bol nulový, potom tieto tri vektory môžu byť tiež koplanárne.
Trojica vektorov na pomstu páru kolineárnych vektorov, ktoré sú koplanárne.
Zmishane tvir koplanárne vektory. Ce je kritériom pre koplanaritu troch vektorov.
Sprievodné vektory - lineárne úhory. Tse je tiež kritériom koplanarity.
V priestore 3 svetov tvoria základ 3 nekoplanárne vektory
Lineárne ladené a lineárne nezávislé vektory.
Lineárne úhorové a nezávislé vektorové systémy.Vymenovanie. Vektorový systém je tzv lineárny úhor ak len jedna netriviálna lineárna kombinácia týchto vektorov, ktorá sa rovná nulovému vektoru. V každom prípade. len triviálna lineárna kombinácia týchto vektorov na nulový vektor, vektory sa nazývajú lineárne nezávislé.
Veta (kritérium lineárneho úhoru). Aby sústava vektorov v lineárnom priestore bola lineárne ladná, je potrebné a postačujúce, teda akceptovať jeden z týchto vektorov v lineárnej kombinácii iných.
1) Ak je stredný vektor, ak chcete jeden nulový vektor, potom je celý systém vektorov lineárne ladný.
Pravda, ako napríklad vvahayuchi, možno netriviálna lineárna kombinácia.
2) Akonáhle sú stredné vektory stanovené lineárne úhorom, potom je celý systém lineárne úhorom.
Dobre, nech sú to vektory, lineárne vklady. Je to tiež netriviálna lineárna kombinácia, ktorá je podobná nulovému vektoru. Ale todi, hádam ![]() berieme tiež netriviálnu lineárnu kombináciu rovnú nulovému vektoru.
berieme tiež netriviálnu lineárnu kombináciu rovnú nulovému vektoru.
2. Základ a rozmirnist. Vymenovanie. Systém lineárne nezávislých vektorov ![]() vektorový priestor sa nazýva základ tho priestor, ako keby vektor mohol byť reprezentovaný lineárnou kombináciou vektorov v systéme, tzn. pre kožný vektor
vektorový priestor sa nazýva základ tho priestor, ako keby vektor mohol byť reprezentovaný lineárnou kombináciou vektorov v systéme, tzn. pre kožný vektor ![]() tak, čo môže byť miestom žiarlivosti Tsya sa nazýva žiarlivosť vektorové rozloženie za základom a číslami
tak, čo môže byť miestom žiarlivosti Tsya sa nazýva žiarlivosť vektorové rozloženie za základom a číslami ![]() volal súradnice vektora podľa zákl(inak na základni) .
volal súradnice vektora podľa zákl(inak na základni) .
Veta (o jednote usporiadania za základňou). Koža vektora môže byť rozšírená nad rámec základne. jedna hodnosť, tobto. súradnice kožného vektora na zákl jasne vyniknúť.
Úloha 1. Systém vektorov Z'yasuvati, chi je lineárne nezávislý. Systém vektorov je daný maticou systému, ktorej stĺpce sú sčítané zo súradníc vektorov.
 .
.
Riešenie. Poď on line kombinácia  rovná sa nule. Po zaznamenaní rovnosti qiu v súradniciach vezmeme nasledujúci systém rovnováhy:
rovná sa nule. Po zaznamenaní rovnosti qiu v súradniciach vezmeme nasledujúci systém rovnováhy:
 .
.
Takýto systém rovných sa nazýva trikut. Existuje len jedno riešenie  . Otec, vektori
. Otec, vektori  lineárne nezávislé.
lineárne nezávislé.
Úloha 2. Z'yasuvati, chi є lineárne nezávislý systém vektorov.
 .
.
Riešenie. vektory  lineárne nezávislé (rozdiel. úloha 1). Povedzme, že vektor je lineárna kombinácia vektorov
lineárne nezávislé (rozdiel. úloha 1). Povedzme, že vektor je lineárna kombinácia vektorov  . Koeficienty rozloženia pre vektory
. Koeficienty rozloženia pre vektory  stiahnutý z vyrovnávacieho systému
stiahnutý z vyrovnávacieho systému
 .
.
Systém Tsya je zložitý, existuje len jedno riešenie.
Otec, systém vektorov  lineárne ladom.
lineárne ladom.
Rešpekt. Matice tohto druhu, podobne ako v úlohe 1, sa nazývajú zložité a úlohy 2 - často zložité . Výživa lineárneho úhoru sústavy vektorov sa dá ľahko pomýliť, podobne ako matica, poskladaná zo súradníc týchto vektorov, je často trojuholníková. Ak matica nemá špeciálny vzhľad, potom o pomoc elementárna transformácia riadkov , Scho zberіgayut lineárne spіvvіdnoshennia mіzh stovptsami, її môže byť znížená na podobne-zložitý vzhľad.
Elementárne transformácie riadkov matice (EPS) sa nazývajú ďalšie operácie na matici:
1) permutácia riadkov;
2) násobenie riadku na danom nulovom čísle;
3) pridanie do riadku nasledujúceho riadku, vynásobené určitým číslom.
Úloha 3. Nájdite maximálny lineárne nezávislý podsystém a vypočítajte hodnosť vektorového systému
 .
.
Riešenie. Nasmerujme maticu systému po pomoci NPS na podobný-často ošemetný vzhľad. Na vysvetlenie poradia dіy, riadok s číslom matice, ktorá sa transformuje, má význam symbolom . V zadnej časti stĺpca sú šípky zobrazené nad riadkami matice, pretože na odstránenie riadkov novej matice je potrebné viconovať.

 .
.
Je zrejmé, že prvé dva stĺpce vynechanej matice sú lineárne nezávislé, tretí stĺpec je rovnaká lineárna kombinácia a štvrtý stĺpec nie je možné uložiť do prvých dvoch. vektory  sa nazývajú základné. Zakladajú maximálny lineárne nezávislý subsystém systému
sa nazývajú základné. Zakladajú maximálny lineárne nezávislý subsystém systému  , A poradie systému je tri.
, A poradie systému je tri.
Základ, súradnice
Úloha 4. Nájdite základ a súradnice vektorov na ktorých základe na neosobných geometrických vektoroch, ktorých súradnice potešia myseľ  .
.
Riešenie. Bagato є ploché, scho prejsť klasom súradníc. Dodatočná báza v rovine je vytvorená z dvoch nekolineárnych vektorov. Súradnice vektorov vo vybranom základe sú určené systémom lineárnych zarovnaní rozvyazkoy vydpovidnoy.
Іsnuє th іnshіy sposіb vyvіshennya tsgogo zavdannya, ak môžete poznať základ pre súradnice.
Súradnice  otvorený priestor so súradnicami na byte
otvorený priestor so súradnicami na byte  ktorá nie je nezávislá. Nezávislé premenné i (nazývajú sa voľné) jednoznačne priraďujú vektor na ploche i, preto ich možno brať so súradnicami v . Rovnaký základ
ktorá nie je nezávislá. Nezávislé premenné i (nazývajú sa voľné) jednoznačne priraďujú vektor na ploche i, preto ich možno brať so súradnicami v . Rovnaký základ  pozostáva z vektorov, ktoré ležia v rôznych súboroch voľných zmien
pozostáva z vektorov, ktoré ležia v rôznych súboroch voľných zmien  і
і  , potom .
, potom .
Úloha 5. Poznať základ a súradnice vektorov pre každý základ na bohatých vektoroch v priestore, pre ktoré sú nepárové súradnice navzájom rovné.
Riešenie. Vibero, rovnako ako ja v úlohe vpred, koordinuje v priestore.
tak jaka  , potom sa zmeníš
, potom sa zmeníš  jednoznačne priraďte vektor i, potom súradnice є. Premenná báza je zložená z vektorov.
jednoznačne priraďte vektor i, potom súradnice є. Premenná báza je zložená z vektorov.
Úloha 6. Nájdite základ a súradnice vektorov, v ktorých základe na neosobných všetkých maticiach  , de
, de  - Poriadne číslo.
- Poriadne číslo.
Riešenie. Matrica kože h je jednoznačne znázornená v zobrazení:
Tse spіvіdnoshennia є razladannyam vektor z základ  so súradnicami
so súradnicami  .
.
Úloha 7. Nájdite expanziu a základ lineárnej obálky vektorového systému
 .
.
Riešenie. Prerobme maticu so súradnicami vektora v systéme za pomoci EPS na podobne ošemetný vzhľad.


 .
.
Stovptsi  zvyšné matice sú lineárne nezávislé a zvyšné matice
zvyšné matice sú lineárne nezávislé a zvyšné matice  lineárne vrazhayutsya krіz nich. Otec, vektori
lineárne vrazhayutsya krіz nich. Otec, vektori  vytvoriť základ
vytvoriť základ  , і
, і  .
.
Rešpekt. Základ y  zvolený nejednoznačne. Napríklad vektor
zvolený nejednoznačne. Napríklad vektor  tiež stanoviť základ
tiež stanoviť základ  .
.
Vektorový systém je tzv lineárny úhor, yakshcho іsnuyet takі čísla, medzi yakhocha by chcel byť jeden vіdminno vіd nula, scho vykonuєtsya vyrovnanosť. >.
Ako môže vyrovnanosť vyhrať iba v takom prípade, ak všetko, potom sa nazýva systém vektorov lineárne nezávislé.
Veta. Vektorový systém bude lineárny úhor vtedy a len vtedy, ak chcete jeden z її vektorov v lineárnej kombinácii iných.
príklad 1. Bohatý člen ![]() є lineárna kombinácia bohatých segmentov. Bohaté výrazy, aby sa stal lineárne nezávislým systémom, tak ako bohatý člen https: //pandia.ru/text/78/624/images/image012_44.gif" width="129" height="24">.
є lineárna kombinácia bohatých segmentov. Bohaté výrazy, aby sa stal lineárne nezávislým systémom, tak ako bohatý člen https: //pandia.ru/text/78/624/images/image012_44.gif" width="129" height="24">.
zadok 2. Maticový systém, https://pandia.ru/text/78/624/images/image016_37.gif" width="51" .ru/text/78/624/images/image019_27.gif" width="69" height= "21"> /images/image022_26.gif" width="40" lineárny úhor.
Riešenie.
Ukladáme lineárnu kombináciu týchto vektorov https://pandia.ru/text/78/624/images/image023_29.gif" 22">.
Vzhľadom na rovnaké súradnice rovnakých vektorov vezmeme width="289" height="69">
Reziduálny
 і
і
Systém môže mať jedno triviálne riešenie, takže lineárna kombinácia týchto vektorov dosiahne nulu viackrát, ak všetky koeficienty dosiahnu nulu. Tom daný systém vektor_v lineárne nezávislý.
zadok 4. Vektory sú lineárne nezávislé. Aké budú systémy vektorov
a).![]() ;
;
b).![]() ?
?
Riešenie.
a). Pridáme lineárnu kombináciu a prirovnáme ju k nule
Vykoristovuyuchi silu operácií s vektormi v lineárnom priestore, prepíšeme zostávajúcu ekvivalenciu vizuálneho
Keďže vektory sú lineárne nezávislé, potom sa koeficienty viny musia rovnať nule, takže gif.
Otrimanov systém je rovnocenný, existuje len jedno triviálne riešenie ![]() .
.
Oskіlki rivnіst (*) vykonuєtsya iba pri - lineárne nezávislé;
b). Ukladanie rovnosti https://pandia.ru/text/78/624/images/image039_17.gif" (**)
Zastosovuyuchi analogický mirkuvannya, otrimaєmo
Virishyuchi systém vyrovnania Gausovou metódou, je to nevyhnutné
 alebo
alebo
Zvyšok systému je neosobné riešenie https://pandia.ru/text/78/624/images/image044_14.gif" width="149" height="24 src=">. žiarlivosť víťazí (**)
. Otec, systém vektorov ![]() - Lineárny úhor.
- Lineárny úhor.
zadok 5 Vektorový systém je lineárne nezávislý a vektorový systém je lineárne nezávislý. gif. (***)
Pri žiarlivosti (***) . V skutočnosti bol systém lineárne ladený.
Zі spіvіdnoshennia (***)
prijateľné ![]() alebo
alebo ![]() Výrazne
Výrazne ![]() .
.
Zobrať ![]()
Úloha pre nezávislé riešenie(v publiku)
1. Systém, ktorý pomstí nulový vektor, je lineárne ladený.
2. Systém, ktorý pozostáva z jedného vektora a, lineárne úhor rovnomerne a menej ako, ak, a=0.
3. Systém, ktorý sa skladá z dvoch vektorov, je lineárne ladený iba vtedy, ak sú vektory proporcionálne (teda jeden z nich vychádza z najmenšieho násobenia číslom).
4. Ak k lineárnemu systému úhoru pridáte vektor, uvidíte systém lineárneho úhoru.
5. Ako z lineárne nezávislého systému, vektor je vidieť, systém vektorov je lineárne nezávislý.
6. systém Yakscho S lineárne nezávislý, ale pri pridávaní vektora lineárne klesá b, potom vektor b lineárne sa ohýba cez vektory systému S.
c). Systém matíc má iné poradie matíc.
10. Nech je sústava vektorov a,b,c vektorový priestor je lineárne nezávislý. Priniesť lineárnu nezávislosť útočných vektorových systémov:
a).a+b, b, c.
b).a+https://pandia.ru/text/78/624/images/image062_13.gif" width="15" height="19">– dostatočný počet
c).a+b, a+c, b+c.
11. Poď a,b,c- tri vektory na byte, medzi nimi môžete zložiť tricutnik. vektory čchi čchi budú lineárne klesať?
12. Dané dva vektory a1=(1, 2, 3, 4),a2=(0, 0, 0, 1). Vyberte ďalšie dva chotirivimir vektory a3 aa4 takze, shob system a1,a2,a3,a4 bula lineárne nezávislé .
Vymenovanie. Lineárna kombinácia vektorov a 1, ..., a n
x 1 a 1 + ... + x n a n.
triviálne takže všetky koeficienty x 1 , ..., x n sú rovné nule.
Vymenovanie. Lineárna kombinácia x 1 a 1 + ... + x n a n sa nazýva netriviálne, aj keď jeden z koeficientov x 1, ..., x n sa nerovná nule.
lineárne nezávislé, takže neexistuje žiadna netriviálna kombinácia týchto vektorov rovnajúca sa nulovému vektoru .
Takže vektory a 1 ..., a n sú lineárne nezávislé ako x 1 a 1 + ... + x n a n = 0 párne a iba ak x 1 = 0, ..., x n = 0.
Vymenovanie. Nazývajú sa vektory a 1 , ..., a n lineárny úhor yakscho іsnuє netriviálna kombinácia tsikh vector_v do_vnyuє nulový vektor.
Dominancia lineárnych úhorových vektorov:
Pre n-té vektory.
n + 1 vektor lineárnych usadenín.
Pre 2 a 3 svetové vektory.
Dva riadky úhorový vektor- kolineárny. (Kolіnearnі vektory - lineárne vklady.) .
Pre tri pokojné vektory.
Tri lineárne úhorové vektory - koplanárne. (Tri koplanárne vektory - lineárne vklady.)
Aplikujte úlohu na lineárnu nezávislosť a lineárnu nezávislosť vektorov:
Príklad 1. Obrátenie vektora a = (3; 4; 5), b = (-3; 0; 5), c = (4; 4; 4), d = (3; 4; 0) sú lineárne nezávislé.
Riešenie:
Vektory budú lineárne ladené, škálovacie vektory budú menšie pre počet vektorov.
Príklad 2. Obrátenie vektora a = (1; 1; 1), b = (1; 2; 0), c = (0; -1; 1) sú lineárne nezávislé.
Riešenie:
| x1 + x2 = 0 | |
| x1 + 2x2 - x3 = 0 | |
| x1 + x3 = 0 |
| 1 | 1 | 0 | 0 | ~ | ||
| 1 | 2 | -1 | 0 | |||
| 1 | 0 | 1 | 0 |
| ~ | 1 | 1 | 0 | 0 | ~ | 1 | 1 | 0 | 0 | ~ | ||||
| 1 - 1 | 2 - 1 | -1 - 0 | 0 - 0 | 0 | 1 | -1 | 0 | |||||||
| 1 - 1 | 0 - 1 | 1 - 0 | 0 - 0 | 0 | -1 | 1 | 0 |
z prvého radu je vidieť ďalší; do tretieho radu dodamo dalsie:
| ~ | 1 - 0 | 1 - 1 | 0 - (-1) | 0 - 0 | ~ | 1 | 0 | 1 | 0 | ||||
| 0 | 1 | -1 | 0 | 0 | 1 | -1 | 0 | ||||||
| 0 + 0 | -1 + 1 | 1 + (-1) | 0 + 0 | 0 | 0 | 0 | 0 |
Toto riešenie ukazuje, že systém dokáže vytvoriť neosobné riešenie tak, že má nenulovú kombináciu hodnôt čísel x 1 x 2 x 3 takú, že lineárna kombinácia vektorov a, b, c sa rovná nulový vektor, napríklad:
A + b + c = 0
a tse znamená, že vektory a, b, c sú lineárne uloženia.
Návrh: vektory a, b, c sú lineárne ladené.
Príklad 3. Obrátenie vektora a = (1; 1; 1), b = (1; 2; 0), c = (0; -1; 2) sú lineárne nezávislé.
Riešenie: Poznáme hodnotu koeficientov pre ľubovoľnú lineárnu kombináciu týchto vektorov v nulovom vektore.
x 1 a + x 2 b + x 3 c 1 = 0Zarovnanie vektorov Tse možno zaznamenať vo vizuálnom systéme lineárnych zarovnaní
| x1 + x2 = 0 | |
| x1 + 2x2 - x3 = 0 | |
| x1 + 2x3 = 0 |
Vikoristický systém kontrolujeme Gaussovou metódou
| 1 | 1 | 0 | 0 | ~ | ||
| 1 | 2 | -1 | 0 | |||
| 1 | 0 | 2 | 0 |
z iného radu je vidieť prvý; z tretieho riadku vidíme prvý:
| ~ | 1 | 1 | 0 | 0 | ~ | 1 | 1 | 0 | 0 | ~ | ||||
| 1 - 1 | 2 - 1 | -1 - 0 | 0 - 0 | 0 | 1 | -1 | 0 | |||||||
| 1 - 1 | 0 - 1 | 2 - 0 | 0 - 0 | 0 | -1 | 2 | 0 |
z prvého radu je vidieť ďalší; až do tretieho radu dodamo ďalší.
Lineárny úhor lineárna nezávislosť vektor_v.
Vektorové základy. Aténsky súradnicový systém
V posluchárni je veľa čokolád a pár sladkého drievka sa dnes bude môcť dostať z kože - analytická geometria s lineárnou algebrou. Tento článok bude rozdelený na dve časti pokročilá matematika, a sme zvedaví, ako si smradi zvyknú na jeden kopček. Dajte si pauzu, s'zh "Tviks"! ... baby, no super dievčatko. Ak chcem, nedám gól, prepáčte, viem sa na tréning naladiť pozitívne.
Lineárny úhor vektorov, lineárna nezávislosť vektorov, vektorový základ tento pojem nemusí byť len geometrický výklad, ale predovšetkým algebraický význam. Samotný pojem „vektor“ z pohľadu lineárnej algebry nie je ani zďaleka rovnaký ako „nadradený“ vektor, ktorý môžeme reprezentovať v rovine priestoru. Pre dôkaz netreba chodiť ďaleko, skúste namaľovať vektor päťrozmerného priestoru. ![]() . Abo len počkajte, pre niektorých som išiel do Gіsmeteo: - teplota a atmosférický tlak sú dobré. Pažba samozrejme nie je správna z hľadiska autority vektorového priestoru, ale nič nebráni formalizácii údajov parametrami a vektorom. Dych jesene.
. Abo len počkajte, pre niektorých som išiel do Gіsmeteo: - teplota a atmosférický tlak sú dobré. Pažba samozrejme nie je správna z hľadiska autority vektorového priestoru, ale nič nebráni formalizácii údajov parametrami a vektorom. Dych jesene.
Ahoj, nebudem ťa pokúšať teóriou, lineárne vektorové priestory, problém je v tom rozumieť definícia tejto vety. Nové pojmy (lineárny vklad, nezávislosť, lineárna kombinácia, báza atď.) sú z hľadiska algebry prídavné mená ku všetkým vektorom, ale uplatnenie bude dané geometricky. V tomto rangu je všetko jednoduché, dostupné na prvý pohľad. Analytická geometria Krіm zavdan je považovaná za typickú úlohu algebry. Na zvládnutie materiálu je potrebné naučiť sa lekcie Vektory pre čajníkyі Ako počítať?
Lineárny úhor a nezávislosť vektora v rovine.
Plošný základ a afinitný súradnicový systém
Pozrime sa na vašu oblasť počítačový stôl(len stolík, nočné stolíky, polienka do postele, stély, kto potrebuje). Líder poľa v najbližších dňoch:
1) Vyberte základ oblasti. Zhruba kazhuchi, stіlnitsa maє dovzhina і šírka, intuitívne si uvedomil, že na stimuláciu základu sú potrebné dva vektory. Jeden vektor zjavne nestačí, tri vektory sú zayva.
2) Na základe obrátenej báze nastaviť súradnicový systém(súradnicová mriežka) na priradenie súradníc všetkým objektom, ktoré sú na stole.
Nečudujte sa, vysvetlenie bude na prstoch. A na tvojom. Buďte láskaví, odpúšťajte výrazný prst ľavej ruky na okraj slohu tak, že som sa čudoval monitoru. Tse bude vektor. Teraz miesto malíček pravej ruky na kraji stola len tak - schob buv rovnanie na obrazovke monitora. Tse bude vektor. Usmej sa, vyzeráš úžasne! Čo môžete povedať o vektoroch? Dátové vektory kolineárne, čo znamená lineárne otočiť jeden cez jeden:
, no, chi navpaki: , de - deake číslo, vіdmіnne vіd nula.
Obrázok toho, ktorú akciu si možno pozrieť v lekcii Vektory pre čajníky De I vysvetlil pravidlo násobenia vektora číslom.
Či vaše prsty nastavia základ na počítačovom stole? Očividne nie. Kolіnearnі vektory a rast cien tu a tam sám priamo vpred a oblasť môže byť dlhšia a širšia.
Takéto vektory sa nazývajú lineárny úhor.
záver: Slová „lineárny“, „lineárny“ znamenajú veci, ktoré sa matematicky rovná, neexistujú žiadne štvorce, kocky, iné kroky, logaritmy, sínusy. Є tіlki linіynі (1. etapa) proti úhoru.
Dve vektorové roviny lineárne vklady vtedy a len vtedy, ak je zápach kolineárny.
Prekrížte prsty na stole, aby ste medzi nimi boli ako rez Krymu 0 alebo 180 stupňov. Dve vektorové rovinylineárne nie zatuchnutý v tom a menej, pretože smrad nie je kolineárny. Otzhe, základ je odobratý. Nemusíte sa báť, že základ pohľadov je „kosený“ nekolmými vektormi rôznych dĺžok. Nie je pre mňa nezvyčajné, že pre jogu nie je prívesok iba 90 stupňov, a nie iba jeden, rovný starému vektoru.
Be-jaky plochý vektor jedna hodnosť rozšírené podľa základu: ![]() , de - dіysnі čísla. Volať čísla vektorové súradnice na akom základe.
, de - dіysnі čísla. Volať čísla vektorové súradnice na akom základe.
Zdá sa teda vektorvýkony na pohľad lineárna kombinácia bázové vektory. Tobto viraz sa volá vektorové rozloženiezáklad alebo lineárna kombinácia základné vektory.
Napríklad možno povedať, že vektor rozložení je za ortonormálnym základom roviny, alebo možno povedať, že znázornenia lineárnej kombinácie vektorov sú nesprávne.
Formulovať priradenie k základu formálne: Základ oblasti nazýva sa dvojica lineárne nezávislých (nekolineárnych) vektorov, , na ktorom byť ako Rovinný vektor je lineárna kombinácia základných vektorov.
Samotným momentom vymenovania je skutočnosť, že vektory sú brané v poradí skladieb. Basisi ![]() - existujú dve absolútne odlišné základne! Ako sa zdá, malíček ľavej ruky nemožno presunúť na malíček pravej ruky.
- existujú dve absolútne odlišné základne! Ako sa zdá, malíček ľavej ruky nemožno presunúť na malíček pravej ruky.
Základ máme vypracovaný, ale stále nestačí nastaviť súradnicovú mriežku a priradiť súradnice skin objektu vašej počítačovej tabuľky. Prečo si zmeškal? Vektory є vіlnimi a rozmazané cez celú rovinu. Ako teda priradíte súradnice k týmto malým putovným bodom na stole, ktoré zostali po bujarom víkende? Požadované usmernenie. І takýto orientačný bod je známy každému - klas súradníc. Vyberá sa zo súradnicového systému:
Začnem „školskými“ organizáciami. Už na úvodnej hodine Vektory pre čajníky Videl som skutky uznania medzi pravouhlým súradnicovým systémom a ortonormálnym základom. Štandardný obrázok osi:

Keď sa hovorí o pravouhlý súradnicový systém, potom najbežnejším spôsobom je použitie klasu súradníc, súradnicovej osi a mierky pozdĺž osí. Skúste do vyhľadávacieho systému zadať „obdĺžnikový súradnicový systém“ a poviete mi, že stojí za to povedať vám o znalostiach 5. – 6. triedy súradnicovej osi a o tom, ako umiestniť body do roviny.
Na druhej strane existuje efekt, že pravouhlý súradnicový systém možno definovať ako celok prostredníctvom ortonormálneho základu. І tse mayzhe tak. Vzorec znie takto:
klas súradníc, і ortonormalizácia nastaviť základ Kartézsky pravouhlý súradnicový systém roviny . Ide o pravouhlý súradnicový systém určite sú reprezentované jedným bodom a dvoma jednoduchými ortogonálnymi vektormi. Práve z tohto dôvodu potrebujete stoličku, ako som vám vštepil višche - in geometrické problémyčasto (aj keď nie zavzhd) maľuje і vektory, і súradnicové osi.
Myslím, že každý pochopil, že pre ďalší bod (klas súradníc), ktorý je ortonormálny k základni BE-YAKIY BODY oblasti a BE-YAKIYA VEKTOR oblasti môžete priradiť súradnice. Obrazne povedané, „na námestí sa dá očíslovať všetko“.
Môžu byť súradnicové vektory jednoduché? Nі, smrad môže matka dovіlnu nenulová dovzhina. Pozrime sa na bod a dva ortogonálne vektory a pomerne nenulové hodnoty:

Takýto základ je tzv ortogonálne. Klas súradníc s vektormi nastavuje súradnicovú mriežku a či už ide o bod roviny, či už ide o vektor, ktorý zapíše súradnice do tohto základu. Napríklad, alebo. Zjavná nešikovnosť spočíva v tom, že súradnicové vektory na vrchole kopca smútiť za rôznymi životmi, vіdminnі vіd odinitsі. Akonáhle sa osamelosť vyrovná, potom vychádza primárny ortonormálny základ.
! Poznámka : v ortogonálnej základni a tiež nižšie v aténskych základniach sa berú do úvahy roviny a priestor jednej pozdĺž osí UMOVIMI. Napríklad v jednej jednotke pozdĺž osi x sú 4 cm, v jednej jednotke pozdĺž osi 2 cm.
A ďalšie jedlo, na jaka, je to naozaj daný dôkaz - čo obov'yazykovo kut medzi základnými vektormi môže dosiahnuť 90 stupňov? Ahoj! Ako potvrdiť schôdzku, základné vektory a poplatky menej ako nekolineárne. Vidpovidno kut mozhe buti be-yakim, krіm 0 a 180 stupňov.
Bod roviny, ako sa tomu hovorí klas súradníc, і nekolineárne vektory, , sada afinný súradnicový systém roviny :

Inými slovami, takýto súradnicový systém sa nazýva opletené systém. Ako aplikovať body a vektory na obrázok kresla: 
Ako viete, aténsky súradnicový systém je menej jednoduchý, nepoužívajú vzorce pre vektory a vdrіzkiv, ako sme sa pozreli na druhú časť lekcie Vektory pre čajníky, bohato pikantné formulky, pov'yazanі z skalárne vytváranie vektorov. Ďalej sú tu spravodlivé pravidlá pre skladanie vektora a násobenie vektora číslom, vzorce na delenie na daný výraz a tiež pre deakovanie typov úloh, na ktoré sa môžeme ľahko pozrieť.
A visnovok je taký, že je to najpohodlnejší spôsob, ako nazvať bod aténskeho súradnicového systému - karteziánsky pravouhlý systém. K tomu її, radšej, najčastejšie a byť privedený k bachiti. ... Medzitým je všetko v tomto živote jasné - je len málo situácií, v ktorých je samotná rieka skreslená (inak napr. polárny) súradnicový systém. Títo humanoidi si takéto systémy môžu užívať =)
Prejdime k praktickej časti. Usі zavdannya táto lekcia je rovnako ako pravouhlý súradnicový systém, takže zagalnogo aténskej vpadku. Nie je tu nič skladateľné, všetok materiál je prístupný školákovi.
Ako definovať kolinearitu vektora v rovine?
Typická rieka. Aby sme mali dva vektory a oblasti ![]() byť kolineárne, nevyhnutné a dostatočné, aby ich vhodné súradnice boli proporcionálne. V skutočnosti ide o súradnicové detaily zrejmého spivvіdnoshenya.
byť kolineárne, nevyhnutné a dostatočné, aby ich vhodné súradnice boli proporcionálne. V skutočnosti ide o súradnicové detaily zrejmého spivvіdnoshenya.
zadok 1
a) Reverzné, chi kolineárne vektory ![]() .
.
b) Chi stanovte základ vektora ![]() ?
?
Riešenie:
a) Prečo, čo platí pre vektory ![]() koeficient proporcionality tak, že zvíťazili rovnosti:
koeficient proporcionality tak, že zvíťazili rovnosti: ![]()
Obov'yazkovo rozpovіm o "pіzhonskiy" variant zastosuvannya tsgogo pravidiel, ktorý je v obehu v praxi. Myšlienka spočíva v tom, že okamžite spočítate pomer a budete vedieť, či budete mať pravdu:
Pridajme podiel daných súradníc vektorov:
čoskoro:
, v tomto poradí sú zodpovedajúce súradnice proporcionálne,
Nastavenie je možné zložiť a zložiť, cenná možnosť:
Pre sebaoverenie môžete použiť tie, ktoré sú kolineárnymi vektormi, a lineárne ohýbať jeden cez druhý. Z tohto hľadiska existuje miesto rovnocennosti ![]() . Vaša spravodlivosť je ľahko perveryaetsya prostredníctvom elementárnych divízií s vektormi:
. Vaša spravodlivosť je ľahko perveryaetsya prostredníctvom elementárnych divízií s vektormi: 
b) Dva vektory a roviny vytvárajú základ, ako keby boli kolineárne (lineárne nezávislé). Doslіdzhuєmo na kolіnearnіst vektori ![]() . Poďme zostaviť systém:
. Poďme zostaviť systém: 
Od prvého rovnakého kričíš, scho, od druhého rovného, kričíš, oh, systém je šialený(Neexistuje žiadne riešenie). Týmto spôsobom zodpovedajúce súradnice vektorov nie sú proporcionálne.
Višňovok: vektory sú lineárne nezávislé a tvoria základ.
Zjednodušená verzia riešenia vyzerá takto:
Sčítame podiel daných súradníc vektorov ![]() :
:
, Otzhe, qi vektory a lineárne nezávislé a vytvoriť základ.
Zavolaním tejto možnosti odmietnete recenzentov, ale obviňujete problém za zlyhania, ak sú súradnice rovné nule. os takto: ![]() . Abo takto:
. Abo takto: ![]() . Abo takto:
. Abo takto: ![]() . Ako tu môžem pracovať prostredníctvom pomeru? (Naozaj sa nedá deliť nulou). Z rovnakého dôvodu som jednoduchšie riešenie nazval „pizhonsky“.
. Ako tu môžem pracovať prostredníctvom pomeru? (Naozaj sa nedá deliť nulou). Z rovnakého dôvodu som jednoduchšie riešenie nazval „pizhonsky“.
Návrh: a), b) schváliť.
Malý kreatívny príklad pre nezávislú víziu:
zadok 2
Pre ľubovoľnú hodnotu parametra vektor ![]() bude kolineárny?
bude kolineárny?
Pre riešenie sa parameter nájde prostredníctvom pomeru.
Pre kolineárnosť využívame metódu algebry opätovného overovania vektorov.
Pre dva vektory v oblasti ekvivalentnej tvrdosti:
2) vektory a vytvorenie základu;
3) vektory nie sú kolineárne;
+ 5) oscilátor, záhyby zo súradníc týchto vektorov, vіdminny vіd nula.
Vidpovidno, ekvivalentná protraktilná tvrdosť chodidla:
1) vektorové a lineárne vklady;
2) vektory nespĺňajú základ;
3) vektory a kolineáre;
4) vektory môžu byť lineárne obrátené jeden za druhým;
+ 5) vektor, skladanie zo súradníc týchto vektorov, čo vedie k nule.
Už som o tom presvedčený daný moment už ste pochopili všetky pojmy, ktoré ste sa naučili, a potvrdili ste to.
Pozrime sa na novú správu, piaty odsek: dva vektory a plochy ![]() kolіnearnі thodі і tіlki tіlki tоdі, ak vyznachnik, poskladá sa zo súradníc týchto vector_v, do_vnyuє nula:. Pre zastosuvannya tsієї znamenia, prirodzene, je potrebné pamätať poznať vizionárov.
kolіnearnі thodі і tіlki tіlki tоdі, ak vyznachnik, poskladá sa zo súradníc týchto vector_v, do_vnyuє nula:. Pre zastosuvannya tsієї znamenia, prirodzene, je potrebné pamätať poznať vizionárov.
Virišima Príklad 1 iným spôsobom:
a) Výpočet počtu vektorov, sčítanie súradníc vektorov ![]() :
:![]() , tiež q vektorov a kolineár.
, tiež q vektorov a kolineár.
b) Dva vektory a roviny vytvárajú základ, ako keby boli kolineárne (lineárne nezávislé). Výpočet počtu vektorov, skladanie súradníc vektorov ![]() :
:![]() , Otzhe, vektory sú lineárne nezávislé a vytvárajú základ.
, Otzhe, vektory sú lineárne nezávislé a vytvárajú základ.
Návrh: a), b) schváliť.
Vyzerá výrazne kompaktnejšie a krajšie, nižšie riešenie s proporciami.
Pomocou skúmaného materiálu je možné stanoviť kolineárnosť vektorov a tiež priniesť rovnobežnosť vdrіzkіv, priamych čiar. Poďme sa pozrieť na pár úloh z konkrétnych geometrických tvarov.
zadok 3
Vzhľadom na vrcholy chotirikutnik. Prineste, že chotirikutnik je rovnobežník.
Prinášanie: Kreslo v úlohe nebude potrebné, čriepky riešenia budú čisto analytické
rovnobežník
nazýva sa chotirikutnik, ktorý má protiľahlé strany v pároch rovnobežné.
V tomto poradí je potrebné priniesť:
1) rovnobežnosť protiľahlých strán;
2) rovnobežnosť protiľahlých strán.
Prinášame:
1) Poznáme vektory: 
![]()
2) Poznáme vektory: 
Viyshov je rovnaký vektor („podľa školy“ - rovnaké vektory). Kolіnearnіst je už zrejmé, ale je lepšie usporiadať riešenie správne, s usporiadaním. Vypočítajme počet vektorov zložením súradníc vektorov: ![]() , Otzhe, qі vektory a kolinearnі, t.j.
, Otzhe, qі vektory a kolinearnі, t.j.
Višňovok: Protilezhnі strany chotirikutnik v pároch paralelne, otzhe, vіn є rovnobežník pre schôdzky. Čo bolo potrebné priniesť.
Ďalšie postavy dobrých:
zadok 4
Vzhľadom na vrcholy chotirikutnik. Priniesť, scho chotirikutnik є trapezієyu.
Pre suvorish vzorec dokážte krajšie, skvostne, nakreslite označenie lichobežníka a len ho doplňte a len hádajte, akoby ste sa pozerali von.
Tse zavdannya nezávislé riešenie. Vonkajšie riešenie ako lekcia.
A teraz nastal čas pomaly prejsť z bytu do otvoreného priestoru:
Ako určiť kolinearitu vektora v priestore?
Pravidlo je podobné. Aby boli dva vektory v priestore kolineárne, je potrebné a postačujúce, aby ich príslušné súradnice boli proporcionálne.
zadok 5
Z'yasuvati, chi kolіnearnі budú posúvať vektory a priestor:
a);
b)
v) ![]()
Riešenie:
a) Reverzibilne, chi je koeficient úmernosti pre rôzne súradnice vektorov:
Systém nie je možné rozlíšiť, preto vektory nie sú kolineárne.
"Sproschenka" sa robí opätovným pomerom. V tomto pohľade:
– relatívne súradnice nie sú proporcionálne, takže vektory nie sú kolineárne.
Návrh: vektory nie sú kolineárne.
b-c) Toto sú body nezávislého rozhodnutia. Skúste jogu ozdobiť dvoma spôsobmi.
Použite metódu opätovného overenia priestorových vektorov pre kolinearitu prostredníctvom premennej tretieho rádu, táto metóda je uvedená v článku Vektor TV vektor.
Podobne ako pri plošnom pohľade na nástroje môže stagnovať spôsob zachovania rovnobežnosti otvorených priestorov a priamok.
Prosíme vás o ďalšie oddelenie:
Lineárna zatuchnutosť a nezávislosť sú vektormi v trivimerovom priestore.
Priestranný základ a afinitný súradnicový systém
Množstvo zákonov, ako sme videli na námestí, bude spravodlivých a priestranných. Synopsu teórie som sa snažil minimalizovať, kúsky ľavej časti informácií sú už rozlúštené. Tim nie je o nič menej, odporúčam prečítať si úvodnú časť s rešpektom, čriepky sú nové pojmy a rozumieť.
Teraz sa výmena plochy počítačového stola rozširuje na trojrozmerný priestor. Vytvorme základ jogy. Kto vie, kto je v dome, kto je na ulici, ale v každom prípade nemôžeme ísť nikam v troch svetoch: šírka, dĺžka a výška. Preto sú na vyvolanie základu potrebné tri priestorové vektory. Jeden alebo dva vektory nestačia, štvrtiny sú zayvi.
Som opäť rozminaєmos na prstoch. Buďte láskaví, zdvihnite ruku do kopca a zdvihnite pupienok na rôznych stranách skvelé, pôsobivé prostredník . Tse budú vektory, smrad bude žasnúť na rôznych stranách, smútiť rôzne dozhiny a smútiť medzi sebou rôzne kuti. Vіtayu, základ trivimirovej rozlohy je pripravený! Pred rečou nie je potrebné predvádzať také vikladachy, ako nekrútiť prstami, ale nikam nemôžete ísť =)
Dajme dôležité jedlo, byť ako tri vektory a uspokojiť základ trivi-svetského priestoru? Buďte láskaví a pevne stlačte tri prsty na stôl počítača. Čo sa stalo? Tri vektory sa pohybovali v tej istej rovine a zhruba sa zdá, že máme jeden znak vimirivu - výšku. Takéto vektory koplanárny A je celkom zrejmé, že základ trivimerického priestoru nemožno vytvoriť.
Treba poznamenať, že koplanárne vektory a nič zlého ležia v rovnakej rovine, môžu byť v rovnobežných rovinách (skúste pracovať iba prstami, takže Salvador Dali by sa namotal menej =)).
Vymenovanie: vektory sú pomenované koplanárny ako skutočný byt, ako paralelný smrad. Tu je logické dodať, že ak takáto oblasť neexistuje, vektory nebudú koplanárne.
Tri koplanárne vektory a lineárne uloženia tobto lineárne vrazhayutsya jeden cez jeden. Pre jednoduchosť je opäť prijateľné, že smrad leží v jednom byte. Po prvé, vektory, a nielen to, sú koplanárne, môžu byť viac kolineárne, aj keď vektor možno vidieť cez vektor. Iným spôsobom, napríklad, vektory nie sú kolineárne, potom sa cez ne tretí vektor otáča v jedinom poradí: ![]() (a prečo je ľahké uhádnuť pre materiály predchádzajúcej divízie).
(a prečo je ľahké uhádnuť pre materiály predchádzajúcej divízie).
Spravodlivý je návrat tvrdenia: tri nekoplanárne vektory a lineárne nezávislé vektory, tobto už n_yak nie vrazhayutsya jeden cez jeden. Ja, samozrejme, som menej ako takéto vektory a môžem uspokojiť základ triviálneho rozsahu.
Vymenovanie: Základ trivimirnogo rozloha nazývaná trojica lineárne nezávislých (nekoplanárnych) vektorov, prevzaté zo speváckeho poriadku kedykoľvek, nech je to vektor otvoreného priestoru jedna hodnosť rozložené na danej báze, súradnice vektora na danej báze
Hádajte, môžete tiež povedať, že vektor reprezentácií lineárna kombinácia základné vektory.
Koncepcia súradnicového systému je zavedená rovnakým spôsobom, ako pre plochý svah stačí jeden bod a tri lineárne nezávislé vektory:
klas súradníc, і nekoplanárne vektory, prevzaté zo speváckeho poriadku, sada affinnu sústava súradníc priestoru trivi-sveta
:
Je zrejmé, že súradnicová mriežka „vrkoča“ nie je príliš efektívna, ale vyzvaný súradnicový systém nám umožňuje určite označte súradnice ľubovoľného vektora, ktoré súradnice akéhokoľvek bodu v priestore. Podobne ako v rovine, v aténskom súradnicovom systéme priestor nepracuje podľa rovnakých vzorcov, o ktorých som už hádal.
Najprimárnejší a najpohodlnejší termín pre afinitný súradnicový systém є pravouhlý súradnicový systém:
Ukážte do priestoru, ako sa tomu hovorí klas súradníc, і ortonormalizácia nastaviť základ Kartézsky pravouhlý súradnicový systém
. Poznať obrázok: 
Predtým, ako prejsť k praktickým úlohám, znova systematizujem informácie:
Pre tri vektory v priestore ekvivalentné rovnakej tuhosti:
1) vektory sú lineárne nezávislé;
2) vektory a vytvorenie základu;
3) vektory nie sú koplanárne;
4) vektory nemožno lineárne obracať jeden po druhom;
5) vyznachnik, skladanie súradníc týchto vektorov, vіdminny vіd nula.
Protilezhnі vyslovlyuvannya, hádať, zrozumіlі.
Lineárny pád/nezávislosť vektora v priestore sa tradične posudzuje za pomoci menovaného (odsek 5). Tі, scho stratené praktické úlohy nesú jasné vyjadrenie algebraického charakteru. Je čas zavesiť geometrický kľúč na kvety a ovládať baseballovú pálku lineárnej algebry:
Tri vektorové priestory complanarnі thodі і tіlki tіlki tіlі, ak vyznachnik, zložené súradnice danih vektor_v, do_vnyuє zero :  .
.
Venujem pozornosť malej technickej nuancii: súradnice vektorov sa dajú zaznamenať nielen v stĺpci, ale aj v riadku (hodnota vektora sa nemení - sila vektorov je úžasná). Ale bohatší je krajší na stovptsі, oskіlki tse vigіdnіshe pre splnenie niektorých praktických úloh.
Tim čitateľom, ktorí zabudli na metódy rozrahunky maturantov, alebo sa v nich možno slabo orientujú, odporúčam jednu z mojich najstarších lekcií: Ako počítať?
zadok 6
Overte si, či nasledujúce vektory tvoria základ triviálnej rozlohy:
Riešenie: V skutočnosti sa všetky rozhodnutia robia podľa výpočtu dlžníka
a) Vypočítajte premennú poskladaním zo súradníc vektora_v (premenná expanzie pozdĺž prvého riadku): 
, Otzhe, vektory sú lineárne nezávislé (nie koplanárne) a tvoria základ triviálneho priestoru.
Vidpovid: dané vektory a uspokojiť základ
b) Toto je bod nezávislého rozhodnutia. Navonok je riešením to, že je to podobné ako pri lekcii.
Crawl a kreatívni pracovníci:
zadok 7
Pre akú hodnotu parametra budú vektory koplanárne?
Riešenie: Vektory a koplanárne todі tіlki tіlki dі, ak vyznachnik, záhyby súradníc týchto vektorov na nulu: 
V skutočnosti je potrebné rovnať sa vyznachnikovi. Je to naliate na nuly ako šuliky na jerboas - čo znamená, že navigátor zistí v inom rade a v rade, budem hľadať mínusy: 
Vykonajte ďalšie predĺženie a otočte ho sprava na najjednoduchšie lineárne zarovnanie: ![]()
Vidpovid: o
Tu je ľahké zosúladiť, pre ktoré je potrebné podložiť hodnotu bývalej úradníčky a prehodnotiť  , otvorenie jogy nanovo.
, otvorenie jogy nanovo.
Na záver sa pozrieme ešte na jednu typické úlohy, ktorý má viac algebraický charakter a je tradične súčasťou kurzu lineárnej algebry. Podlaha je rozšírená, čo si zaslúži veľkú dosku:
Aby sme priniesli, že 3 vektory vytvárajú základ priestoru trivi-sveta
a poznať súradnice 4. vektora v danom základe
zadok 8
Daný vektor. Ukážte, že vektory vyhovujú základu trivimerového priestoru a poznáte súradnice vektora, na ktorom základe.
Riešenie: Na zátylku zachytávame myseľ Pre myseľ má dané chotiri vektory a podobne ako Bachite je zápach už mayutových súradníc na rovnakom základe. Čo je základ - nedráždi nás. A povedať takú vec: tri vektory ako celok môžu vytvoriť nový základ. Prvá etapa opäť vychádza z riešení z Prílohy 6, je potrebné skontrolovať, či sú vektory skutočne lineárne nezávislé:
Vypočítajme počet vektorov zložením súradníc vektorov: 
, Otzhe, vektory sú lineárne nezávislé a vytvárajú základ trivi-svetového priestoru.
! dôležité : vektorové súradnice obov'azkovo zapisovateľné na stanici vyznachnika, nie v radoch. V opačnom prípade dôjde k podvodu v ďalších algoritmoch rozvyazannya.