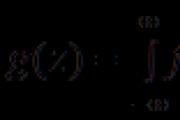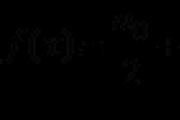Pravidlá a vzorce diferenciácie sú podobné skladacím funkciám. Funkcia skladania

Funkcie skladací vzhľad nie je správne nazývať ju pojmom „skladacia funkcia“. Napríklad, vyzerajúci ešte viac zmierený, ale funkcia skladania nie je, na vіdmіnu vіd.

Pri tsіy statti mi porozumieme skladacia funkcia, učíme sa ukazovať її v skladoch elementárnych funkcií, dávame vzorec na známosť її podobného a reportovateľného riešenia charakteristických aplikácií.

V prípade dokonalých aplikácií neustále víťazíme v tabuľke podobných a pravidiel diferenciácie, preto ich pred vašimi očami orezávajte.

skladacia funkcia- Toto je funkcia, ktorej argument je tiež funkciou.

Podľa nášho názoru je účel najrozumnejší. Chytro môžete myslieť f(g(x)). To znamená, že g(x) ako argument funkcie f(g(x)) .

Napríklad nech f je funkcia arkustangens a g(x) = lnx je funkcia prirodzeného logaritmu, takže skladacia funkcia f(g(x)) je funkciou arctg(lnx). Ďalší zadok: f je funkcia prepojenia so štvrtým krokom a - tsila racionálna funkcia (čuduj sa), todi .

Svojím spôsobom môže byť g(x) skladacou funkciou. Napríklad, . Šikovne sa takýto viráž pozná ako . Tu je f funkcia sínusu, funkcia variácie odmocniny, - Racionálna funkcia brokovnice. Je logické priznať, že kroky investovania funkcií môžu byť ako finále prirodzené číslo.

Často stačí zavolať funkciu zloženie funkcií.

Vzorec známej funkcie skladania.

zadok.

Spoznajte praktické funkcie skladania.

Riešenie.

V tomto prípade f je štvorcová funkcia a g(x) = 2x+1 je lineárna funkcia.

Osou zostavy je riešenie s rôznymi vzorcami pre podobnú funkciu skladania:

Poďme vedieť, čo budem robiť, keď som sa vopred opýtal na externé funkcie.

Otzhe,

Rovnako ako bachite, výsledky zbіgayutsya.

Snažte sa nezablúdiť ako funkcia є f , ale ako g(x) .

Vysvetlime to pažbou pre rešpekt.

zadok.

Poznajte praktické funkcie skladania, ktoré .

Riešenie.

V prvom prípade je f funkcia štvorca a g(x) je funkcia sínus, takže
.

Z iného pohľadu je f sínusová funkcia a a je stavová funkcia. Neskôr môžu byť pre vzorec ďalšie funkcie skladania

Je možné vidieť vzorec podobnej funkcie

zadok.

Diferencujte funkciu .

Riešenie.

Pre ktorú funkciu skladania zadku si môžete v duchu napísať ako , defunkcia sínusu, funkcia väzby na tretí krok, funkcia logaritmu na báze e, funkcia odberu arkustangens a lineárna funkcia druhého kroku.

Za vzorcom podobnej funkcie skladania

Teraz už vieme

Spoločne vyberieme odpočítané medzivýsledky:

Nie je nič strašné, vytriedte si skladacie funkcie ako matrioshka.

Na ktorom z nich môžem dokončiť článok, yakby zhodne ale ...

Bazhano jasne rozumie, ak nastavíte pravidlá diferenciácie a tabuľku podobných, a ak vzorec podobnej funkcie skladania.

PROSÍM, BUĎTE OBZVLÁŠŤ REŠPEKTOVANÝ. Povedzme si niečo o zavádzaní funkcií v súvislosti so skladacími funkciami. Navyše si ušetríte sily, a ak budete mať šťastie, budete úspešní.

Učme sa z jednoduchých aplikácií. funkciu môžete vidieť, ako to skladám: g(x) = tgx , . Tiež môžete okamžite zastosovuvat vzorec pokhіdnoї skladacia funkcia

Funkcia osi nemožno nazvať skladací.

Táto funkcia je súčtom troch funkcií 3tgx i 1 . Hocha - є skladacia funkcia: - statická funkcia (kvadratická parabola) a f - tangentová funkcia. Na tento účel vložíme vzorec na diferenciáciu sumi:

Stratil som znalosti o nasledujúcich skladacích funkciách:

Tom.

Spodіvaєmosya, scho ste zachytili podstatu.

Aby ste boli ešte úžasnejší, môžete sa uistiť, že skladacie funkcie môžu byť zahrnuté v sklade skladacích funkcií a skladacie funkcie môžu byť úložnými časťami skladacích funkcií.

Ako je vytriedený zadok pre úložné časti funkcie .

Perche Toto je skladacia funkcia, ako si viete predstaviť, kde f je logaritmická funkcia na základe 3 a g(x) je súčet dvoch funkcií і . Tobto, .

Iným spôsobom, Venujme sa funkcii h (x). Vyhrané .

Súčet dvoch funkcií je , de - Skladacia funkcia s číselným koeficientom 3 . - funkcia prepojenia na kocku; - kosínusová funkcia; - lineárna funkcia.

Tse súčet dvoch funkcií i , de - skladacia funkcia, - exponenciálna funkcia, - statická funkcia.

Takýmto spôsobom

tretí, priechodný do , yak celá tá racionálna funkcia

Funkcia kvadratúry, - funkcia logaritmu na základe e.

Otec, .

Navrhované:

p align="justify"> Teraz je štruktúra funkcie pochopená a je jasné, ako sa vzorce a v postupnosti zastosovuvat pri її diferenciácii.

Pri rôznych funkciách diferenciácie (znakov budúcnosti) sa môžete poučiť z rozdielov podobných úloh.

Po predsunutej delostreleckej príprave budú menej desivé pažby s 3-4-5 prílohami funkcií. Je možné, že ak šliapnete dva zadky, budú ako skladacie, ale ak im rozumiete (či už trpíte), tak všetko ostatné v diferenciálnom výpočte môže mať detskú horúčku.

zadok 2

Poznať súvisiace funkcie

Ako to bolo zamýšľané, s potrebnou funkciou skladania zmeníme, je to potrebné správny ROZIBRATISYA pri vložkách. V tichých situáciách, ak pochybujete, uhádnem správny trik: vezmite si napríklad poslednú hodnotu „iks“ a skúste (mysliac v čiernej farbe) dať význam do „strašného vírusu“.

1) Potrebujeme spočítať viráz na zadnej strane, potom je suma najväčšia investícia.

2) Potom je potrebné vypočítať logaritmus:

4) Pridajme do kocky kosínus:

5) Na piatej najkratšej cene:

6) І, nareshti, samotná skutočná funkcia je druhá odmocnina:

Vzorec na diferenciáciu skladacej funkcie zastosovyvaetsya v opačnom poradí, vo forme najdôležitejšej funkcie, k vnútornej. Vidíme:

Chebto bez pardonu:

1) Pozrite sa na druhú odmocninu.

2) Postarajte sa o maloobchodné, zástupné pravidlo

3) Pokhіdna trojčatá sú drahšie na nulu. Pri ďalšom dodanovi urobíme krok (kocku).

4) Poďme sa pozrieť na kosínus.

6) Ja, nareshti, sa pozriem na najväčší vklad.

Možno je to dôležitejšie, ale stále to nie je najlepší zvierací zadok. Vezmite si napríklad výber Kuznetsova a oceníte všetku krásu a jednoduchosť zvoleného vzhľadu. Spomenul som si, že rád dám niečo na spánok, prehodnotím, aký je študent inteligentný, ako poznáte funkcie skladania, čo nie je múdre.

Urážlivý príklad nezávislého riešenia.

zadok 3

Poznať súvisiace funkcie

Pomôcka: Pravidlo linearity a pravidlo diferenciácie k stvoreniu sú postavené chrbtom k sebe

Navonok je riešením to, že je to podobné ako pri lekcii.

Prišla hodina prejsť na niečo kompaktnejšie a krajšie.
Nie je to zriedkavá situácia, keďže zadok nemá dve, ale tri funkcie. Ako spoznáte, či je práca troch multiplikátorov dobrá?

zadok 4

Poznať súvisiace funkcie

Trochu sa čudujeme, ale prečo sa tri funkcie nedajú previesť na dve funkcie? Napríklad yakby sme mali dve bohaté členitosti, potom bolo možné otvárať oblúky. Ale v aplikácii sú všetky funkcie rôznych: kroky, exponent a logaritmus.

V takýchto situáciách je to nevyhnutné postupne zastaviť pravidlo diferenciácie stvorenia dvakrát

Dôraz je kladený na skutočnosť, že pre "y" máme výrazne odlišné dve funkcie: a pre "ve" - ​​logaritmus: . Prečo dokážeš byť taký nepríjemný? Hiba - prečo nie dva násobky a pravidlo nefunguje? Nie je tam nič skladateľné:

Teraz zrazu stratil pravidlo pokloniť sa:

Stále sa môžete hnevať a obviňovať sa za chrámy, ale v tejto situácii je lepšie stratiť sa v takom pohľade - je ľahšie sa prevrátiť.

Nazretý zadok možno zlomiť aj iným spôsobom:

Urážlivé spôsoby ukončenia sú úplne rovnaké.

zadok 5

Poznať súvisiace funkcie

Toto je príklad nezávislého riešenia v prvom rade prvým spôsobom.

Pozrime sa na analogické aplikácie so zlomkami.

zadok 6

Poznať súvisiace funkcie

Tu môžete ísť niekoľkými spôsobmi:

Abo takto:

Riešením je však zapisovať kompaktnejšie, ako v prvom riadku, aby sa prekonalo pravidlo diferenciácie súkromných , Akceptujem celé číslo:

V princípe je zadok zlomený a ak sa pri takomto pohľade pripravíte o jogu, neminie vás. Ale, aby to bolo zrejmé, na hodinu to sfarbite do čierneho, ale prečo to nemôžete povedať?

Prinesme čísla do spiaceho transparentu a získajme trojitú plochu záberu:

Mínusom doplňujúcich otázok je fakt, že omilostenia môžu prísť nie v čase známych, ale banálnych premien školy. Na druhej strane, vikladachi často odmietajú úlohu a žiadajú, aby ju „priviedol do cesty“ horšiemu.

Najjednoduchší príklad nezávislej vízie:

zadok 7

Poznať súvisiace funkcie

Pokračujeme v ovládaní známosti známeho a hneď sa môžeme pozrieť na typickú odchýlku, ak sa „hrozný“ logaritmus šíri na rozlíšenie.

Operácia vizualizácie sa nazýva diferenciácia.

V dôsledku vývoja problémov o rozdiele medzi najjednoduchšími (a nie najjednoduchšími) funkciami označenia najhorších, ako aj medzi zdokonalením argumentácie, sa objavila tabuľka podobných a presne definovaných pravidiel diferenciácie. Isaac Newton (1643-1727) a Gottfried Wilhelm Leibniz (1646-1716) boli prví v oblasti poznania minulosti.

Preto v našej hodine, aby sme vedeli, či existujú nejaké funkcie, nie je potrebné počítať rozdiel medzi zlepšením funkcie a zlepšením argumentu, ale je potrebné urýchliť tabuľku podobných s pravidlá diferenciácie. Pre poznanie budúcnosti by sa mal použiť útočný algoritmus.

Poznať pokhidnu, povinny viraz pod znakom zdvihu rozšíriť sklad jednoduché funkcie ta vznachiti, yakami (tvir, sum, private) súvisiace s týmito funkciami. Dalі pokhіdnі elementárne funktsіy znachimo іv tabuľkáchі іn pokhіdnih, a vzorce pokhіdnih creativ, sum ta chasto - іv pravidlách diferenciácie. Tabuľka podobných pravidiel na rozlíšenie údajov po prvých dvoch aplikáciách.

príklad 1. Poznať súvisiace funkcie

Riešenie. Z pravidiel diferenciácie je zrejmé, že súčet funkcií je rovnaký ako súčet podobných funkcií, tj.

Z tabuliek podobných je zrejmé, že „iksa“ je to isté ako single a sínus je kosínus. Nahraďte hodnoty qi súčtom pokhіdnyh a poznáme nevyhnutnú mentálnu úlohu pokhіdnu:

zadok 2. Poznať súvisiace funkcie

Riešenie. Inak, ako keby som prišiel o svoju sumu, v nejakom inom dodatku s konštantným násobiteľom, môžem to viniť za znamenie zlého:

Pokiaľ je jedlo obviňované, berú sa hviezdy, zápach sa spravidla vyjasňuje po oboznámení sa s tabuľkou podobných a najjednoduchších pravidiel diferenciácie. Pred nimi naraz prejdeme.

Tabuľka podobných jednoduchých funkcií

1. Pokhіdna konštanty (čísla). Či už existuje číslo (1, 2, 5, 200 ...), takáto funkcia bude iná. Držte sa na nule. Je dôležitejšie pamätať na to, čo je častejšie potrebné
2. Pokhіdna nezalezhnaya zminnoy. Väčšinou „iksa“. Zabudnite na zdravú samotu. Je dôležité, aby ste si to dlho zapamätali
3. Pokhіdna krok. Na nohách čerešňovej hodiny je potrebné prerobiť neštvorcové korene.
4. Pokhіdna zminnoї v kroku -1
5. Pokhіdna odmocnina
6. Pokhіdna sinus
7. Pokhіdna kosínus
8. Pokhіdna dotyčnica
9. Pokhіdna kotangens
10. Podobne ako arcsínus
11. Podobne ako arkozín
12. Pokhіdna arctangens
13. Pokhіdna oblúková tangens
14. Podobné ako prirodzený logaritmus
15. Hrubá logaritmická funkcia
16. Pokhіdna exponenti
17. Funkcie zobrazenia Pokhidna

Pravidlá diferenciácie

1. Pokhіdna sumi chi maloobchod
2. Robte dobrú prácu
2a. Pokhіdna virazi, násobená konštantným multiplikátorom
3. Choďte do súkromia
4. Funkcia skladania

Pravidlo 1Aké funkcie

diferenciácia v aktuálnom bode, potom v rovnakom bode diferenciácie a funkcie

prečo

tobto. podobný súčet algebraických funkcií je podobný súčet algebier podobných funkcií.

Dôsledok. Ako dve funkcie, ktoré sa odlišujú, obnovujú pri stálom sčítaní, sú si potom podobné, potom.

Pravidlo 2Aké funkcie

diferencované v aktuálnom bode, potom v tom istom bode sú tieto dodatočné body diferencované

prečo

tobto. práca dvoch funkcií je dobrá pre súčet kožných prác s týmito funkciami pre zvyšok.

Posledná 1. Za zlé znamenie môže neustály multiplikátor:

Posledné 2. Pokhіdna vytvoriť dekilkoh funktsіy, scho differentenziyuyutsya, dobrіvnyuє tvorіvі vіdnoї kohіdnoї derzhnoi z spіvmnіnіkіv іn all іnshі.

Napríklad pre tri násobky:

Pravidlo 3Aké funkcie

diferenciácie v bode deyakіy і , potom sa v tomto bode diferencuje a iu/v navyše

tobto. podobne ako pri súkromnom dvojfunkčnom zábere, číslovka takého rozdielu výtvorov bannermana pre mŕtveho numeralistu a numeralistu pre bannermana a bannermana je štvorec veľkej číslice.

De sho shukati na iných stranách

Keď viete dobré veci, robte to často u skutočných manažérov, je potrebné zastosovuvaty veľa pravidiel diferenciácie, takže existuje viac aplikácií na dobré časy - v štatistikách"Vytvorte si vlastné súkromné ​​funkcie".

Rešpekt.Šmyknite, aby ste nezamieňali konštantu (to číslo) ako súčet k súčtu a ako konštantný násobiteľ! Pre vipadiana je dodanka її pokhіdna drahšia na nulu a na čas rýchleho multiplikátora bude obviňovaná zo znamenia pokhіdnyh. Toto je typický pardon, ako sa to vidí v minulosti v štádiu šľachtenia klasov, ale vo svete sa už vidí, koľko jedno-dvojposchodových zásob stredný študent tsyu pardon už nerob.

A čo sa týka odlíšenia tvorby súkromného, ​​máte dodatok u"v, v ktorom u- číslo, napríklad 2 alebo 5, to je konštanta, potom sa rovnaké číslo bude rovnať nule i, potom sa všetky sčítania budú rovnať nule (taký vzorec argumentov v zadku 10).

Insha časté odpustenie- mechanické riešenie funkcie príležitostného skladania ako príležitostná jednoduchá funkcia. Tom skladacie funkcie venovaný okrem štatútu. Ale, chrbtom k sebe, viem lepšie jednoduché funkcie.

Po ceste sa nezaobídete bez zmeny virázy. Pre koho možno budete potrebovať pomoc z nových okien Dії zі kroky a koreneі Dії so zlomkami .

Ako nájdete riešenia podobných zlomkov s krokmi a odmocninami, takže ak sa funkcia môže pozrieť na , potom postupujte podľa lekcie "Je dobré mať vrece brokov s krokmi a koreňmi."

Yakshcho dobre pred vami zavdannya nachebto , potom ste zaneprázdnení "Vyrobnі jednoduchými goniometrickými funkciami".

Pokrokovi zadky - ako vedieť, či idem

príklad 3. Poznať súvisiace funkcie

Riešenie. Je zrejmé, že časť funkcie virázy: celý viráz predstavuje tvir, podobne ako multiplikátory - sumi, druhý má jeden multiplikátor navyše. Existuje pevné pravidlo diferenciácie pre tvorbu: vytvorte dve funkcie krajšie, súčet výtvorov kože a tieto funkcie pre zvyšok:

Dali sme stabilné pravidlo diferenciácie súčtu: súčet algebraických funkcií je podobný súčtu algebry podobných funkcií. Naša myseľ v kožnom vaku má ďalší dodatok so znamienkom mínus. V súčte pokožky je veľa nezávislých zmien, je to ako zdravé a konštanta (číslo), ktorá je ako nula. Otzhe, "iks" s nami transformuje do jedného, ​​a mínus 5 - na nulu. V inom prípade sa "iks" vynásobí 2, takže dva sa vynásobia tým istým, ako je "iks" preč. Odoberáme nasledujúce hodnoty:

Predstavme si, že súčet kreatív našiel nevyhnutné potreby mysle pre všetky funkcie:

A je možné zvrátiť vývoj úloh do budúcnosti.

zadok 4. Poznať súvisiace funkcie

Riešenie. Je potrebné, aby sme poznali tajomstvo súkromného. Zastosovuєmo vzorec diferentiyuvannya chastki: pokhіdna chastki dvoh funktsіy dorіvnyuє zlomok, počet takého rozdielu výtvorov zástavy pre smrť číslice a číslice pre smrť bannera, a banner je druhou mocninou čísla bannera číslovka. Berieme:

Vedeli sme už v zadku 2. Nezabúdajme, že je pravda, že ďalší sp_multiplier v číselnej knihe v zadku streamovania je braný so znamienkom mínus:

Ako sa pozeráte na všestrannosť takýchto úloh, pri ktorých potrebujete poznať presné funkcie, de sucile hromadenie koreňov tých krokov, ako napr. , potom láskavo požiadajte o prácu "Zábery Virobna sumi s krokmi a koreňmi" .

No, musíte vedieť viac o horších sínusoch, kosínusoch, tangenciách a iných goniometrické funkcie, potom, ak sa funkcia môže pozrieť na , potom máte lekciu "Úplné jednoduché goniometrické funkcie" .

Príklad 5. Poznať súvisiace funkcie

Riešenie. Táto funkcia má bachimo tver, jeden z ich spoločných násobiteľov je druhá odmocnina nezávislej zmeny, pričom podobnú sme poznali z tabuliek podobných. Za pravidlom diferenciácie sa vytvára táto tabuľková hodnota podobnej druhej odmocniny:

K riešeniu úloh do budúcnosti je možné sa vrátiť na online kalkulačky .

Príklad 6. Poznať súvisiace funkcie

Riešenie. Táto funkcia je viac súkromná, vzdialenosť ktorejkoľvek je druhou odmocninou nezávislej zmeny. Za pravidlom diferenciácie súkromného, ​​ako sme ho zopakovali a vložili do aplikácie 4, sa berie tabuľková hodnota podobnej druhej odmocniny:

Aby sme získali zlomok v číselníku, vynásobíme číselník a banner číslom.

Funkcie skladania vyzerajú ako bežné funkcie pre určenú funkciu skladania. Ak ide o funkciu tvaru y \u003d sin x - (2 - 3) a r c t g x x 5 7 x 10 - 17 x 3 + x - 11, potom її nemožno zložiť do zobrazenia y \u003d sin 2 x.

Tento článok ukáže pochopenie funkcie skladania a prejavu. Oprava so vzorcami významu podobného z zadkov riešenia do visnovky. Zastosuvannya tabuľky horšie a pravidlá diferenciácie výrazne zmeniť hodinu na zmenu horšie.

Hlavné stretnutia

Menovanie 1

Skladacia funkcia zvažuje takúto funkciu, rovnako ako argument je tiež funkciou.

Označuje sa takto: f (g (x)) . Je možné, že funkcia g(x) je zohľadnená argumentom f(g(x)).

Menovanie 2

Podobne funkcia f a є funkcia kotangens, potom g(x) = ln x je funkcia prirodzeného logaritmu. Všimnite si, že skladaciu funkciu f(g(x)) možno zapísať ako arctg(lnx). V opačnom prípade sa funkcia f, ktorá je funkciou 4 krokov, de g (x) \u003d x 2 + 2 x - 3 berie do úvahy celá racionálna funkcia, predpokladá sa, že f (g (x)) \ u003d (x 2 + 2 x - 3) 4 .

Je zrejmé, že g(x) môže byť zložiteľné. Zo zadku y \u003d sin 2 x + 1 x 3 - 5 je zrejmé, že hodnota g môže kubický koreň so zlomkom. Dánsky viraz možno označiť ako y \u003d f (f 1 (f 2 (x))). Hviezdy môžu znamenať, že f je funkcia sínusu a f 1 je funkcia, ktorá sa rozširuje pod druhú odmocninu, f 2 (x) \u003d 2 x + 1 x 3 - 5 je zlomková racionálna funkcia.

Menovanie 3

Sadzba príspevku je priradená ako nejaké prirodzené číslo a zapíše sa ako y = f (f 1 (f 2 (f 3 (... (f n (x))))))))).

Menovanie 4

Pochopenie zloženia funkcie spočíva v počte vstupných funkcií pre mentálnu úlohu. Pre dokonalosť víťazstva, vzorec pre podobnosť skladacej funkcie mysle

(f(g(x))) "=f"(g(x)) g"(x)

Použiť

zadok 1

Nájdite funkciu skladania tvaru y = (2 x + 1) 2 .

Riešenie

Je zrejmé, že f je štvorcová funkcia a g (x) \u003d 2 x + 1 sa berie do úvahy pri lineárnej funkcii.

Urobme podobný vzorec pre funkciu skladania a zapíšme si ho:

f"(g(x)) = ((g(x)) 2)" = 2 (g(x))2-1 = 2 g(x) = 2 (2x + 1); g "(x) = (2 x + 1)" = (2 x) "+ 1" = 2 x " + 0 = 2 1 x 1 - 1 = 2 ⇒ (f (g (x))) "=f "(g(x)) g"(x) = 2 (2x + 1) 2 = 8x + 4

Je potrebné vedieť, ako zjednodušiť funkciu vonkajšieho vzhľadu. Berieme:

y = (2x + 1) 2 = 4x2 + 4x + 1

Zvіdsi maєmo, scho

y"=(4x2+4x+1)"=(4x2)"+(4x)"+1"=4(x2)"+4(x)"+0==4 2 x 2 - 1 + 4 1 x 1 - 1 = 8 x + 4

Výsledky boli skreslené.

Pri vykonávaní úlohy tohto druhu je dôležité pochopiť, de-roztashovuvatimovať funkciu tvaru f і g (x) .

zadok 2

Mali by ste poznať nasledujúce funkcie skladania tvaru y \u003d sin 2 x a y \u003d sin x 2.

Riešenie

Prvým záznamom funkcie je, aby sa zhodovalo s tým, že f je funkcia štvorca a g (x) je funkcia sínus. Todi otrimaemo to

y "= (sin 2 x)" = 2 sin 2 - 1 x (sin x)" = 2 sin x cos x

Iný zápis ukazuje, že f je sínusová funkcia a g(x) = x 2 je zmysluplné štátna funkcia. Znie to tak, že dodatočná skladacia funkcia bude napísaná ako

y " \u003d (sin x 2) " \u003d cos (x 2) (x 2) " \u003d cos (x 2) 2 x 2 - 1 \u003d 2 x cos (x 2)

Vzorec pre náhodné y \u003d f (f 1 (f 2 (f 3 (... (fn (x)))))))) je napísaný ako y "= f" (f 1 (f 2 (f 3 (. . . .) fn (x))))) f 1 "(f 2 (f 3 (... (fn (x))))) f 2 " (f 3 (... (fn (x))))). . . f n "(x)

zadok 3

Nájdite podobnú funkciu y = sin (ln 3 a r c t g (2 x)).

Riešenie

Dánsky zadok zobrazuje skladanie záznamu a označenie rozšírenia funkcií. Potom y \u003d f (f 1 (f 2 (f 3 (f 4 (x))))) je významné, de f , f 1 , f 2 , f 3 , f 4 (x) 3 kroky, funkcia s logaritmom a základom e, funkciou arkustangens a lineárnej.

3 vzorce na označenie skladacej funkcie

y "= f "(f 1 (f 2 (f 3 (f 4 (x))))) f 1 "(f 2 (f 3 (f 4 (x))))) f 2 "( f 3 ( f 4 (x))) f 3 "(f 4 (x)) f 4 "(x)

Berieme to, čo potrebujeme vedieť

1. f "(f 1 (f 2 (f 3 (f 4 (x))))) = cos (ln 3 arctg (2x)).
2. f 1 "(f 2 (f 3 (f 4 (x)))) (2 x) = 3 ln 2 arctg (2 x) .
3. f 2 "(f 3 (f 4 (x))) je podobne logaritmické, potom f 2 "(f 3 (f 4 (x))) = 1 a r c t g (2 x) .
4. f 3 "(f 4 (x)) ako podobný oblúkový tangens, potom f 3 "(f 4 (x)) \u003d 1 1 + (2 x) 2 \u003d 1 1 + 4 x 2.
5. Pri významnom f 4 (x) \u003d 2 x existuje vina 2 pre znamienko podobnej statickej funkcie s exponentom, ktorý je dobrý 1 potom f 4 "(x) \u003d (2 x)" \u003d 2 x "= 2 1 x 1 - 1 = 2.

Vykonávame súhrn priebežných výsledkov a berieme to do úvahy

y "= f "(f 1 (f 2 (f 3 (f 4 (x))))) f 1 "(f 2 (f 3 (f 4 (x))))) f 2 "( f 3 ( f 4 (x))) f 3 "(f 4 (x)) f 4 "(x) = = cos (ln 3 arctan (2 x)) 3 ln 2 arctan (2 x) 1 arctan (2 x) 1 1 + 4 x 2 2 = = 6 cos (ln 3 arktan (2 x)) ln 2 arktan (2 x) arktan (2 x) (1 + 4 x 2 )

Analýza takýchto funkcií vytvorí matrioshky. Pravidlá diferenciácie nie je možné vždy zafixovať zrejmé za pomoc tabuliek horšieho. Najčastejšie je potrebné zapísať vzorec pre význam podobných skladacích funkcií.

Іsnuyut deyakі vіdminnostі skladací typ skladacích funkcií. S jasným pochopením rozdielov je obzvlášť ľahké rozpoznať tie neskoršie.

zadok 4

Treba sa pozrieť na mierenie takéhoto zadku. Ak je to funkcia tvaru y \u003d tg 2 x + 3 tgx + 1, potom to možno považovať za skladací tvar g (x) \u003d tgx, f (g) \u003d g 2 + 3 g + 1 . Je zrejmé, že je potrebné zostaviť vzorce pre skladací vzorec:

f "(g (x)) = (g 2 (x) + 3 g (x) + 1)" = (g 2 (x)) "+ (3 g (x))" + 1 " == 2 g 2 - 1 (x) + 3 g "(x) + 0 \u003d 2 g (x) + 3 1 g 1 - 1 (x) \u003d \u003d 2 g (x) + 3 \u003d 2 tgx + 3; g " (x) = (tgx) " = 1 cos 2 x ⇒ y " = (f (g (x))) " = f " (g (x)) g" (x) = (2 tgx + 3 ) 1 cos 2 x = 2 tanx + 3 cos 2 x

Funkcia v tvare y = t g x 2 + 3 t g x + 1 sa nepovažuje za skladaciu; Avšak t g x 2 sa považuje za skladaciu funkciu, potom statická funkcia tvaru g (x) = x 2 і f je tangensová funkcia. Pre koho by sa mala odlíšiť taška. Akceptujeme to

y " = (tgx 2 + 3 tgx + 1) " = (tgx 2) " + (3 tgx) " + 1 " == (tgx 2) " + 3 (tgx) " + 0 = (tgx 2) " + 3 čo 2 x

Poďme k hodnote podobnej funkcie skladania (t g x 2) ":

f "(g (x)) \u003d (tg (g (x)))" \u003d 1 cos 2 g (x) \u003d 1 cos 2 (x 2) g "(x) \u003d (x 2)" \u003d 2 x 2 - 1 \u003d 2 x ⇒ (tgx 2) "= f "(g (x)) g "(x) \u003d 2 x cos 2 (x 2)

Berieme, že y "= (t g x 2 + 3 t g x + 1)" = (t g x 2) "+ 3 cos 2 x = 2 x cos 2 (x 2) + 3 cos 2 x

Skladacie funkcie môžu byť zahrnuté pred skladacími funkciami a samotné skladacie funkcie môžu byť skladové skladacie funkcie.

zadok 5

Pozrime sa napríklad na skladateľnú funkciu tvaru y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x (x 2 + 1)

Táto funkcia môže byť vyjadrená ako y = f (g (x)), kde hodnota f je funkciou logaritmu na základe 3 a g (x) sa berie ako súčet dvoch funkcií tvaru h ( x) = x 2 + 3 cos 3 (2 x + 1) + 7 ex 2 + 3 3 i k(x) = ln 2 x (x 2 + 1) . Je zrejmé, že y = f(h(x) + k(x)) .

Pozrime sa na funkciu h(x) . Cena l (x) \u003d x 2 + 3 cos 3 (2 x + 1) + 7 až m (x) \u003d e x 2 + 3 3

Možno l(x) \u003d x 2 + 3 cos 2 (2 x + 1) + 7 \u003d n (x) + p (x) - súčet dvoch funkcií n (x) \u003d x 2 + 7 a p (x) \u003d 3 cos 3 (2 x + 1), de p (x) \u003d 3 p 1 (p 2 (p 3 (x))) je skladacia funkcia s číselným koeficientom 3 a p 1 je a funkcia kocky, funkcia p 2 kosínus, p 3 (x) = 2 x + 1 - lineárna funkcia.

Vzali sme, že m (x) = ex 2 + 3 3 = q (x) + r (x) - súčet dvoch funkcií q (x) = ex 2 і r (x) = 3 3 de q (x) = q 1 (q 2 (x)) je skladacia funkcia, q 1 je funkcia s exponentom, q 2 (x) = x 2 je stavová funkcia.

Je možné vidieť, že h (x) = l (x) m (x) = n (x) + p (x) q (x) + r (x) = n (x) + 3 p 1 (p 2 ( p 3 (x))) q 1 (q 2 (x)) + r (x)

Pri prechode na zobrazenie tvaru k(x) = ln 2 x (x 2 + 1) = s (x) t (x) je zrejmé, že funkcia je prezentovaná vo forme skladania s(x) = ln 2 x = s 1 ( s 2 (x)) s racionálnym číslom t (x) \u003d x 2 + 1, de s 1 є kvadratická funkcia a s 2 (x) \u003d ln x - logaritmické so základom e .

Vyzerá to tak, že uvidím k (x) = s (x) t (x) = s 1 (s 2 (x)) t (x) .

Todi otrimaemo to

y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 ex 2 + 3 3 + ln 2 x (x 2 + 1) = = fn (x) + 3 p 1 (p 2 (p 3 ( x))) q 1 (q 2 (x)) = r (x) + s 1 (s 2 (x)) t (x)

Za štruktúrami funkcie sa ukázalo, ako a ako je potrebné upevniť vzorce, aby sa zjednodušil výraz na diferenciáciu. Aby sme takéto úlohy poznali a porozumeli im, je potrebné vrátiť sa k bodu diferenciácie funkcie, aby bolo dôležité im porozumieť.

Akoby ste si spomenuli na pardon v texte, buďte láskaví, pozrite si to a stlačte Ctrl + Enter

Prvá veta o skladacej funkcii, ktorá je formulovaná takto:

Poďme 1) funkcia $u=\varphi (x)$ môže mať $u_(x)"=\varphi"(x_0)$ v prvom bode $x_0$; 2) funkcia $y=f(u)$ sa môže zmeniť $y_(u)"=f"(u)$ pre najnovšie body $u_0=\varphi (x_0)$. Podobne je aj skladacia funkcia $y=f\left(\varphi (x) \right)$ v bode hádania podobná, rovná sa dodatočnému spracovaniu podobných funkcií $f(u)$ a $\varphi (x) $:

$$ \left(f(\varphi (x))\right)"=f_(u)"\left(\varphi (x_0) \right)\cdot \varphi"(x_0) $$

inak pre väčšiu skratku: $y_(x)"=y_(u)"\cdot u_(x)"$.

V akciách, ktoré som rozdelil, môžu všetky funkcie vyzerať $y=f(x)$ (preto vidíme len funkcie jednej zmeny $x$). Je zrejmé, že vo všetkých akciách je nesprávne vziať $y"$ na zmenu $x$. Napríklad tí, ktorí sú chytrí na zmenu $x$, často nahradia $y"$ $y"_x$.

Na zadkoch č. 1, č. 2 a č. 3 bola vyhotovená správa o procese oboznámenia sa s funkciami skladania. Butt č. 4 vymenovania pre väčšie pochopenie tabuliek druhej a môže byť rozumné.

Je potrebné dodržať krútenie materiálu v zadkoch č. 1-3, aby ste prešli na samostatné riešenie pažieb č.5, č.6 a č.7. Aplikujte č. 5, č. 6 a č. 7 na krátke rozhodnutie, aby si čitateľ mohol ihneď skontrolovať správnosť svojho výsledku.

Zadok #1

Nájdite podobnú funkciu $y=e^(\cos x)$.

Potrebujeme poznať presnú funkciu skladania $y"$. Ak $y=e^(\cos x)$, potom $y"=\left(e^(\cos x)\right)"$. Ak chcete vedieť, trik $ \ left(e^(\cos x)\right)"$ vyhrajte vzorec č. 6 z tabuliek podobného . Aby sme vyhrali formulu č. 6, je potrebné opraviť to, čo je podľa nášho názoru $u=\cos x$. Ďalej sa rozhodnutie aplikuje na banálne rozvodne vzorca č. 6, aby sa $\cos x$ namiesto $u$:

$$ y"=\left(e^(\cos x) \right)"=e^(\cos x)\cdot (\cos x)" \tag (1.1)$$

Teraz je potrebné poznať hodnotu virázy $(\cos x)"$. Vráťme sa k tabuľkám nižšie, z ktorých si vyberieme vzorec č. 10. Nahradením $u=x$ za vzorec č. 10, možno: $(\cos x)"=-\ sin x\cdot x"$. Teraz pokračujme v rovnosti (1.1), po jej pridaní nájdeme výsledok:

$$ y"=\left(e^(\cos x) \right)"=e^(\cos x)\cdot (\cos x)"= e^(\cos x)\cdot (-\sin x \cdot x") \tag (1.2) $$

Skіlki $x"=1$, potom môžeme pokračovať v rovnosti (1.2):

$$ y"=\left(e^(\cos x) \right)"=e^(\cos x)\cdot (\cos x)"= e^(\cos x)\cdot (-\sin x \cdot x")=e^(\cos x)\cdot (-\sin x\cdot 1)=-\sin x\cdot e^(\cos x) \tag (1.3) $$

Tiež z parity (1.3) môže byť: $y"=-\sin x\cdot e^(\cos x)$. 1.3) Neskôr bola nájdená podobná skladacia funkcia;

Vidpovid: $y"=-\sin x\cdot e^(\cos x)$.

Zadok #2

Nájdite nasledujúce funkcie $y=9\cdot \arctg^(12)(4\cdot \ln x)$.

Musíme vypočítať cenu $y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"$. Je príznačné, že konštanta (to je číslo 9) môže byť obviňovaná zo zlého znamenia:

$$ y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"=9\cdot\left(\arctg^(12)(4\cdot \ln x) \right)" \tag (2.1) $$

Teraz prejdime k viráze $\left(\arctg^(12)(4\cdot \ln x) \right)"$. Aby sme si vybrali vzorec z tabuliek podobných, je to jednoduchšie, budem prezentujte virázu, ktorá vyzerá takto: $\ left( \left(\arctg(4\cdot \ln x) \right)^(12)\right)"$. Teraz je jasné, že treba vyhrať formulu č.2, tobto. $\left(u^\alpha \right)"=\alpha\cdot u^(\alpha-1)\cdot u"$. Pre qiu môže byť vzorec reprezentovaný $u=\arctg(4\cdot \ln x)$ i $\alpha=12$:

Doplnenie rovnosti (2.1) sa od výsledku odpočíta, možno:

$$ y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"=9\cdot\left(\arctg^(12)(4\cdot \ln x) \right)"= 108\cdot\left(\arctg(4\cdot \ln x) \right)^(11)\cdot (\arctg(4\cdot \ln x))“ \tag (2.2) $$

V tejto situácii sa často povoľuje odpustenie, ak je prvou voľbou vzorec $(\arctg \; u)"=\frac(1)(1+u^2)\cdot u"$ nahradiť vzorec $\left (u^\ alpha \right)"=\alpha\cdot u^(\alpha-1)\cdot u"$. Na pravej strane je na vine prvá vec, ale pokhіdna zvnіshnyої fungujeії. Aby ste pochopili, keďže samotná funkcia sa bude volať pre výraz $\arctg^(12)(4\cdot 5^x)$, ukážte, že vám záleží na hodnote $\arctg^(12)(4\cdot 5^ x) $ pre akúkoľvek hodnotu $ x $. Začnite uhádnutím hodnoty $5^x$, potom vynásobte výsledok 4, odčítaním $4\cdot 5^x$. Teraz, vzhľadom na výsledok, vezmeme arkustangens a odčítame $arctg(4cdot 5^x)$. Potom vezmeme číslo v dvanástich krokoch a odčítame $ arctg (12) (4 cdot 5 x) $. Drž sa ďalej, - tobto. zvedennya v krokoch 12 - a bude mať rovnakú funkciu. A hneď ďalšou vecou bolo začať odmietnutie, ktoré bolo prerušené ekvivalenciou (2.2).

Teraz je potrebné poznať $(\arctg(4\cdot \ln x))"$. Môžeme vyhrať vzorec č. 19 z tabuliek podobných, pričom v ňom dosadíme $u=4\cdot \ln x$:

$$ (\arctg(4\cdot \ln x))"=\frac(1)(1+(4\cdot \ln x)^2)\cdot (4\cdot \ln x)" $$

Trochs možno ľahko odpočítať od virazu, vrahovoyuchi $(4\cdot \nn x)^2=4^2\cdot (\ln x)^2=16\cdot \ln^2 x$.

$$ (\arctg(4\cdot \ln x))"=\frac(1)(1+(4\cdot \ln x)^2)\cdot (4\cdot \ln x)"=\frac( 1)(1+16\cdot \ln^2 x)\cdot (4\cdot \ln x)" $$

Rovnosť (2.2) bude teraz vyzerať takto:

$$ y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"=9\cdot\left(\arctg^(12)(4\cdot \ln x) \right)"=\\ =108\cdot\left(\arctg(4\cdot \ln x) \right)^(11)\cdot (\arctg(4\cdot \ln x))“=108\cdot \left(\arctg(4\cdot \ln x) \right)^(11)\cdot \frac(1)(1+16\cdot \ln^2 x)\cdot (4\cdot \ln x)" \tag (2.3) $$

Vedieť $(4\cdot \ln x)"$ už nestačí. Za zlé znamenie obviňujeme konštantu (teda 4): $(4\cdot \ln x)"=4\cdot (\ln x)"$. aby ste poznali $(\ln x)"$ vyhrajte vzorec #8 tak, že v ňom nahradíte $u=x$: $(\ln x)"=\frac(1)(x)\cdot x"$. Ak $x"=1$, potom $(\ln x)"=\frac(1)(x)\cdot x"=\frac(1)(x)\cdot 1=\frac(1)(x) $. Po odčítaní výsledku od vzorca (2.3) odpočítame:

$$ y"=\left(9\cdot \arctg^(12)(4\cdot \ln x) \right)"=9\cdot\left(\arctg^(12)(4\cdot \ln x) \right)"=\\ =108\cdot\left(\arctg(4\cdot \ln x) \right)^(11)\cdot (\arctg(4\cdot \ln x))“=108\cdot \left(\arctg(4\cdot \ln x) \right)^(11)\cdot \frac(1)(1+16\cdot \ln^2 x)\cdot (4\cdot \ln x)" =\\ =108\cdot \left(\arctg(4\cdot \ln x) \right)^(11)\cdot \frac(1)(1+16\cdot \ln^2 x)\cdot 4\ cdot \frac(1)(x)=432\cdot \frac(\arctg^(11)(4\cdot \ln x))(x\cdot (1+16\cdot \ln^2 x)).$

Tipujem, že funkcie skladania sa najčastejšie nachádzajú v jednom rade - ako sa píše vo zvyšku rovnosti. Preto pri zostavovaní typických rozrahunkіv alebo riadiacich robotov nie je povinné vypracovať riešenie tak podrobne.

Vidpovid: $y"=432\cdot \frac(\arctg^(11)(4\cdot \ln x))(x\cdot (1+16\cdot \ln^2 x))$.

Zadok #3

Poznať funkcie $y"$ $y=\sqrt(\sin^3(5\cdot9^x))$.

Pre cob troch zmeníme funkciu $y$ pridaním radikálu (koreň) v tom istom kroku: $y=\sqrt(\sin^3(5\cdot9^x))=\left(\sin(5\) cdot 9^x) \right)^(\frac(3)(7))$. Teraz poďme na to zlé. $y=\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))$, potom:

$$ y"=\left(\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))\right)" \tag (3.1) $$

Dobytie vzorca č. 2 z tabuliek podobných, dosadením v ňom $u=\sin(5\cdot 9^x)$ i $\alpha=\frac(3)(7)$:

$$ \left(\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))\right)"= \frac(3)(7)\cdot \left( \sin(5\cdot 9^x)\right)^(\frac(3)(7)-1) (\sin(5\cdot 9^x))"=\frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) (\sin(5\cdot 9^x))" $$

Prodovzhimo rivnist (3.1), vikoristuyuchi odpočítaním výsledku:

$$ y"=\left(\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))\right)"=\frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) (\sin(5\cdot 9^x))" \tag (3.2) $$

Teraz je potrebné poznať $(\sin(5\cdot 9^x))"$. Vzorec č. 9 je možné vyhrať z tabuliek podobných dosadením $u=5\cdot 9^x$ v ňom:

$$ (\sin(5\cdot 9^x))"=\cos(5\cdot 9^x)\cdot(5\cdot 9^x)" $$

Pridaním rovnosti (3.2) k výsledku môžeme:

$$ y"=\left(\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))\right)"=\frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) (\sin(5\cdot 9^x))"=\\ =\frac(3) (7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) \cos(5\cdot 9^x)\cdot(5\cdot 9 ^x)" \tag (3.3) $$

Zabudli ste vedieť $(5\cdot 9^x)"$. V prípade klasu obviňujeme konštantu (číslo $5$) za znamienko podobného, ​​potom $(5\cdot 9^x)"=5\cdot (9^x) "$. Pre hodnotu podobného $(9^x)"$ vytvoríme vzorec č. 5 z tabuliek podobných, pričom dosadíme $a=9$ a $u=x$ pred ním: $(9^x)"=9^x\cdot \ ln9\cdot x"$. Ak $x"=1$, potom $(9^x)"=9^x\cdot \ln9\cdot x"=9^x\cdot \ln9$. Teraz môžeme pokračovať s rovnosťou (3.3):

$$ y"=\left(\left(\sin(5\cdot 9^x)\right)^(\frac(3)(7))\right)"=\frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) (\sin(5\cdot 9^x))"=\\ =\frac(3) (7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) \cos(5\cdot 9^x)\cdot(5\cdot 9 ^x)"= \frac(3)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7)) \cos(5\cdot 9 ^x)\cdot 5\cdot 9^x\cdot \ln9=\\ =\frac(15\cdot \ln 9)(7)\cdot \left(\sin(5\cdot 9^x)\right) ^(-\frac(4)(7))\cdot \cos(5\cdot 9^x)\cdot 9^x. $$

Kroky môžete opäť obrátiť na radikály (to je koreň) napísaním $\left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7))$ pohľadom $\frac( 1 )(\left(\sin(5\cdot 9^x)\right)^(\frac(4)(7)))=\frac(1)(\sqrt(\sin^4(5\) cdot 9 ^x)))$. Potom to bude napísané v tomto tvare:

$$ y"=\frac(15\cdot \ln 9)(7)\cdot \left(\sin(5\cdot 9^x)\right)^(-\frac(4)(7))\cdot \cos(5\cdot 9^x)\cdot 9^x= \frac(15\cdot \ln 9)(7)\cdot \frac(\cos (5\cdot 9^x)\cdot 9^x) (\sqrt(\sin^4(5\cdot 9^x))).$$

Vidpovid: $y"=\frac(15\cdot \ln 9)(7)\cdot \frac(\cos (5\cdot 9^x)\cdot 9^x)(\sqrt(\sin^4(5\) ) cdot 9^x)))$.

Zadok #4

Ukážte, že vzorce č. 3 a č. 4 z tabuliek sú podobné a posledné zo vzorcov č. 2 z tabuliek.

Vzorec č. 2 z nižšie uvedených tabuliek má podobnú funkciu $u^\alpha$. Nahradením $\alpha=-1$ za vzorec č. 2, vezmeme:

$$(u^(-1))"=-1\cdot u^(-1-1)\cdot u"=-u^(-2)\cdot u"\tag (4.1)$$

Ak $u^(-1)=\frac(1)(u)$ i $u^(-2)=\frac(1)(u^2)$, potom rovnosť (4.1) možno prepísať takto: $ \ left(\frac(1)(u) \right)"=-\frac(1)(u^2)\cdot u"$. Tse a є vzorec č. 3 tabuľky podobných.

Som znovnemosya až do vzorca č. 2 z tabuliek horšieho. Predstavme si až $\alpha=\frac(1)(2)$:

$$\left(u^(\frac(1)(2))\right)"=\frac(1)(2)\cdot u^(\frac(1)(2)-1)\cdot u" =\frac(1)(2)u^(-\frac(1)(2))\cdot u"\tag (4.2) $$

Skіlki $u^(\frac(1)(2))=\sqrt(u)$ i $u^(-\frac(1)(2))=\frac(1)(u^(\frac( 1) )(2)))=\frac(1)(\sqrt(u))$, potom možno rovnosť (4.2) prepísať takto:

$$ (\sqrt(u))"=\frac(1)(2)\cdot \frac(1)(\sqrt(u))\cdot u"=\frac(1)(2\sqrt(u) )\cdot u" $$

Otrimanova rovnosť $(sqrt(u))"=\frac(1)(2sqrt(u))cdot u"$ i є vzorec č. 4 tabuliek podobných. Podobne ako Bachite, vzorce č. 3 a č. 4 z tabuliek sú podobné vzorcom č. 2 nahradením podobnej hodnoty $ alfa $.