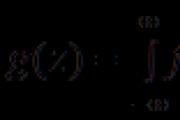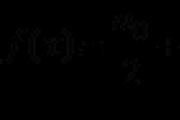Razkladannya v vrsti fur'є fantje in neparne funkcije neučinkovitost bezsel parseval. Riadi Fur'є: Zgodovina in infuzija matematičnega mehanizma na razvoj znanosti

Riadi Fur'є - cena dokaj prevzete funkcije z določenim obdobjem iz vrstice viglyadi. Pri gledalcu, obrnjenem navzven, se rešitev imenuje postavitev elementa na ortogonalni osnovi. Izvajanje funkcij za številne Fur'є dopolniti z napenjanjem orodij pri razvoju razvojnih delavcev organom te ponovne implementacije z integracijo, diferenciacijo, pa tudi z uporabo argumentov in argumentov.

Lyudin, ki ne ve ničesar o matematiki, pa tudi o koreninah francoskega zvarjenega Fur'є, ki je boljši za vse, ne za zvok, ampak za "vrsto" in za katerega je potreben smrad. In medtem je proces ponovne uprizoritve do konca prešel v naše življenje. Ne očitajo brez matematike, ampak fizike, kemije, zdravnikov, astronomov, seizmologov, oceanografije in mnogih drugih. Spoznajmo se pobližje s predniki velikega francoskega vinarja, kot bi utrinek joka, saj je bila ura pred nami.

Lyudina tista reinkarnacija Fur'є

Serija Fur'є є v eni od metod (red analize in іnshim) Proces se ustvari z zvokom, če ima oseba zvok. Naše vuho v avtomatskem načinu je poustvarjanje elementarnih delcev v vzmetnem središču, ki je položeno v vrstico (izven spektra) zadnje dnevne vrednosti čistosti za tone rasti. Oddaljeni um poustvarja poklon zvokom, ki smo jih prejeli. Vse naloge morajo biti obkrožene z našim poznavanjem dokazov, same po sebi, in da bi razumeli proces, je treba to znati narediti v matematiki.

Poročilo o preoblikovanju Fur'є

Reinkarnacijo Fur'є lahko izvedemo z analitičnimi, numeričnimi in inshim metodami. Številni Fur'є se nanašajo na numerično metodo določanja kakršnih koli kolivalnih procesov - od oceanskih plimovanja in rahlega mrzlica do ciklov zaspanih (tistih astronomskih objektov) aktivnosti. Možno je izbrati funkcije, ki predstavljajo številne sinusne procese shranjevanja, kot je niz sinusnih skladišč, ki se premikajo od minimalnega do maksimuma in nazaj. Ponovna izvedba funkcije Fur'є, ki opisuje fazo in amplitudo sinusoidov, ki prikazujejo frekvence petja. Celoten proces je lahko zmagovit za razvoj še bolj zložljivih rivnjanov, ki opisujejo dinamične procese, ki izhajajo iz toplote, svetlobe in električne energije. Prav tako številna Fur'є omogočajo vizualizacijo neprekinjenih skladišč pri prepogibnih kolizijskih signalih, zaradi česar je postalo mogoče pravilno interpretirati eksperimentalne previdnostne ukrepe v medicini, kemiji in astronomiji.

Zgodovinska izjava

Oče-oče teorije je francoski matematik Jean Bathist Joseph Fur'є. Yogo im'yam zgod i bulo se imenuje poustvarjanje. V tej metodi je bila najdena zbirka idej za implantacijo in razlago mehanizmov toplotne prevodnosti – širjenja toplote v trdnih telesih. Fur'є, pusti ga, s posipom nepravilnih izrastkov, je mogoče razporediti po najpreprostejši sinusoidi, minimalni in maksimalni temperaturi kože ter lastni fazi. Pri širokem razponu kože se takšna komponenta izgubi od najmanjše do največje nazaj. Matematična funkcija, ki opisuje zgornji in spodnji vrh krivulje, pa tudi fazo kožnih harmonik, se je imenovala ponovno ustvarjanje Fur'є v obliki dviga temperature. Avtor teorije izven škatle funkcije, saj je pomembno, da se držimo matematičnega opisa, še bolj priročnega v nizu kosinusov in sinusov, a v seštevku podamo izven- vtičnica škatle.

Načelo ponovne uprizoritve in pogled na zabavo

Udeleženci zgodovine matematike – najzgodnejši matematiki 19. stoletja – teorije niso sprejeli. Glavne trditve Fur'a je podal o tistih, ki imajo funkcijo, kako opisati premico ali krivuljo, kako odpreti, je mogoče plačati davke na seštevek sinusnih valov, ki so brez prekinitve. Jakov zadnjico lahko vidite Heaviside "zbor". Kakovost funkcije je posledica kopičenja električnega brenčanja iz časa dneva, ko je lantsug zmeden. Takratni udeleženci teorije se takšne situacije niso držali, čeprav je bil viraz opisan s kombinacijo neponovljivih, izjemnih funkcij, kot so eksponent, sinusoida, črta je abokvadratna.

Zakaj je teorija Fura koristila francoskim matematikom?

Tudi če matematika zanima njegova trdnost, potem, če obstaja neskončna trigonometrična serija Fur'є, je mogoče natančneje razbrati manifestacijo pogostega obrata pri takšnem padcu, kot da tega ni. . Na uho 19. stoletja se je trdnost zdela absurdna. Čeprav nepomembno v vsem znanju, je veliko matematikov razširilo področje uvajanja pojava in ga oživilo v zadnjih nekaj letih toplotne prevodnosti. Večinoma se je večina učencev borila za hrano: "Kako se lahko vsota sinusne vrste približa natančni vrednosti porazdelitvene funkcije?"

Podobnost vrstic Fur'є: zadnjica

Prehrana o potrebi po dodatnih številkah. Za bolj udoben pojav je vidna klasična zadnjica. Bi zmogli, če ne gre priti do točke, kako bo suha ofenzivna krokodila najmanjša za naslednjega? Recimo, da ste dva metra oddaljeni od ceste, krokus je blizu polovice, ofenziva je do oznake tri četrt, po naslednji pa pridete do 97. ceste. Vendar besedi b in v nista bili krivi, načrtovane oznake ne boste dosegli v strogem matematičnem smislu. Z uporabo številčne rosrahunke je mogoče prinesti, da se je z dovoljenjem mogoče približati najmanjšemu nizu podatkov. Danska dokazuje, da je enakovredna dokazovanju dejstva, da bo skupna vrednost enega drugega, ene četrtine, pragmatična le za enega.

Prehrana podjetja: prijatelj, ki prihaja, za Prilad Lorda Kelvina

Cena hrane se je ponovila ob koncu devetnajstega stoletja, saj so številni Fur'є poskušali zasosuvati napovedati intenzivnost povečane in visoke plime. Ob koncu ure je bil priložen Lord Kelvin buv vinaydeny, ki je analogni številčni nastavek, ki je mornarjem ruske in trgovske flote omogočil prikaz naravnega pojava. Danski mehanizem z začetkom rekrutiranja faz in amplitud po tabelah frekvence flushov in trenutnih časovnih trenutkov, ki so začasno zamrznjeni v tem pristanišču, ki se razteza do skale. Parameter kože ima sinusno komponento viraz pretoka in eno od rednih skladišč. Rezultati vimiryuvana so bili uvedeni v račun Lorda Kelvina, ki je sintetiziral krivuljo, ki je višino prednosti prenesla na funkcijo ofenzivne usode ekipe. Nevsiljive krivulje balinanja so zložene v vseh pristaniščih sveta.

In kako bo proces uničil maloprodajna funkcija?

Tisti uri je postalo očitno, da je v redu, da se prenaša v izlivno bolezen, zaradi velikega števila elementov v rakunki lahko preštejete veliko število faz in amplitud in tako preprečite natančnejši prenos. Protest se je pojavil, da ne naleti na pravilnost pri tihih ljudeh, če plimski viraz, ki je drsnik sinteze, razkriva močan stribok, da bo rožnat. Hkrati, če je treba vnesti podatke iz tabel časovnih trenutkov, potem je nemogoče izračunati število decilkoh stopenj Fur'є. Posebna funkcija je posodobljena na sinusne komponente (glede na znano zmogljivost). Robustnost med odhodnim in obnovljivim virom je možna na kateri koli točki. Pri ponovnem izračunu te odredbe je razvidno, da se vrednost največjega odpuščanja ne spremeni. Vendar je smrad lokaliziran na območju, kjer bo pokazal točko rezanja, in če je bistvo, bo zgrešil nič. Leta 1899 je bil potrjen rezultat teoretične potrditve Joshue Willarda Gibbsa z univerze Ulsky.

Podobnost serije Fur'є in razvoj matematike na splošno

Analiz Fur'є ne stagnira do odmorov, temveč do neskončnega števila pljusk na intervalu petja. V celi seriji Fur'є je funkcija storža predstavljena z rezultatom resničnega fizičnega vimirja, ki se vedno zbližuje. Prehrana danega procesa za določene razrede funkcij je bila pripeljana do pojava novih vej matematike, na primer teorije družbenih funkcij. Vona je povezana z imeni, kot so L. Schwartz, J. Mikusinsky in J. Temple. V okviru teorije Bula je določeno branje in natančna teoretična osnova za takšne vire, kot je Diracova delta funkcija (opisal bom območje enega samega območja, skoncentriranega na neskončno majhnem obrobju točka) in "korak" Hevіraza. Režiserji robotske serije Fur'є so se zatekli za oddajanje podeželskih in industrijskih zgradb, v katerih je figura intuitivnega: točkovni naboj, točkovna masa, magnetni dipoli, pa tudi sistem za razporeditev na balti.

Krzna metoda є

Serija Fur'є, v skladu z načeli motenj, je mogoče popraviti z zlaganjem zložljivih oblik večje preprostosti. Na primer, spremembo toplotnega toka razložimo s prehodom s prehodom iz toplotnoizolacijskega materiala v napačno obliko, bodisi z zlobno površino zemlje - z zemljo, s serpentinasto orbito neba - s dotok planetov. Praviloma je malo ryvnyannya, kako opisati preprost klasični sistem, za osnovno odkrivanje kožnih stanj. Fur'є, ki kaže, da lahko preprosto rešitev uporabimo tudi za zanikanje več zložljivih zgradb. Vislovlyuyuchis moja matematika, serija Fur'є - celotna metoda predložitve vrtljive vsote harmonikov - kosinusoida in sinusoida. V ta namen je analiza vidomij tudi za namen »harmonične analize«.

Številne Fur'є - idealna tehnika za "računalniško dobi"

Pred vzpostavitvijo računalniške tehnologije je bila metodologija Fur'є Bull najlepši dodatek k arzenalom vseh robotov z naravo naše svetlobe. Število Fur'є v kompleksni obliki omogoča, da virishuvati ni prikrajšan za preprostost podjetja, saj je mogoče neposredno ovirati zakone Newtonove mehanike, temveč temeljna načela. Večina vpogledov v newtonsko znanost devetnajstega stoletja je postala več kot dovolj za poznavanje metodologije Fur.

Riadi Fur'є seogodnі

Z razvojem računalnikov, s prenovo Fur'є je prišlo do očitno novega rivn. Ta metodologija je bila razvita praktično na vseh področjih znanosti in tehnologije. Zadka jaka lahko usmerjate digitalni avdio in video signal. Izvajanje joga je postalo zanič odvzem teorije, saj je francoski matematik razbil na storž 19. stoletja. Torej, število Fur'є v kompleksni obliki, ki omogoča rast luknje v vivchenna kozmičnem prostoru. Poleg tega je bila cena povezana z razvojem fizike prevodnih materialov in plazme, mikrokromne akustike, oceanografije, radijskega lociranja in seizmologije.

Trigonometrična serija Fur'є

V matematiki serija Fur'є є na način definiranja zadostnih zložljivih funkcij z vsoto preprostih. V obrobnih vipadah je lahko število takšnih virazov neskončno. Če je med postopkom več kot količina škode, je natančneje dobiti končni rezultat. Najpogosteje je to najpreprostejša vikoristična trigonometrična funkcija kosinusa ali sinusa. V takšni seriji se Fur'є imenujejo trigonometrični, prikaz takšnih variacij pa se imenuje harmonična porazdelitev. Celotna metoda vizualizacije v matematiki. Spredaj je predvidena trigonometrična serija za sliko, pa tudi uvedba funkcij, glavnega aparata teorije. Poleg tega vino dopušča pomanjkanje znanja matematične fizike. Nareshty, celotna teorija je šla do dna razvoja še pomembnejših vej matematične znanosti (teorija integralov, teorija periodičnih funkcij). Poleg tega je služil kot prava točka za razvoj ofenzivnih funkcij dinamične spremembe, pa tudi za zajemanje harmonične analize.

Niz periodičnih funkcij Fur'є iz obdobja 2π.

Številne Fur'є omogočajo periodične funkcije, ki jih je mogoče zložiti na komponente. Menjava drsnikov in vzmeti, zamenjava, hitrost in pospeševanje mehanizmov ročične ojnice in akustičnih hvili - vse vrste praktičnega zadka shranjevanja periodičnih funkcij v inženirskih seznamih.

Postavitev v vrsto Fur'є, ki teče na nizu, vendar vse funkcije, vendar praktično smiselne v intervalu -π ≤x≤ π, se je mogoče premikati v pogledu podobnih trigonometričnih vrstic (število podobnih členov, po

Standardni (= zvychany) zapis skozi vsoto sinx in cosx

f (x) = a o + a 1 cosx + a 2 cos2x + a 3 cos3x + ... + b 1 sinx + b 2 sin2x + b 3 sin3x + ...,

de a o, a 1, a 2, ..., b 1, b 2, .. - Referenčne konstante, tobto.

De za razpon od -π do π do zmogljivosti števila Fur'є, ki se plača po formulah:

Značilnosti a o, a n і b n imenovan kofіtsієntami Fur'є, in če je mogoče vedeti, se imenuje vrsta (1). naroči krzno, s funkcijo f (x). Za serijo (1) se izraz (a 1 cosx + b 1 sinx) imenuje prvi oz glavna harmonika,

Najboljši način za zapisovanje vrstice je viktorijanski sp_vvidnoshennya acosx + bsinx = csin (x + α)

f (x) = a o + c 1 sin (x + α 1) + c 2 sin (2x + α 2) + ... + c n sin (nx + α n)

De ao je konstanta, s 1 = (a 1 2 + b 1 2) 1/2, sn = (an 2 + bn 2) 1/2 je amplituda drugih komponent, za cesto pa an = arctan an / b n.

Za serijo (1) se izraz (a 1 cosx + b 1 sinx) ali c 1 sin (x + α 1) imenuje prvi oz. glavna harmonika,(a 2 cos2x + b 2 sin2x) ali c 2 sin (2x + α 2) se imenuje druga harmonika in tako daleč.

Za natančno zaznavanje zložljivega signala je potrebno neomejeno število članov. Vendar ima praktično osebje bagatyokha dovolj škropljenja prvih članov.

Niz Fur'є neperiodičnih funkcij iz obdobja 2π.

Porazdelitev neponavljajočih se funkcij.

Ker funkcija f (x) ni periodična, to pomeni, da je ni mogoče postaviti v vrstico Fur'є za vse vrednosti x. Vendar pa je mogoče narediti število Fur'є, ki predstavlja funkcijo v katerem koli obsegu s širino 2?

Če je nastavljena neperiodična funkcija, je mogoče dodati novo funkcijo, vrednost f (x) v območju petja zavibrira in položaj se ponovi z razponom z intervalom 2π. Nihanja so nova funkcija є periodična s periodo 2π, її lahko razširimo na vrstico Fur'є za vse vrednosti. Na primer, funkcija f (x) = x ni periodična. Če pa je potrebno razširiti її v vrstici Fur'є na interval od do 2π, bo položaj intervala periodična funkcija z obdobjem 2π (kot je prikazano na spodnji sliki).

Za neperiodične funkcije, kot je f (x) = x, je vsota števila Fur'є ustrezna vrednost f (x) na vseh točkah danega območja, ne pa f (x) za točke na položaju obsega. Za poznavanje številnih Fur'є neperiodičnih funkcij v območju 2π se uporablja enaka formula koeficientov Fur'є.

Seznanjene in neparne funkcije.

Recimo, funkcija y = f (x) parna kjer je f (-x) = f (x) za vse vrednosti x. Grafi parnih funkcij temeljijo na simetričnih funkcijah (prikazane v zrcalu). Dve seznanjeni funkciji: y = x 2 і y = cosx.

Recimo, da je funkcija y = f (x) neparno kjer je f (-x) = - f (x) vse vrednosti x. Grafi neparnih funkcij so odvisni od simetričnih koordinat.

Bagato funkcije niso fantje, niso neparni.

Razširitev v vrsti Fur'є v kosinus.

Niz Fur'є seznanjenih periodičnih funkcij f (x) s periodo 2π lahko odstrani člane iz kosinusov (da ne odstrani članov iz sinusov), vključite pa lahko tudi stalnega člana. Otzhe,

de kofizinti številne Fur'є,

Serija Fur neparne periodične funkcije f (x) s periodo 2π je zamenjava členov s sinusi (da se članom ne maščujejo s kosinusi).

Otzhe,

de kofizinti številne Fur'є,

Vrstica Fur'є na pivperiodi.

Ker je funkcija namenjena razponu, recimo od 0 do π, in ne samo od 0 do 2π, jo lahko postavimo v vrsto samo s sinusi ali samo kosinusi. Otrimaniy število Fur'є se imenuje naročilo Fur'є na napіvperіodі.

Treba je popraviti porazdelitev Fur'є na napivperiodi na kosinusih funkcijo f (x) v območju od 0 do π, je treba dodati par periodičnih funkcij. Na sl. Spodaj je prikazana funkcija f (x) = x, ki se zahteva v intervalu od x = 0 do x = π. Nihanja parne funkcije so simetrična, vendar os f (x) vodi AB črta, ki je prikazana na sl. nižje. Pustite ga, vendar se drža pogledanega intervala občasno obrezuje v trikotno obliko ê s periodo 2π, nato se prikaže okvirna grafika. na sl. nižje. Oscilacije so potrebne, da se odšteje postavitev Fur'є v kosinusih, kot tudi prej izračunana učinkovitost Fur'є a o і a n

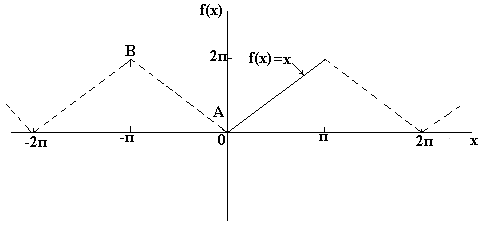
Treba je popraviti porazdelitev Fur'є na napіvperіodі za sinusov funkcija f (x) v območju od 0 do π, je treba imeti neparno periodično funkcijo. Na sl. Spodaj je prikazana funkcija f (x) = x, ki se zahteva v intervalu od x = 0 do x = π. Nihanja so neparna, funkcija je simetrična glede na storž koordinat, to bo črta CD, kot je prikazano na sl. Samo pustite ga, toda položaj periodičnega signala, podobnega datoteki, s periodo 2π, drža datotečnega signala s periodo 2π, nato pa odčitki na sl. Za porazdelitev Furina na podlagi sinusov je treba zavrniti nihanja, tako prej kot prej, izračunano po vrednosti Fur. b

Število Fur'є za pred-interval.

Razširitev periodičnih funkcij iz obdobja L.

Periodična funkcija f (x) se ponavlja iz prirastkov x L, torej. f (x + L) = f (x). Če se premaknete od funkcij, ki so bile predhodno prikazane iz obdobja 2π, na funkcije iz obdobja L, da dokončate preprosto, lahko nekaj od tega naredite za dodatno spremembo spremembe.

Kako spoznati vrsto Fun'є funkcije f (x) v območju -L / 2≤x≤L / 2, uvedemo novo spremembo u v takem rangu, da je funkcija f (x) majhna perioda 2π in potem u. Če je u = 2πx / L, potem je x = -L / 2 za u = -π in x = L / 2 za u = π. Prav tako ne pustite, da je f (x) = f (Lu / 2π) = F (u). Serija Fur'є F (u) maє viglyad

(Med integracijo je mogoče nadomestiti kateri koli interval do L, na primer od 0 do L)

Niz Fur'є za napіvperiodo za funkcije, določene v intervalu L ≠ 2π.

Za namestitev u = πх / L je interval od x = 0 do x = L od intervala od u = 0 do u = π. Torej, funkcijo je mogoče v vrsti razširiti samo s kosinusom ali samo s sinusom, tobto. v vrstica Fur'є na pivperiodi.

Razširitev kosinusov v območju od 0 do L ma viglyad

Riadi Fur'є- način predstavitve funkcije zlaganja z vsoto preprostih in dobrih.
Sinus in kosinus - periodične funkcije. Tudi smrad ortogonalne osnove. Moč Qiu je mogoče razložiti po analogiji z osmi X X Xі Y Y Y na koordinatnem območju. Torej, kot lahko opišemo koordinate točke vzdolž osi, lahko opišemo, ali je funkcija obeh sinusov in kosinusov. Trigonometrične funkcije se je enostavno naučiti iz matematike.

Videz sinusa in kosinusa je možen za gledalca takega hwila:

Sinus - tse kosinus, chervonі - sinus. Imenujejo jih tudi harmoniki. Kosinusi so fantje, sinusi so neparni. Izraz harmonično izvira iz antike in oblačenja ter opozorila o medsebojni povezanosti zvokov iz glasbe.

Sho tudi veslaj Fur'є

Takšen niz, saj je najlažje opisati funkcijo sinusa in kosinusa, se imenuje trigonometričen. Poimenovan v čast svojega ljubitelja vina Jeana Batista Josepha Fur'є, na primer XVIII - ušesa XIX stoletja. nekako dokazati, da, ali je mogoče funkcijo predstaviti v viglyadu, kombinacijo takšnih harmonikov. In bolj ko ga vzameš, več ga vzameš, več ga vzameš. Slika je na primer nižja: mogoče je pikati, z velikim številom harmonikov, torej člani so nizki Fur'є, rdeči graf je dovolj star, da je bližje modremu - wicked funkcija.

Praktično skladiščenje pri grenkem svitі

In kaj je s porabo večkrat? Kako se lahko zataknete na praktičen in praktičen način? Vyavlyayetsya, Fur'є k temu in vidomy za ves svet, toda praktičen cimet jogo ljubezni je dobesedno nerazvrščen. Oh, tam je enostavno popraviti, de be-yaki chi khvili: tudi akustika, astronomija, radijska tehnika. bud. Najpreprostejša zadnjica yogo victoriannya: mehanizem robota in kamere ter video kamere. V krajšem času bom razložil, da ni mogoče dodati samo slik, ampak izvedba serije Fur's. І pratsyuє tse skrіz - eno uro gledanje slik v internetu, film ali poslušanje glasbe. Članek lahko preberete s svojega mobilnega telefona, če ste ljubitelj Fur'є vi rangov. Brez ponovnega izuma Fur'є nismo dobili najboljše internetne pasovne širine, ampak samo poglejte videoposnetek na YouTubu in si oglejte standardno kakovost.

Na celotni shemi dvosvetovne preobrazbe Fur'є, kot vikoristovuyutsya za distribucijo slike na harmonike, tako da so osnovna skladišča. Na diagramu je vrednost -1, bilim kodirana s črno, desno in dol za grafom se frekvenca povečuje.

Zagon v vrsti Fur'є

Singerly, vzhe vzhe vtomilsya prebrati, enako velja za formule.
Za tak matematični pristop, kot je porazdelitev funkcij v vrstici Fur'є, sta brata integrirana. Bagato Integral Pri izključenem viglyadu napišem vrstico Fur'є ob viglyadu neskončnega sumija:

F (x) = A + ∑ n = 1 ∞ (an cos ⁡ (nx) + bn sin ⁡ (nx)) f (x) = A + \ displaystyle \ sum_ (n = 1) ^ (\ infty) (a_n \ cos (nx) + b_n \ sin (nx))f (x) =A +n = 1∑ ∞ ​ (a n​ cos (n x) +b n​ greh (n x))
de
A = 1 2 π ∫ - π π f (x) d x A = \ frac (1) (2 \ pi) \ displaystyle \ int \ limits _ (- \ pi) ^ (\ pi) f (x) dxA =2 π1 ​ − π ∫ π ​ f (x) d x
an = 1 π ∫ - π π f (x) cos ⁡ (nx) dx a_n = \ frac (1) (\ pi) \ displaystyle \ int \ limits _ (- \ pi) ^ (\ pi) f (x) \ cos (nx) dxa n​ = π 1 ​ − π ∫ π ​ f (x) cos (n x) d x
bn = 1 π ∫ - π π f (x) sin ⁡ (nx) dx b_n = \ frac (1) (\ pi) \ displaystyle \ int \ limits _ (- \ pi) ^ (\ pi) f (x) \ sin (nx) dxb n​ = π 1 ​ − π ∫ π ​ f (x) sin (n x) d x

Možno je imeti neskončno število krat. a n a_n a n​ і b n b_n b n​ (Diši in se imenujejo konference za distribucijo Fur'є, A A A- tse samo po distribuciji), potem bodo številne napake v rezultatu 100 % shranjene iz izhodne funkcije f (x) f (x) f (x) na podlagi - π - \ pi − π prej π \ pi π ... To je primer artikulacije moči integracije sinusa in kosinusa. Čim več n n n Za vsako zasnovo funkcij bo porazdelitev funkcij v vrsti natančnejša.

zadnjico

Enostaven za uporabo y = 5 x y = 5x y =5 x
A = 1 2 π ∫ - π π f (x) dx = 1 2 π ∫ - π π 5 xdx = 0 A = \ frac (1) (2 \ pi) \ displaystyle \ int \ limits _ (- \ pi) ^ (\ pi) f (x) dx = \ frac (1) (2 \ pi) \ displaystyle \ int \ limits _ (- \ pi) ^ (\ pi) 5xdx = 0A =2 π1 ​ − π ∫ π ​ f (x) d x =2 π1 ​ − π ∫ π ​ 5 x d x =0
a 1 = 1 π ∫ - π π f (x) cos ⁡ (x) dx = 1 π ∫ - π π 5 x cos ⁡ (x) dx = 0 a_1 = \ frac (1) (\ pi) \ displaystyle \ int \ omejitve _ (- \ pi) ^ (\ pi) f (x) \ cos (x) dx = \ frac (1) (\ pi) \ displaystyle \ int \ limits _ (- \ pi) ^ (\ pi ) 5x \ cos (x) dx = 0a 1 ​ = π 1 ​ − π ∫ π ​ f (x) cos (x) d x =π 1 ​ − π ∫ π ​ 5 x cos (x) d x =0
b 1 = 1 π ∫ - π π f (x) sin ⁡ (x) dx = 1 π ∫ - π π 5 x sin ⁡ (x) dx = 10 b_1 = \ frac (1) (\ pi) \ displaystyle \ int \ limits _ (- \ pi) ^ (\ pi) f (x) \ sin (x) dx = \ frac (1) (\ pi) \ displaystyle \ int \ limits _ (- \ pi) ^ (\ pi ) 5x \ sin (x) dx = 10b 1 ​ = π 1 ​ − π ∫ π ​ f (x) sin (x) d x =π 1 ​ − π ∫ π ​ 5 x sin (x) d x =1 0
a 2 = 1 π ∫ - π π f (x) cos ⁡ (2 x) dx = 1 π ∫ - π π 5 x cos ⁡ (2 x) dx = 0 a_2 = \ frac (1) (\ pi) \ displaystyle \ int \ limits _ (- \ pi) ^ (\ pi) f (x) \ cos (2x) dx = \ frac (1) (\ pi) \ displaystyle \ int \ limits _ (- \ pi) ^ ( \ pi ) 5x \ cos (2x) dx = 0a 2 ​ = π 1 ​ − π ∫ π ​ f (x) cos (2 x) d x =π 1 ​ − π ∫ π ​ 5 x cos (2 x) d x =0
b 2 = 1 π ∫ - π π f (x) sin ⁡ (2 x) dx = 1 π ∫ - π π 5 x sin ⁡ (2 x) dx = - 5 b_2 = \ frac (1) (\ pi) \ displaystyle \ int \ limits _ (- \ pi) ^ (\ pi) f (x) \ sin (2x) dx = \ frac (1) (\ pi) \ displaystyle \ int \ limits _ (- \ pi) ^ (\ pi) 5x \ sin (2x) dx = -5b 2 ​ = π 1 ​ − π ∫ π ​ f(x) greh(2 x) dx= π 1 ​ − π ∫ π ​ 5 xgreh(2 x) dx= − 5

tako daleč sem. S takšno funkcijo lahko takoj rečemo, da vse a n = 0 a_n = 0an​ = 0 , kofіtsієнti b n b_nbn​ slučajno šteje. Yakshho mi vizmemo pershi chotiri so člani razporejeni v vrsto Fur'є za funkcijo y = 5 x y = 5xy= 5 x, Ogledamo:

$5x\approx 10\cdot \mathrm{greh}(x)-5\cdot \mathrm{greh}(2\cdot x)+310\cdot \mathrm{greh}(3\cdot x)-25\cdot \mathrm{greh}(4\cdot x)$

Graf funkcije, ki je vstopil, bo gledal ofenzivni rang:

Zagon, scho je šel, v vrsti Fur'є se približal naši funkciji iz škatle. Ker je več članov zapored, na primer 15, potem je bolj verjetni naslednji korak:

Več članov zapored, bolj natančno.
Vendar pa je lestvica grafa spremenljiva, mogoče je opaziti še eno značilnost ponovne implementacije: nizek Fur'є - periodična funkcija s točko 2 π 2 \ pi2 π .

V takem rangu si lahko predstavljate, ali gre za funkcijo, kot je ê brez prekinitve [- π; π] [- \ pi; \ pi][ − π ; π ] ... Vsa cena je nujna, da lahko analiziramo, kako se videz analizira, in da se opiše s funkcijami zlaganja. Nočem biti analitičen (tobto za formulo), izgubil bom, nimam pa nobenih težav z naborom sinusov in težav. Večino časa ga je mogoče prikazati do več Fur'є, najpogosteje pa ga je mogoče analitično prikazati na preprostih modelih, enem iz aplikacije nekaterih in seriji Fur'є.

Prepis

1 MINISTRSTVO ZA OCENJEVANJE ZNANOSTI RF NOVOSIBIRSKY DERŽAVNIJ UNIVERZA FIZIČKE FAKULTETE R.K.BELKHEVA RAZPET KRZNA V APLIKACIJAH IN TEŽAVAH Navchalnyi posibnik1

2 UDC BBK V161 B44 B44 Belkhєєva R.K. držati un-t. Novosibirsk, s. ISBN Na začetku obiska zmaga glavni gledalec serije Fur'є; Podrobna zasnova zadnjice za metodo Fur'є pred reševanjem problemov o prečni struni. Priloženo ilustrativno gradivo. Є zavdannya neodvisna rešitev. Naloge za študente in zmage na Fakulteti za fiziko NSU. Postanite prijatelj v metodičnem odboru Virishenna Fakultete za fiziko NSU. Recenzent dr. fiz. znanosti. V. A. Aleksandrov Zbirka priprav v okviru izvajanja Programa razvoja NDU-NSU na pp. ISBN s Novosibirska državna univerza, 211 s Belkhova R.K., 211

3 1. Razširitev 2π-periodičnih funkcij na niz Fur'є Viznachennya. Dodelitev funkciji f (x) imenujemo funkcionalni niz a 2 + (an cosnx + bn sin nx), (1) funkcije an, bn se izračunajo po formulah: an = 1 π bn = 1 π f (x) cosnxdx, n =, 1, ..., (2) f (x) sin nxdx, n = 1, 2, .... (3) Formule (2) (3) se imenujejo Euler Fur'є formule. Dejstvo, da je funkcija f (x) podobna vrsti Fur'є (1), je zapisano v obliki f (x) a 2 + (an cosnx + bn sin nx) (4) in zdi se, da je desni del formulo (4) є s formalno vrsto Fur'є funkcije f (x). Z drugimi besedami, zdi se, da formula (4) pomeni, da učinkovitost a n, b n ni znana za formule (2), (3). 3

4 Viznachennya. 2π-periodična funkcija f (x) se imenuje shmatkovo-gladka, tudi če je v intervalu [, π] Kincevo število točk = x< x 1 <... < x n = π таких, что в каждом открытом промежутке (x j, x j+1) функция f(x) непрерывно дифференцируема, а в каждой точке x j существуют конечные пределы слева и справа: f(x j) = lim h + f(x j h), f(x j +) = lim h + f(x j + h), (5) f(x j h) f(x j) f(x j + h) f(x j +) lim, lim. h + h h + h (6) Отметим, что последние два предела превратятся в односторонние производные после замены предельных значений f(x j) и f(x j +) значениями f(x j). Теорема о представимости кусочно-гладкой функции в точке своим рядом Фурье (теорема о поточечной сходимости). Ряд Фурье кусочно-гладкой 2π-периодической функции f(x) сходится в каждой точке x R, а его сумма равна числу f(x), если x точка непрерывности функции f(x), f(x +) + f(x) и равна числу, если x точка разрыва 2 функции f(x). ПРИМЕР 1. Нарисуем график, найдем ряд Фурье функции, заданной на промежутке [, π] формулой, f(x) = x, предполагая, что она имеет период 2π, и вычислим суммы 1 1 числовых рядов (2n + 1) 2, n 2. n= Решение. Построим график функции f(x). Получим кусочно-линейную непрерывную кривую с изломами в точках x = πk, k целое число (рис. 1). 4

5 Majhna. 1. Graf funkcije f (x) Izračunljiva učinkovitost Fur'є a = 1 π f (x) dx = 1 π x 2 2 π = π, an = 1 π f (x) cosnxdx = 2 π = 2 () x sin nx cos nx + π nn 2 = 2 π (1) n 1 n 2 = bn = 1 π π = 2 π f (x) cosnxdx = cos nx cos n 2 = 4 πn2, za n neparnih, za n seznanjenih, f (x) sin nxdx =, zato je funkcija f (x) seznanjena. Za funkcijo f (x) lahko zapišemo formalno Fur'є vrsto: f (x) π 2 4 π k = 5 cos (2k + 1) x (2k + 1) 2.

6 Jasno je, da je funkcija f (x) kosično gladka. Ker je torej brez prekinitve, se šteje le med (6) na končnih točkah med x = ± π in na točki zla x =: í f (π h) f (π) π h π f (+ h ) f (+) + h () lim = lim h + hh + hf (+ h) f (+) + h lim = lim = 1, h + hh + h = 1, f (h) f () h ( ) lim = lim = 1. h + hh + h Med іsnyu in іntsevі, čeprav je funkcija bolj gladka. Po izreku o krapkovu se vrednost Fuhrove serije na točkah kože konvergira k f (x), tako da je f (x) = π 2 4 π k = cos (2k + 1) + x (2k + 1) 2 = = π 2 4 (cosx + 19 π cos 3x) cos 5x (7) Na sl. 2, 3 označuje naravo približevanja delnih vsot nizu Fur'є S n (x), de S n (x) = an 2 + (ak coskx + bk sin kx), k = 1 funkciji f (x) v intervalu [, π]. 6

7 Majhna. 2. Graf funkcije f (x) z namestitvijo delnih vsot na grafih S (x) = a 2 in S 1 (x) = a 2 + a 1 cos x Sl. 3. Graf funkcije f (x) se naloži na nov graf vsote grafov S 99 (x) = a 2 + a 1 cos x + + a 99 cos 99x 7

8 Če oddamo v (7) x = otrimaєmo: = π 2 4 π k = 1 (2k + 1) 2, zvezde poznajo vsoto številčnega niza: = π2 8. Če poznamo vsoto vrstice, je enostavno poznamo naslednjo vsoto Maєmo: S = ( ) S = () = π S, celo S = π2 6, torej 1 n = π Vsota slavne serije prvega znanega Leonarda Eilerja. Vona se pogosto uči matematične analize in dodatkov. PRILOGA 2. Na majhnem grafu poznamo vrsto Funkcij, podano s formulo f (x) = x za x< π, предполагая, что она имеет период 2π, и вычислим суммы числовых (1) n) рядов + n= ((2n + 1,) (k k + 1) Решение. График функции f(x) приведен на рис. 4. 8

9 Majhna. 4. Graf funkcije f (x) Funkcijo f (x) kontinuirano diferencira interval (, π). V točkah x = ± π je med (5) več točk: f () =, f (π) = π. Poleg tega obstaja razlika med (6): f (+ h) f (+) lim = 1 і h + hf (π h) f (π +) lim = 1. h + h gladka funkcija. Če je funkcija f (x) neparna, potem je a n =. Znano je, da je zmogljivost bn integrirana po delih: bn = 1 π f (x) sin πnxdx = 1 [x cosnx π πn + 1 n = 1 πn [(1) n π + (1) n π] = 2 ( 1) n + 1. n Zelo formalna serija Fur'є funkcij 2 (1) n + 1 f (x) sin nx. n 9 cosnxdx] =

10 V skladu z izrekom o toku, vrednosti krčljivo gladke 2π-periodične funkcije, se serija Fur funkcije f (x) spusti na vsoto: 2 (1) n + 1 sin nx = nf (x) = x, kot π< x < π, = f(π) + f(π +) 2 =, если x = π, (8) f() + f(+) =, если x =. 2 На рис. 5 8 показан характер приближения частичных сумм S n (x) ряда Фурье к функции f(x). Рис. 5. График функции f(x) с наложенным на него графиком частичной суммы S 1 (x) = a 2 + a 1 cos x 1

11 Majhna. 6. Graf funkcije f (x) bo prekrit na graf vsote grafa S2 (x) Sl. 7. Graf funkcije f (x) prekrit z novim grafom vsote grafov S 3 (x) 11

12 Majhna. 8. Graf funkcije f (x) bo naložen na nov graf vsote S 99 (x). Zanesljivo (8) x = π / 2. Todi 2 () + ... = π 2, ali = n = (1) n 2n + 1 = π 4. Z lahkoto smo poznali vsoto družine Leibniz. Če imamo poklavl v (8) x = π / 3, vemo () + ... = π 2 3 ali (1+ 1) () (k) 3π + ... = 3k

13 PRILOGA 3. Majhen graf, poznamo vrsto Fur'є funkcij f (x) = sin x, pri čemer priznavamo, da je obdobje 2π, і 1 se izračuna kot vsota številskega niza 4n 2 1. Rešitev. Graf funkcije f (x) je prikazan na sl. 9. Očitno je f (x) = sin x neprekinjena parna funkcija iz obdobja π. Ale 2π je tudi obdobje funkcije f (x). Majhna. 9. Graf funkcije f (x) Izračunljiva učinkovitost Fur'є. Usi b n = na dejstvo, da je funkcija seznanjena. Okronan s trigonometričnimi formulami, je oštevilčen an pri n 1: an = 1 π = 1 π sin x cosnxdx = 2 π sin x cosnxdx = (sin (1 + n) x sin (1 n) x) dx = = 1 ( ) π cos (1 + n) x cos (1 n) x + = 2 () 1 + (1) n = π 1 + n 1 n π 1 n 2 (4 1, ko je n = 2k, = π n 2 1, ko je n = 2k

14 Izračun nam ne omogoča, da poznamo koeficient a 1, zato se pri n = 1 imenovalec ponastavi na nič. K temu se izračuna koeficient a 1 brez sredine: a 1 = 1 π sin x cosxdx =. Torej, ker je f (x) neprekinjeno diferenciran na (,) і (, π) і v točkah kπ, (k je število), če je točka med (5) in (6), potem serija Fur' ê funkcije ne konvergirajo v točko kože: = 2 π 4 π sinx = 2 π 4 π cos 2nx 4n 2 1 = (1 1 cos 2x cos 4x + 1) cos 6x Sl. 1. Graf funkcije f (x) se naloži na graf vsote preseka S (x) 14

15 Majhna. 11. Graf funkcije f (x) prekrit na novem grafu vsote preseka S1 (x) Sl. 12. Graf funkcije f (x) bo naložen na nov graf vsote grafov S2 (x) Sl. 13. Graf funkcije f (x) prekrit z novim grafom vsote grafov S 99 (x) 15

16 1 Izračunljiva vsota številske vrstice. Za celoten 4n 2 1 je zadovoljivo (9) x =. Todi cosnx = 1 za vse n = 1, 2, ... i Otzhe, 2 π 4 π 1 4n 2 1 =. 1 4n 2 1 = = 1 2. APLIKACIJA 4. Verjetno, da je funkcija f (x) gladka in brez prekinitev, sem zadovoljen s f (x π) = f (x) za vse x (torej je π -periodično), a 2n 1 = b 2n 1 = za vse n 1 in navpaki, če je a 2n 1 = b 2n 1 = za vse n 1, potem je f (x) π-periodična. Odločitev. Naj bo funkcija f (x) π-periodična. Izračunljiva njena učinkovitost Fur'є a 2n 1 і b 2n 1: = 1 π (a 2n 1 = 1 π f (x) cos (2n 1) xdx + f (x) cos (2n 1) xdx =) f (x ) cos (2n 1) xdx. Pri prvem integralu zlahka zamenjam spremembo x = t π: f (x) cos (2n 1) xdx = f (t π) cos (2n 1) (t + π) dt. 16

17 Klovn, cos (2n 1) (t + π) = cos (2n 1) t і f (t π) = f (t), lahko vidimo: a 2n 1 = 1 π (f (x) cos (2n 1) x dx +) f (x) cos (2n 1) x dx =. Podobno je treba narediti, b 2n 1 =. Nawpaki, naj a 2n 1 = b 2n 1 =. Ker je funkcija f (x) brez prekinitve, je v skladu z izrekom manifestacija funkcije na točkah njene serije F (x π) = f (x) = (a 2n cos 2nx + b 2n sin 2nx). (a2n cos 2n (x π) + b 2n sin 2n (x π)) = (a2n cos 2nx + b 2n sin 2nx) = f (x), kar pomeni, da je f (x) π-periodična funkcija. DODATEK 5. Lahko rečemo, da je funkcija f (x) gladka in gladka, f (x) = f (x) za vse x, nato a = í a 2n = b 2n = za vse n 1, in navpaki, npr. a = a 2n = b 2n =, potem f (x π) = f (x) vsi x. Odločitev. Naj bo funkcija f (x) zadovoljna s f (xπ) = f (x). Številni njeni kofіtsієnti Fur'є: 17

18 = 1 π (a n = 1 π f (x) cos nxdx + f (x) cosnxdx =) f (x) cosnxdx. Pri prvi integraciji bom enostavno zamenjal spremembo x = t π. Todi f (x) cosnxdx = f (t π) cosn (t π) dt. Crimson tim, cos n (t π) = (1) n cosnt in f (t π) = f (t), lahko sprejmemo: an = 1 π ((1) n) f (t) cosnt dt =, če n seznanjeno = 2 π f (t) cos nt dt, ko je n neparno. π Podobno se naredi, b 2n =. Nawpaki, naj a = a 2n = b 2n =, za vse n 1. Ker je funkcija f (x) brez prekinitve, potem velja izrek o eksplicitnosti funkcije v točkah njene serije Fur'є, da je f (x ) = (a 2n 1 cos (2n 1) x + b 2n 1 sin (2n 1) x). osemnajst

19 Todi = f (x π) = = = f (x). DODATEK 6. Vivchimo yak poleg še naprej integriran na vrzel [, π / 2] s funkcijo f (x) na vrzel [, π], tako da je vrstica Fur'є mav viglyad: a 2n 1 cos ( 2n 1) x. (1) Odločba. Naj bo graf funkcije ma viglyada, ki lebdi na sl. 14. Nihanja v vrstici (1) a = a 2n = b 2n = za vse n, potem je zadnjica 5 vyplyaє, vendar je funkcija f (x) kriva za enako pariteto f (xπ) = f (x) za vse x. Obstaja način za izboljšanje funkcije f (x) med [, / 2]: f (x) = f (x + π), sl. 15. Poleg tega je vrstica (1) namenjena maščevanju samo kosinusom, je urejena, vendar se funkcija f (x) nadaljuje kot par (to je, da je graf simetričen na os Oy), riž

20 Majhna. 14. Graf funkcije f (x) Majhna. 15. Graf nastavljene funkcije f (x) za napredek [, / 2] 2

21 Otzhe, funkcija ma viglyada, vodenje na sl. 16. Majhna. 16. Graf nadaljevanja funkcije f (x) za napredek [, π] [π / 2, π], graf funkcije f (x) je centralno simetričen na točko (π / 2,), in intervalu [, π] je graf simetričen na os Oy. 21

22 REFERENČNE APLIKACIJE 3 6 Nekhai l>. Očitno dva uma: a) f (l x) = f (x); b) f (l + x) = f (x), x [, l / 2]. Z geometrijskega vidika točka (a) pomeni, da je graf funkcije f (x) simetričen vzdolž navpične premice x = l / 2, graf (b), kjer je graf f (x) središčno simetrično glede na točko (l / 2;) na osi abscis. Velja naslednje: 1) če je funkcija f (x) seznanjena z Viconan Umov (a), potem b 1 = b 2 = b 3 = ... =, a 1 = a 3 = a 5 = ... =; 2) če je funkcija f (x) seznanjena z Viconan Umov (b), potem b 1 = b 2 = b 3 = ... =, a = a 2 = a 4 = ... =; 3) če je funkcija f (x) neparna in Viconan Umov (a), potem a = a 1 = a 2 = ... =, b 2 = b 4 = b 6 = ... =; 4) če je funkcija f (x) neparna in Viconan Umov (b), potem a = a 1 = a 2 = ... =, b 1 = b 3 = b 5 = ... =. ZAVDANNA Za naloge 1 7 pobarvaj grafe in pozna serijo Fur'є za funkcije,< x <, 1. f(x) = 1, если < x < π. 1, если < x < /2, 2. f(x) =, если /2 < x < π/2, 1, если π/2 < x < π. 3. f(x) = x 2 (< x < π). 4. f(x) = x 3 (< x < π). { π/2 + x, если < x <, 5. f(x) = π/2 x, если < x < π. 22

23 (1, jakšo / 2< x < π/2, 6. f(x) = 1, если π/2 < x < 3π/2. {, если < x <, 7. f(x) = sin x, если < x < π. 8. Как следует продолжить интегрируемую на промежутке [, π/2] функцию f(x) на промежуток [, π], чтобы ее ряд Фурье имел вид: b 2n 1 sin (2n 1)x? Ответы sin(2n 1)x sin(2n + 1)x. π 2n 1 π 2n + 1 n= 3. 1 (1) n () 12 3 π2 + 4 cosnx. 4. (1) n n 2 n 2π2 sin nx. 3 n 5. 4 cos(2n + 1)x π (2n + 1) (1) n cos(2n + 1)x. π 2n + 1 n= n= 7. 1 π sin x 2 cos 2nx. 8. Функцию следует продолжить следующим образом: f(x) = f(x), f(π x) = f(x), π 4n 2 1 то есть на промежутке [, π], график функции f(x) будет симметричен относительно вертикальной прямой x = π/2, на промежутке [, π] ее график центрально симметричен относительно точки (,). 23

24 2. Razširitev funkcije, podane v intervalu [, π], samo po sinusih ali samo po kosinusih Funkcija f je podana v intervalu [, π]. V celotnem razponu bomo razširili prostor do Fur'є vrstice, lahko nadaljujemo s f na izboklini [, π] z višjim rangom, hkrati pa bo hitreje s formulami Eiler Fur' є. Svavilja pri napredni funkciji izdelati prej, za eno vrsto funkcije f: [, π] R lahko odstranimo številne Fur'є. Druga možnost je, da lahko vikoristovuvat tse svavillya tako, da samo obrezujete širitev samo za sinusi ali samo po kosinusih: prvi vipad ima dovolj za promocijo f z neparnim rangom in na drugačen način za fante. Algoritem rešitve 1. Nadaljujte funkcijo z neparnim (moškim) rangom (,) in nato periodično, vsakih 2π, nadaljujte funkcijo za celoto. 2. Izračunajte zmogljivost Fur'є. 3. Zložite serijo Fur funkcije f (x). 4. Revizijski umi so nizki. 5. Predstavite funkcijo, za katero je cela vrstica. DODATEK 7. Uporabljeno za funkcijo f (x) = cosx,< x < π, в ряд Фурье только по синусам. Решение. Продолжим функцию нечетным образом на (,) (т. е. так, чтобы равенство f(x) = f(x) выполнялось для всех x (, π)), а затем периодически с периодом 2π на всю ось. Получим функцию f (x), график которой приведен на рис

25 Majhna. 17. Graf nastavljene funkcije Očitno je funkcija f (x) sramežljivo gladka. Številni funkcionalni Fur'є: a n = vse n do te mere, da je funkcija f (x) neparna. Če je n 1, potem je bn = 2 π f (x) sin πnxdx = 2 π cosx sin nxdx = = 2 π dx = = 2 π cos (n + 1) x cos (n 1) x + = 1 = 1 (1 ) n (1) n 1 1 = π n + 1 n 1 = 1, kjer je n = 2 k + 1, (1) n + 1 (n 1) + (n + 1) = π (n + 1) ( n 1) 2 2n, kjer je n = 2k. π n 2 1 Ko je n = 1, se imenovalec obrne na nič na sprednji strani kalkulatorjev, zato se koeficient b 1 izračuna brez prejšnjih 25

26 spanje: b 1 = 2 π cosx sin xdx =. Niz funkcij Fur'є f (x) je zložljiv: f (x) 8 π k = 1 k 4k 2 1 sin 2kx. Če je funkcija f (x) sramežljivo gladka, potem po izreku o krapkovih vrednost serije Fur funkcije f (x) preide na sumi: cosx, kjer je π< x <, S(x) =, если x =, x = ±π, cosx, если < x < π. В результате функция f(x) = cosx, заданная на промежутке (, π), выражена через синусы: cosx = 8 π k=1 k 4k 2 1 sin 2kx, x (, π). Рис демонстрируют постепенное приближение частичных сумм S 1 (x), S 2 (x), S 3 (x) к разрывной функции f (x). 26

27 Majhna. Slika 18. Graf funkcije f (x), prekrit na novem grafu vsote kosov S1 (x) Sl. 19. Graf funkcije f (x), prekrit z novim grafom vsote grafov S 2 (x) 27

28 Majhna. 2. Graf funkcije f (x) bo naložen na graf presečne vsote S3 (x). 21 so prikazani grafi funkcije f (x) in delne vsote S 99 (x). Majhna. 21. Graf funkcije f (x), prekrit z novim grafom vsote grafov S 99 (x) 28

29 PRILOGA 8. Razširljivo s funkcijo f (x) = e ax, a>, x [, π], do niza Fur'є samo v kosinusih. Odločitev. Neprekinjeno s funkcijo ranga fanta (,) (tako da je pariteta f (x) = f (x) prikazana vsem x (, π)), se to občasno s periodo 2π razteza navzgor. . Lahko sprejmemo funkcijo f (x), graf takšnih predstavitev na sl. 22. Funkcija f (x) v točkah Mal. 22. Graf nastavljene funkcije f (x) x = kπ, k je celo število, tako kot olja. Številno kofіtsієnti Fur'є: b n =, oskіlki f (x) v paru. Integrirajte z deli Mo 29

30 an = 2 π a = 2 π = 2 cosnxd (e ax) = 2 πa e ax dx = 2 π a (eaπ 1), f (x) cos πnxdx = 2 π πa eax cosnx = 2 πa (eaπ cosnπ 1 ) + 2n πa 2 π e ax cos nxdx = + 2n e ax sin nxdx = πa sin nxde ax = = 2 π a (eaπ cos n π 1) + 2n π sin nx π a 2eax 2n2 e ax ax a (eaπ cos n π 1) n2 aa n. 2 Otzhe, a n = 2a e aπ cos n π 1. π a 2 + n 2 Nihanja f (x) so brez prekinitve, potem se po izreku o toku serija Fur konvergira k f (x). Prav tako vsi x [, π] maєmo f (x) = 1 π a (eaπ 1) + 2a π k = 1 e aπ (1) k 1 a 2 + k 2 coskx (x π). Riž prikazuje delovanje približevanja delnih vsot številu Fur'є dani funkciji rezanja. 3

31 Majhna. 23. Grafi funkcij f (x) in S (x) Mal. 24. Grafi funkcij f (x) in S1 (x) Majhna. 25. Grafi funkcij f (x) in S2 (x) Majhna. 26. Grafi funkcij f (x) in S 3 (x) 31

32 Majhna. 27. Grafi funkcij f (x) in S4 (x) Mal. 28. PREDSTAVLJENA grafa funkcij f (x) in S 99 (x) 9. Funkcijo f (x) = cos x, x π umestimo v vrsto Fur'є samo v kosinusih. 1. Funkcijo f (x) = e ax, a>, x π razširimo na vrstico Fur'є samo za sinusi. 11. Funkcijo f (x) = x 2, x π postavimo v vrstico Fur'є le za sinusi. 12. Določi funkcijo f (x) = sin ax, x π, y niz Fur'є samo v kosinusih. 13. Funkcijo f (x) = x sin x, x π postavimo v vrstico Fur'є le za sinusi. Vidpovidi 9.cosx = cosx. 1. e ax = 2 [1 (1) k e aπ] k sin kx. π a 2 + k2 k = 1 11. x 2 2 [π 2 (1) n 1 π n + 2] n 3 ((1) n 1) sin nx. 32

33 12. Če a ni celo število, sin ax = 1 cosaπ (1 + + 2a cos 2nx) + π a 2 (2n) 2 + 2a 1 + cosaπ cos (2n 1) x π a 2 (2n 1) 2 ; če je a = 2m par število, potem sin 2mx = 8m cos (2n 1) x π (2m) 2 (2n 1) 2; če je a = 2m 1 pozitivno neparno število, potem je sin (2m 1) x = 2 (cos 2nx) 1 + 2 (2m 1). π (2m 1) 2 (2n) π 16 n sin x sin 2nx. 2 π (4n 2 1) 2 3. Serija Fury funkcije z določeno periodo Recimo, da je funkcija f (x) nastavljena v intervalu [l, l], l>. Po zamenjavi x = ly, y π lahko izpeljemo funkcijo g (y) = f (ly / π), kar pomeni v intervalu π [, π]. Tretja funkcija g (y) tvori (formalno) serijo Fur'є () ly f = g (y) a π 2 + (an cosny + bn sin ny), katere učinkovitost je za formulo Euler Fur'є : an = 1 π g (y) cosny dy = 1 π f (ly π) cos ny dy, n =, 1, 2, ..., 33

34 bn = 1 π g (y) sinny dy = 1 π f () ly sin ny dy, n = 1, 2, .... π Za funkcijo f (x) lahko trigonometrično vrsto zlahka spremenimo v pogled: de f (x) a 2 + an = 1 lbn = 1 lllll sin πnx), (11) l dx, n =, 1, 2, ..., ( 12) dx, n = 1, 2, . .. DODATAK 9. Poznamo vrsto Fur'є funkcij, ki jih v intervalu (l, l) poda viraz (A, kjer je l< x, f(x) = B, если < x < l, считая, что она периодична с периодом 2l. Решение. Продолжим функцию периодически, с периодом 2l, на всю ось. Получим функцию f (x), кусочно-постоянную в промежутках (l + 2kl, l + 2kl), и претерпевающую разрывы первого рода в точках x = lk, k целое число. Ее коэффициенты Фурье вычисляются по формулам (12) и (13): 34

35 a = 1 llf (x) dx = 1 l A dx + 1 ll B dx = A + B, llan = 1 lllf (x) cos πnx l dx = = 1 l = 1 ll A cos πnx l = A + B π nlbn = 1 l dx + 1 ll B cos πnx l sin πn =, kjer je n, ll A sin πnx lf (x) sin πnx l dx + 1 ll dx = B sin πnx l = BA (1 cosπn). πn Serija Fur funkcije f (x) je zložljiva: f (x) A + B π (B A lestvice cosπn = (1) n, nato n dx = dx = (1 cosπn) sin πnx). l za n = 2k je mogoče zamisliti b n = b 2k =, za n = 2k 1 b n = b 2k 1 = 35 2 (BA) π (2k 1).

36 Zvezd f (x) A + B (BA)? yaksho l< x, S(x) = A + B, если x =, x = ±l, 2 B, если < x < l. Придавая параметрам l, A, B конкретные значения получим разложения в ряд Фурье различных функций. Пусть l = π, A =, B = 3π. На рис. 29 приведены графики первых пяти членов ряда, функции f (x) и частичной суммы S 7 (x) = a 2 + b 1 sin x b 7 sin 7x. Величина a является средним значением функции на промежутке. Обратим внимание на то, что с возрастанием ча- 2 стоты гармоники ее амплитуда уменьшается. Для наглядности графики трех высших гармоник сдвинуты по вертикали. На рис. 3 приведен график функции f(x) и частичной суммы S 99 (x) = a 2 + b 1 sin x b 99 sin 99x. Для наглядности на рис. 31 приведен тот же график в другом масштабе. Последние два графика иллюстрируют явление Гиббса. 36).

37 Majhna. 29. Graf funkcije f (x) s superponiranim na novih grafih harmonik S (x) = a 2 in S 1 (x) = b 1 sinx. Za specifičnost grafa treh drugih harmonikov S 3 (x) = b 3 sin 3πx, S l 5 (x) = b 5 sin 5πx l in S 7 (x) = b 7 sin 7πx potisk navpično navzgor l 37

38 Majhna. 3. Graf funkcije f (x) se naloži na nov graf vsote kosov S 99 (x) Sl. 31. Odlomek sl. 3 na lestvici 38

39 PROMOCIJA V problemih prostora v seriji Fur'є so funkcije dodeljene nalogam. 14.f (x) = x 1, (1, 1). 15.f (x) = ch2x, (2, 2] f (x) = x (1 x), (1, 1). 17.f (x) = cos π x, [1, 1] f (x ) = sin π x, (1, 1). (2 1, kjer je 1< x < 1, 19. f(x) = 2l = 4., если 1 < x < 3; x, если x 1, 2. f(x) = 1, если 1 < x < 2, 2l = 3. { 3 x, если 2 x < 3;, если ωx, 21. f(x) = 2l = 2π/ω. sin ωx, если ωx π; Разложить в ряды Фурье: а) только по косинусам; б) только по синусам указанные функции в заданных промежутках (, l) { 22. f(x) = { 23. f(x) = ax, если < x < l/2, a(l x), если l/2 < x < l. 1, если < x 1, 2 x, если 1 x 2. Ответы 14. f(x) = 4 cos(2n 1)πx. π 2 (2n 1) f(x) = sh sh4 (1) n nπx cos 16 + π 2 n f(x) = cos 2nπx. π 2 n f(x) = 2 π + 8 π (1) n n 1 4n 2 cosnπx. 39

40 18.f (x) = 8 (1) n n sin nπx. π 1 4n (1) n 2n + 1 cos πx. π 2n πn 2πnx π 2 sin2 cos n π sin ωx 2 cos 2nωx π 4n 2 1. (l 22. а) f (x) = α 2) l b) f (x) = 4al (1) n 1 (2n 1) ) πx sin. π 2 (2n 1) 2 l 23.a) f (x) = (cos π π 2 2 x 2 2 cos 2π 2 2 x cos 3π 2 2 x cos 5π), 2 2 x ... b) f ( x) = 4 (sin π π 2 2 x 1 3 sin 3π) + 2 2 x (sin π π 2 x cos 2π) 2 x Kompleksna oblika na vrsto Fur'є Porazdelitev f (x) = cne inx, de cn = 1 2π f (x) e inx dx, n = ± 1, ± 2, ..., bomo imenovali kompleksna oblika serije Fur'є. Funkcija zlaganja v zapleteno vrsto Fur'є z vizijo tihih umov, zaradi česar jih je mogoče umestiti v govorno vrsto Fur'є. 4

41 PRILOGA 1. Poznamo vrsto Fur kompleksne oblike funkcije, podane s formulo f (x) = e ax, y med [, π), de govorno število. Odločitev. Količinsko merljiva zmogljivost: = c n = 1 2π f (x) e inx dx = 1 2π e (a in) x dx = 1 ((1) n e aπ (1) n e aπ) = (1) n sh aπ. 2π (a in) π (a in) Kompleksni niz Fur funkcije f stroja f (x) sh aπ n = (1) n a in einx. Ponovno premislek, torej je funkcija f (x) grudasto gladka: v intervalu (, π) je neskončno diferencirana, v točkah x = ± π pa so točke med (5), (6) lim h + ea (+ h) = e aπ, lim h + ea (π h) = e aπ, ea (+ h) ea (+) lim h + h = ae aπ ea (π h) ea (π), lim h + h = ae aπ. Prav tako je funkcija f (x) predstavljena z vrstnim redom Fur'є sh aπ π n = (1) n a v einx, kar naj bi šlo na sumi: (e S (x) = ax, kjer je π< x < π, ch a, если x = ±π. 41

42 PRILOGA 11. Poznamo vrsto Fur za kompleksno in govorno obliko funkcije, podano s formulo f (x) = 1 a 2 1 2a cosx + a2, de a< 1, a R. Решение. Функция f(x) является четной, поэтому для всех n b n =, а a n = 2 π f(x) cosnxdx = 2 (1 a2) π cos nxdx 1 2a cosx + a 2. Не будем вычислять такой сложный интеграл, а применим следующий прием: 1. используя формулы Эйлера sin x = eix e ix 2i = z z 1, cosx = eix + e ix 2i 2 = z + z 1, 2 где z = e ix, преобразуем f(x) к рациональной функции комплексной переменной z; 2. полученную рациональную функцию разложим на простейшие дроби; 3. разложим простейшую дробь по формуле геометрической прогрессии; 4. упростим полученную формулу. Итак, по формулам Эйлера получаем = f(x) = 1 a 2 1 a(z + z 1) + a 2 = (a 2 1)z (z a)(z a 1) = a z a az. (14) 42

43 Nagadaєmo, vreča neskončnega geometrijskega napredka s standardnim q (q< 1) вычисляется по формуле: + n= q n = 1 1 q. Эта формула верна как для вещественных, так и для комплексных чисел. Поскольку az = a < 1 и a/z = a < 1, то az = + a n z n = a n e inx, a z a = a z 1 1 a/z = a z n= + n= a n z = + n n= n= a n+1 z = + a n+1 e i(n+1)x. n+1 После замены переменной (n + 1) = k, < k < 1, получим: 1 a z a = a k e ikx. Следовательно, f(x) + n= k= c n e inx, где c n = n= { a n, если n, a n, если n <, то есть c n = a n. Поскольку функция f(x) непрерывна, то в силу теоремы о поточечной сходимости имеет место равенство: f(x) = + n= a n e inx. Тем самым мы разложили функцию f(x) в ряд Фурье в комплексной форме. 43

44 Zdaj poznamo številne Fur'є v govornih oblikah. Za celotno skupino dopolnitev s številkama n in n za n: a n e inx + a n e inx = 2a neinx + e inx Oskilki c = 1, potem je 2 = 2a n cos nx. f (x) = 1 a 2 1 2a cosx + a = a n cosnx. 2 Niz Fur'є pri govorni obliki funkcije f (x). Ta rang, če ne štejemo ekonomskega integrala, smo poznali nizko funkcijo Fur'є. Ko virahuvali, je pomemben integral, ki ga najdemo v parametru cos nxdx 1 2a cosx + a = 2 π an 2 1 a2, a< 1. (15) ПРИМЕР 12. Найдем ряд Фурье в комплексной и вещественной форме функции, заданной формулой a sin x f(x) = 1 2a cosx + a2, a < 1, a R. Решение. Функция f(x) является нечетной, поэтому для всех n a n = и b n = 2 π f(x) sin nxdx = 2a π sin x sin nxdx 1 2a cosx + a 2. Чтобы записать ряд Фурье нужно вычислить сложные интегралы или воспользоваться приемом, описанным выше. Поступим вторым способом: 44

45 a (zz 1) f (x) = 2i (1 a (zz 1) + a 2) = i 2 + i (a + a 1) z 2 2 (za) (za 1) = = i 2 + i () a 2 za + a 1. za 1 Dermal iz preprostih ulomkov lahko razstavimo po formuli geometrijskega napredka: + aza = a 1 z 1 a = aanzzn, n = za 1 za = az = anz n. n = Popolnoma, fragmenti az = a / z = a< 1. Значит + ia n /2, если n <, f(x) c n e inx, где c n =, если n =, n= ia n /2, если n >, abo, krajše, c n = 1 2i a n sgnn. Tim sam, je znano več Fur'є v zapleteni obliki. Ko združimo seštevanja s številkama n in n, lahko sklepamo niz Fur'є funkcij v govorni obliki: = f (x) = + a sin x 1 2a cosx + a + 2 = an sin nx. Poznam v daljavi virahuvati žaljiv zgibni integral: sin x sin nxdx 1 2a cosx + a 2 = π an 1. (16) 45

46 ZAVDANNYA 24. Vikoristovuchi (15), izračunaj integral cos nxdx 1 2a cosx + a 2 za govore a, a> Vikoristovuchi (16), izračunaj integral sin x sin nxdx za govore a, a> a cosx + a2 V težavah Fur'є pri zapletenih oblikah za funkcije. 26.f (x) = sgn x, π< x < π. 27. f(x) = ln(1 2a cosx + a 2), a < 1. 1 a cosx 28. f(x) = 1 2a cosx + a2, a < Докажите, что функция f, определенная в промежутке [, π], вещественнозначна, если и только если коэффициенты c n ее комплексного ряда Фурье связаны соотношениями c n = c n, n =, ±1, ±2, Докажите, что функция f, определенная в промежутке [, π], является четной (т. е. удовлетворяет соотношению f(x) = f(x)), если и только если коэффициенты c n ее комплексного ряда Фурье связаны соотношениями c n = c n, n = ±1, ±2, Докажите, что функция f, определенная в промежутке [, π], является нечетной (т. е. удовлетворяет соотношению f(x) = f(x)), если и только если коэффициенты c n ее комплексного ряда Фурье связаны соотношениями c n = c n, n =, ±1, ±2,.... Ответы 1 2π 24. a n a π a n i + e 2inx, где подразумевается, что слагаемое, соответствующее n =, пропущено. π n n= a n n cosnx. 28. a n cosnx. n= 46

47 5. Izrek o enakosti Ljapunova (Enakost Lyapunova). Naj bo funkcija f: [, π] R taka, da je f 2 (x) dx< +, и пусть a n, b n ее коэффициенты Фурье. Тогда справедливо равенство, a (a 2 n + b2 n) = 1 π называемое равенством Ляпунова. f 2 (x) dx, ПРИМЕР 13. Напишем равенство Ляпунова для функции { 1, если x < a, f(x) =, если a < x < π и найдем с его помощью суммы числовых рядов + sin 2 na n 2 и + Решение. Очевидно, 1 (2n 1) 2. 1 π f 2 (x) dx = 1 π a a dx = 2a π. Так как f(x) четная функция, то для всех n имеем b n =, a = 2 π f(x) dx = 2 π a dx = 2a π, 47

48 a n = 2 π f (x) cosnxdx = 2 π a cos nxdx = 2 sin na πn. Zato Ljapunovska ekvivalentnost za funkcijo f (x) nabrekne na oko: 2 a 2 π + 4 sin 2 na = 2a 2 π 2 n 2 π. Preostala enakovrednost za π je znana sin 2 na n 2 = a (π a) 2 Vazayuchy a = π 2, lahko vzamemo sin2 na = 1 za n = 2k 1 in sin 2 na = za n = 2k. Otzhe, k = 1 1 (2k 1) 2 = = π2 8. PRILOGA 14. Zapišemo Ljapunovsko enakost za funkcijo f (x) = x cosx, x [, π], í poznamo dodatno vsoto številski niz (4n 2 + 1) 2 (4n 2 1) 4.1 π Rešitev. Neposredni izračun daje = ππ f 2 (x) dx = 1 π x 2 cos 2 xdx = 1 π x sin 2xdx = π π x cos x = π x 21 + cos 2x dx = 2 π 1 4π cos 2xdx =

49 Oskilki f (x) je parna funkcija, potem je za vse n maєmo bn =, an = 2 π = 1 π 1 = π (n + 1) = f (x) cosnxdx = 2 π 1 cos (n + 1) x π (n + 1) 2 x cosxcosnxdx = x (cos (n + 1) x + cos (n 1) x) dx = 1 π sin (n + 1) xdx sin (n 1) xdx = π (n 1 ) π π 1 + cos (n 1) x = π (n 1) 2 1 (= (1) (n + 1) 1) 1 (+ (1) (n + 1) 1) = π (n + 1 ) 2 π (n 1) 2 () = (1) (n + 1) 1 1 π (n + 1) + 1 = 2 (n 1) 2 = 2 (1) (n + 1) 1 nk π ( n 2 1) = π (4k 2 1) 2, če je n = 2k, 2, če je n = 2k + 1. Vrednost a 1 je treba prešteti ločeno, fragmente v pripravljeni formuli za n = 1, se imenovalec ulomka obrne na nič. = 1 π a 1 = 2 π f (x) cosxdx = 2 π x (1 + cos 2x) dx = π 2 1 2π 49 x cos 2 xdx = sin 2xdx = π 2.

50 Tako je pariteta Lyapunova za funkcijo f (x) maviglyad: 8 π + π (4n 2 + 1) 2 π 2 (4n 2 1) = π, 2 1) = π π PREDSTAVITEV 32. Napišite enakovrednost Lyapunova za funkcija (xf (x) = 2 πx, kjer je x< π, x 2 πx, если π < x. 33. Напишите равенства Ляпунова для функций f(x) = cos ax и g(x) = sin ax, x [, π]. 34. Используя результат предыдущей задачи и предполагая, что a не является целым числом, выведите следующие классические разложения функций πctgaπ и (π/ sin aπ) 2 по рациональным функциям: πctgaπ = 1 a + + 2a a 2 n 2, (π) = sin aπ (a n) 2. n= 35. Выведите комплексную форму обобщенного равенства Ляпунова. 36. Покажите, что комплексная форма равенства Ляпунова справедлива не только для вещественнозначных функций, но и для комплекснозначных функций. 5

51 π (2n + 1) = π sin 2απ 2απ = 2sin2 απ α 2 π 2 Odgovori + 4 sin2 απ π 2 α 2 (α 2 n 2) 2; sin 2απ 1 2απ = απ n 2 4sin2 π 2 (α 2 n 2) 2,1 π 35. f (x) g (x) dx = cndn, de cn funkcija f (x) in dn Funkcijska funkcija g (x) . 6. Diferenciacija serije Fur'є Nekhai f: R R kontinuirano diferencirana 2π-periodična funkcija. Njena serija Fur'є ma viglyad: f (x) = a 2 + (n cos nx + b n sin nx). Podobno kot f (x) bo osrednja funkcija intermitentna 2π-periodična funkcija, za katero lahko zapišemo formalno vrsto Fur'є: f (x) a 2 + (an cos nx + bn sin nx), de a , an, bn, n = 1, 2, ... funkcionalnost Fur'є funkcija f (x). 51

52 Izrek (razširjena diferenciacija serije Fur). V primeru razpadajočega pripushennya je res, da je a =, an = nb n, bn = na n, n 1. APLIKACIJA 15. Ne bodi sramežljivo gladka funkcija f (x) brez prekinitve v intervalu [, π] . Očitno lahko rečemo, da je f (x) dx = majhno napačno vedenje 2 dx 2 dx, zaradi Steklove nezmožnosti in ponovne povezave, tako da bodo nove funkcije izgubile funkcijo f (x) tipa f (x) Z drugimi besedami, Steklova nesposobnost, recimo, ko vidite, da so tri preproste funkcije (v srednjem kvadratu), so tri funkcije (v srednjem kvadratu). Odločitev. Podprto s funkcijo f (x) do intervala [,] z rangom fanta. Znatno razširjeno s samo funkcijo s simbolom f (x). Funkcija se bo nadaljevala brez prekinitve in bo gladka in gladka na poti [, π]. Torej, ker je funkcija f (x) neprekinjena, je f 2 (x) neprekinjena ves čas in 2 dx< +, следовательно, можно применить теорему Ляпунова, согласно которой имеет место равенство 1 π 2 dx = a () a 2 n + b 2 n. 52

53 Oskіlki funkcija para se nadaljuje, potem b n =, a = za umivalnikom. Otzhe, pariteto Lyapunov nabuvє na oko 1 π 2 dx = a 2 π n. (17) Ponovno premislek, da se f (x) drži izrekov o diferenciaciji serije Fur'є, tako da je a =, an = nb n, bn = na n, n 1. Ne želim f (x) biti slab v točkah x 1, x 2, ..., x N v intervalu [, π]. Naj bo x = x N + 1 = π. Rast integracije [, π] na intervalu N +1 (x, x 1), ..., (x N, x N + 1), stanje kože f (x) je popolnoma diferencirano. Todi, začarana moč aditivnosti integrala in tudi integrirnih delov je prepoznavna: bn = 1 π = 1 π = 1 π f (x) sin nxdx = 1π j = xj + 1 xjx j + 1 xjnn π N j = xj + 1 xjx j + 1 xjf (x) sin nxdx = f (x) cosnxdx = f (x) cosnxdx = = 1 π [(f (x (x) 1) sin nx 1 f (x) sin nx) + + (f ( x 2) sinnx 2 f (x 1) sin nx 1)

54 + (f (x N + 1) sin nx N + 1 f (x N) sin nx N)] n = = 1 π na n = = 1 π na n = na n. x j + 1 a = 1 f (x) dx = 1 N f (x) dx = π π j = xj = 1 N x j + 1 f (x) π = 1 (f (π) f ()) = .. . x j π j = Ostajajo enaki drug drugemu skozi tiste, pri katerih je bila funkcija f (x) pospešena s tipovim rangom, in zato f (π) = f (). Podobno lahko prepoznamo an = nbn. Pokazali smo, da je izrek razširjene diferenciacije serije Fur'є za neprekinjeno shmatkovo-gladko 2π-periodično funkcijo, podobno kot pri vmesnem [, π], aroganten v prvi vrsti, vyrna. Iz istega f (x) a 2 + (an cosnx + bn sin nx) = (na n) sin nx, oskilki a =, an = nb n =, bn = na n, n = 1, 2, ... Oskilki 2 dx< +, то по равенству Ляпунова 1 π 2 dx = 54 n 2 a 2 n. (18)

55 Torej je kot kožni izraz v vrsti (18) bolj ali manj dodatni člen v vrstici (17), nato 2 dx 2 dx. Ugibam, scho f (x) є fantom v naprednih funkcijah, maєmo 2 dx 2 dx. Da prinesem Steklovo pariteto. Dandanes je v Steklovih nepravilnostih veliko funkcij. Če želite za en n 2 učinkovitost a n kot rezultat nič, potem a 2 n< na 2 n. Следовательно, равенство a 2 n = n 2 a 2 n возможно только если a n = для n 2. При этом a 1 = A может быть произвольным. Значит в неравенстве Стеклова равенство достигается только на функциях вида f(x) = A cosx. Отметим, что условие πa = f(x)dx = (19) существенно для выполнения неравенства Стеклова, ведь если условие (19) нарушено, то неравенство примет вид: a a 2 n n 2 a 2 n, а это не может быть верно при произвольном a. 55

56 POMOČ 37. Ne bodi sramežljiva funkcija f (x) je neprekinjena v intervalu [, π]. Obvestite, da morate, ko zmagate, f () = f (π) = majhna napaka 2 dx 2 dx, saj se temu reče tudi Steklova nesposobnost, in prestopite, vendar ni nič proti f (x) . .. 38. Naj bo funkcija f brez prekinitve v intervalu [, π] in v novem (za vinjeto neskončnega števila točk) bom šel f (x), tako da se integriramo s kvadratom. Če ob določeni viziji menite, da je f () = f (π) і f (x) dx =, potem malo manjka neučinkovitosti 2 dx 2 dx, kot se imenuje Wirtingerjeva neodločnost, funkcija pa je ni zelo preprosto za x) = A cosx + B sin x. 56

57 7. Stagnacija vrst Fur'є o pojavu diferencialnih ras med zasebnimi pokojniki Ko je oživitev resničnega predmeta (manifestacija narave, virusni proces, nadzorni sistem pretanek.) korak k razvoju . matematični aparat. Na stopnji znanstvenih študij se je taka sulica zamajala: fizični model je matematični model. Fizična formulacija (model) polja v ofenzivi je: pojavi se in razvije proces tistega glavnega faktorja, ki se prelije na novega. Matematična formulacija (model) polja v inventarju fizične formulacije faktorjev in umov v pogledu sistemov in enakih (algebraičnih, diferencialnih, integralnih itd.). Državni poglavar se imenuje pravilna nastavitev, saj v pevskem funkcionalnem prostoru reševanja miselnih nalog eno in edino in brez prekinitve polaga na storž in mejo umov. Matematični model ni le isti predmet, ki ga je treba pogledati, ampak se mu bomo približali z opisom. Viznovok pivnyannya vilnykh malikh prečne strune. Naj bodo vrvice pritrjene, sama vrvica pa napeta. Če vrvico vstavite s položaja ravne črte (na primer jo potegnete ven ali potegnete vzdolž), je verjetneje, da bo vrvica 57

58 vagatisya. Hkrati se vse točke strune zrušijo pravokotno na položaj ravnove (prečna povezava), poleg tega v trenutku kože struna leži na enem in istem območju. Obstaja pravokoten koordinatni sistem xou. Todi, če je v trenutku storža ob uri t = struna zrasla v os Ox, potem pomeni u sprostitev strune iz položaja premice, tako da je položaj točke strune od abscisa x v končnem trenutku ure t funkcije, tіє ​​vrednost Pri fiksni vrednosti t graf funkcije u (x, t) predstavlja obliko strune, ki jo lahko zavrtimo v času t (slika 32). S konstantno vrednostjo x daje funkcija u (x, t) zakon do točke abscise x, črta je ravna, vzporedna z osjo Ou, t se izgubi, druga pa se izgubi 2 ut 2 je pospešena . Majhna. 32. Sila, uporabljena na neomejeno majhno število nizov Skladišče, ki zadostuje za izpolnitev funkcije u (x, t). Za cel kup brutalnih posipov naj odpustijo. Vrvica je popolnoma napeta - 58

59 Coy, tako vvazhatimo, zakaj ne bi se struna zvila od viginu; tse pomeni, scho vzmeti, scho pomežika strunam, vedno zravnane glede na popolnoma enak njen profil rokavic. Struna se prenaša z vzmetjo in po Hookeovem zakonu; tse pomeni, da je bila sprememba velikosti povlečena sorazmerno s kačo strune. Sprejemljivo, enoverižna vrvica; tse pomeni, її її linea gustina ρ postіyna. Prebujajoče se sile so nezdrave. Tse označuje, kako ga lahko vidimo. Mi vivchatimo zakup strune so majhne. Če s ϕ (x, t) označimo rez med absciso in pikčasto črto na točki abscise x v trenutku t, potem je um otrokovega polja v tem, da je vrednost ϕ 2 (x , t) ni mogoče zlahka x, t), tako da je ϕ 2. Ker je kut ϕ malij, potem je tudi cos ϕ 1, ϕ sin ϕ tan ϕ і, lahko tudi vrednost (uxx,) 2 izpustimo. Sliši se naenkrat viplivay, toda v procesu petja lahko zehtuvati s kačo, tudi če ste ločevalec strun. Pravzaprav je treba na abscisni osi oblikovati malo vrvice M 1 M 2, de x 2 = x 1 + x, cesta l = x 2 x () 2 u dx x. x Pokazalo se bo, da bo za naše dodatke vrednost natezne sile T konstantna napetost strune. Hkrati želim prvič dilyanka strune M 1 M 2 (slika 32) ob uri t in namesto sodelovanja - 59

60 kv z vlečnimi silami T 1 in T 2. Nihanja za odtok vseh točk strune se zrušijo vzporedno z osjo Ou in navzven sil, potem je vsota projekcije vlečnih sil na os Ox odgovorna za nič: T 1 cosϕ (2 x 1, t) + (x 2, t) =. Začne se skozi majhno število kutiv ϕ 1 = ϕ (x 1, t) і ϕ 2 = ϕ (x 2, t) strukture, vendar T 1 = T 2. Pomembno je, da je začetna vrednost T 1 = T 2 do T. Zdaj vsota projekcij F u qix sil na os Ou: F u = T sin ϕ (x 2, t) T sin ϕ (x 1, t). (2) Oskіlki za majhne kutіv sin ϕ (x, t) tg? T (tan ϕ (x 2, t) tan ϕ (x 1, t)) (u T x (x 2, t) u) x (x 1, t) xx T 2 ux 2 (x 1, t) x ... Če je točka x 1 obrnjena, potem je F u T 2 u x2 (x, t) x. Poleg tega, ker je znano, da vse sile gredo na M 1 M 2, obstaja še en Newtonov zakon, kar pomeni, da je treba zagotoviti hitro oskrbo vseh sil dneva. Masa strune je M 1 M 2 za cesto m = ρ l ρ x, za pospešeno cesto pa 2 u (x, t). Enakovredno Newtonovemu t 2 s stališča: 2 u t (x, t) x = u 2 α2 2 x2 (x, t) x, de α 2 = T ρ je trajno pozitivno število. 6

61 Speedy na x, lahko definiramo mo 2 u t (x, t) = u 2 α2 2 x2 (x, t). (21) Posledično smo prikazali linearne razlike med zasebnimi, različnih velikosti, z zastarelo uspešnostjo. Yogo imenuje chi strune v isto vrsto kot iste. Rivnyannya (21) je preoblikoval Newtonov zakon in opisal propad strune. Ale pri fizičnem uprizoritvi balinanja vimogi o tistih strunah, ki se pripnejo in strune dajo v naslednji uri. Enakovredno zapišite takole: a) pomembno je, da je konec strun fiksiran na točkah x = і x = l, tako da je pomembno, za vse t visonov izvedbe u (, t) =, u (l, t) =, u (l, (22) b) pozorno, v trenutku t = je položaj niza postavljen pod graf funkcije f (x), tako da je za vse x [, l] enakovrednost u (x,) = f (x); (23) c) No, v času ure t = točka strune iz abscise x je podana hitrost g (x), torej tudi u (x,) = g (x). (24) t Spіvdnoshennya (22) se imenujejo mejni umi, spіvіdnoshennya (23) in (24) pa se imenujejo storžni umi. Matematični model prečnega vilnyh malikh 61

62 nizanje strun v dejstvu, da je treba narediti vrvico strun (21) z mejnimi umivalniki (22) in ponori (23) in (24) Odločitev vilnega majhnega prečnega nizanja strun po Fur' 'Roving po regiji (21) xl,< t <, удовлетворяющие граничным условиям (22) и начальным условиям (23) и (24), будем искать методом Фурье (называемым также методом разделения переменных). Метод Фурье состоит в том, что частные решения ищутся в виде произведения двух функций, одна из которых зависит только от x, а другая только от t. То есть мы ищем решения уравнения (21), которые имеют специальный вид: u(x, t) = X(x)T(t), (25) где X дважды непрерывно дифференцируемая функция от x на [, l], а T дважды непрерывно дифференцируемая функция от t, t >... Glede na (25) (21) lahko prepoznamo: X T = α 2 X T, (26) ali T (t) α 2 T (t) = X (x) X (x). (27) Zdi se, da so hudobni postali. Torej, če x і t ne leži eno smer od ena, potem levi del (27) ne leži okoli x, desni pa okoli t in povratna vrednost cich je približno 62

63 je lahko postopenjsko, kar je smiselno skozi λ: T (t) α 2 T (t) = X (x) X (x) = λ. Prepoznali bomo dva specifična diferencialna ekvivalenta: X (x) λx (x) =, (28) T (t) α 2 λt (t) =. (29) Za veliko mejo pomislimo (22), da vidimo X () T (t) = і X (l) T (t) =. Oskіlka smrad je mogoče videti vse t, t>, potem X () = X (l) =. (3) Poznamo odločitev rivnyannya (28), saj bi bila všeč mejnim umom (3). Vidni so trije pogledi. Vipadoc 1:>. Naj bo λ = β 2. Enakovredno (28) videzu X (x) β 2 X (x) =. Yogova značilnost je enaka k 2 β 2 = koren k = ± β. Otzhe, glava rešitve (28) ma viglyad X (x) = C e βx + De βx. Če ste krivi, da ste naredili napako, potem C in D tako, da je bil mejni odtok (3) ujet, tako da je X () = C + D =, X (l) = C e βl + De βl =. Оskіlki β, tsya sistem rіvnyan maє єdine raztopine C = D =. Otzhe, X (x) do 63

64 u (x, t). Tim sam je na vipadku 1 mi sprejel trivialno odločitev, kolikor ni bilo opaziti. Tip 2: λ =. Todi rіvnyannya (28) nabuvaє v pogledu X (x) = і th rešitev, očitno, je podana s formulo: X (x) = C x + d. Rešitev podamo na mejnem ponoru (3), lahko jo preberemo X () = D = і X (l) = Cl =, tudi C = D =. Iz istega časa sta X (x) in u (x, t), trivialno rešitev pa smo že zavrnili. Vipadoc 3: λ<. Обозначим λ = β 2. Уравнение (28) принимает вид: X (x)+β 2 X(x) =. Его характеристическое уравнение имеет вид k 2 + β 2 =, а k = ±βi являются его корнями. Следовательно, общее решение уравнения (28) в этом случае имеет вид X(x) = C sin βx + D cosβx. В силу граничных условий (3) имеем X() = D =, X(l) = C sin βl =. Поскольку мы ищем нетривиальные решения (т. е. такие, когда C и D не равны нулю одновременно), то из последнего равенства находим sin βl =, т. е. βl = nπ, n = ±1, ±2,..., n не равно нулю, так как сейчас мы рассматриваем случай 3, в котором β. Итак, если β = nπ (nπ) 2, l, т. е. λ = то существуют l решения X n (x) = C n sin πnx, (31) l C n произвольные постоянные, уравнения (28), не равные тождественно нулю. 64

65 Nadal nadavatimo n samo pozitivne vrednosti n = 1, 2, ..., fragmenti z negativnim n bodo odločitev o tem (kot pri nπ). πnx z najmočnejšimi funkcijami diferencialne enačbe (28) z regionalni umi (3). Zdaj je ohlapno povezan (29). Za novo značilnost ma viglyad k 2 α 2 λ =. (32) l 2 Oskіlki vishche mi s'yasuvali, vendar netrivialne rešitve X (x) іvnyannya (28) є, če je za negativno λ, enako λ = n2 π 2, potem enako λ mi in vidno daleč. Koren premice (32) ê k = ± iα λ, rešitev premice (29) pa je lahko videti takole: T n (t) = A n sin πnαt + B n cos πnαt, (33) ll de A n і B n najbolj vztrajen. Predstavljamo formuli (31) in (33) v (25), poznamo zasebno odločitev rivnyannya (21), vendar smo zadovoljni z regionalnimi umi (22): πnx. lll Vstavite množitelj C n na premcu і vstavite vrednost C n A n = bn in B n C n = an, napišite un (X, T) pri gledalcu (un (x, t) = an cos πnαt + bn sin πnαt ) sin πnx. (34) l l l 65

66 Vbodne vložke, ki prikazujejo rešitve u n (x, t), se imenujejo power string jigs. Oskilki rіvnyannya (21) in mejne zmage (22) lіnіynі in enosmerna, nato lіnіyna kombinacija rešitev (34) (u (x, t) = an cos πnαt + bn sin πnαt) sin πnx (35) lll dni ), ki zadovolji mejne ume (22) s posebno vibracijo izvedbe an i bn, ki bo zagotovila enako varnost števila. Danes je učinkovitost í bn raztopine (35) tako dobra, da ni bila le meja, ampak storž (23), da so (24), de f (x), g (x) dobili funkcijo (kjer f () = f (l) = g () = g (l) =). Impresivno je, da bosta funkciji f (x) in g (x) zadovoljili misli, ki bi jih razdelili na nizko Fur'є. Glede na (35) vrednost t = lahko vzamemo u (x,) = a n sin πnx l = f (x). Če diferenciramo vrsto (35) v t in predstavimo t =, lahko naredimo, da je ut (x,) = πnα bn sin πnx ll = g (x), funkciji širjenja f (x) in g (x) pa do Fur' je lava. Prav tako je a n = 2 l f (x) sin πnx l dx, b n = 2 l g (x) sin πnx dx. πnα l (36) 66

67 Ponudimo lahko različne možnosti za funkcionalnosti an in bn do števila (35), sprejemamo rešitev rivnyannya (21), pa tudi za mejne ume (22) in storževe (23) in ( 24). Tim smo se sami zavezali majhnim križnim strunam. Obstaja fizična sprememba funkcij moči u n (x, t) težav glede nizanja nizov, kot je podana s formulo (34). Prepisljivo її pri viglyadі de n (x, t) = n cos πnα l α n = a 2 n + b2 n, (t + δ n) sin πnx, (37) l πnα δ n = arctan b n. l a n Iz formule (37) je razvidno, da gredo vse točke strune harmonično z eno in isto frekvenco ω n = πnα in fazo πnα δ n. Amplituda strune, ki leži od l l abscisne x točke niza і ceste α n sin πnx. S takšnim številom vse točke vrvice takoj dosežejo največjo vidljivost v tej smeri in eno uro preidejo položaj črte. Te kolyvannya se imenujejo stoječe pohvale. Stoji za mate n + 1 nedestruktivno točko, kako vprašati korenine rivnyannya sin πnx = v intervalu [, l]. Neukrotljive točke se imenujejo vuze stoječih khvili. Na sredini vozlišč rastejo točke, v katerih pogledih dosežejo maksimum; take točke imenujemo antinode. Dermalno struno lahko uporabimo za striktno pojoče frekvence n = πnα, n = 1, 2, .... frekvence pa imenujemo močne frekvence strune. Najnižji ton l, ki ga lahko vidimo kot struno, se začne pri 67

68 frekvenca nizke moči 1 = π T і se imenuje osnovni ton strune. Drugi toni, ki ustrezajo l ρ frekvencam n, n = 2, 3, ..., se imenujejo prizvoni ali harmoniki. Za specifičnost vrste strun, vrsto glavnega tona (slika 33), prvega prizvoka (slika 34) in drugega prizvoka (slika 35). Majhna. 33. Profil strune, ki izgleda kot glavni ton Mal. 34. Profil strune, ki izgleda kot prvi prizvok. 35. Profil strune, ki je videti kot drugačen prizvok.Ko gre struna, se začne s storžnimi glavami, se pojavi funkcija u (x, t), kot je razvidno iz formul (35), v oči sumy je nekaj harmonik. Takšen čin zadostuje za kolonijo 68

69 strun je superpozicija stoječih kavljev. Hkrati je značaj zvoka strune (ton, moč zvoka, tember) v obliki sp_vdnoshennya med amplitudami harmonikov. Moč, višina in tember zvoka. Za moč zvoka je značilna energija zvoka. Zvok zvoka se začne s frekvenco obdobja chi: če je frekvenca višja, je zvok višji. Zvok zvoka se začne manifestirati v prizvokih, energija se dviga za harmonikami, tako da na način zvenenja tona. Amplitude prizvokov so očitno manjše od amplitude glavnega tona, faze prizvokov pa so lahko precej pomembne. Naš Vuho ni občutljiv na Phasie Kolivan. Primerjajte na primer dve krivulji na sl. 36, osumljen z. Tse posnamejo zvok z zelo osnovnim tonom, zvitim iz klarineta (a) in klavirja (b). Žaljivi zvoki niso preprosti sinusni zvoki. Osnovna frekvenca zvoka pri obeh vrstah je enaka in enak je ton. Malo krivulj glede dejstva, da se na glavni ton uporabljajo prizvoki. V pevskem smislu otroka pokažite isti tember. 69

Enakovredno hiperboličnemu tipu. Stolpec neinhibiranih in nedokončanih strun. Krzna metoda Krzna metoda Stoječi čvili 4 Predavanja 4.1. Enakovredno hiperboličnemu tipu. Zbirka ni neskončna in tako naprej.

MOSKVA DRŽAVNA TEHNIČNA UNIVERZA CIVILNEGA AVIATSIN V.M. Lyubimov, Є.A. Žukova, V.A. Ukhova, Yu.A. Šurinov M A T E M A T І K A R A D I POSIBNIK

MINISTRSTVO RUSKOG ZVEZNEGA državnega proračuna za izobraževanje Ustanova strokovnega izobraževanja MATI Ruska državna tehnološka univerza po K.E. Ciolkovskem

Ministrstvo za šolstvo Republike Bilorus EE "Vitebska državna tehnološka univerza" Tema. Oddelek za teoretično in uporabno matematiko "Rows". razbil izr. Є.B. Duninoyu. Glavni

Zvezna agencija za izobraževanje Zvezna državna agencija za ustanovitev strokovnega izobraževanja ZVEZNA UNIVERZA PIVDENNY R. M. Gavrilova, G. S. Kostetska Metodika

Tema Riadi Fur'є Praktična uporaba Riadi Fur'є za ortogonalnimi sistemi funkcij

TEORIJA DOMETA Teorija serij je najpomembnejša matematična analiza skladišča in poznavanje tako teoretičnih kot numeričnih praktičnih poročil. Razr_znyayut številne številke in funkcije.

ЗМІСТ VRSTA FUR'Є 4 Razumevanje periodične funkcije 4 Trigonometrično polje 6 3 Ortogonalni sistemi funkcij 4 Trigonometrična serija Fur'є 3 5 Vrstica Fur'є za dečke in neparne funkcije 6 6 Postavitev

Zvezna agencija za izobraževanje Moskovska državna univerza za geodezijo in kartografijo (MІIGAIK)

Predavanje 4. Analiza harmonije. Serija periodičnih funkcij Fur'є. Analiza harmonije

TEMA V VRSTA FUR'Є PREDAVANJE 6 Postavitev periodičnih funkcij v seriji Fur'є Bagato procesov, ki se pojavljajo v naravi in ​​tehnologiji, se lahko ponavljajo s pevskimi pozivi eno uro. Takšni procesi

METODOLOŠKI VKAZIVKI PRED ROZRAKHUNKOVIKH ZAVDAN NA TEČAJU VISCHO MATEMATIKE "ZVICHAYNI DIFERENCY RIVNYANNYA RANGE Podviyni INTEGRALI" DEL SH TEMATSKA VRSTA

6 vrstic Fur'є 6 Ortogonalni sistemi funkcij Vrste Fur'є v ortogonalnih sistemih funkcij Funkcije ϕ () in ψ (), vrednosti in integracija na vrhu [,], se v celoti imenujejo ortogonalne

VARIACIJE INTEGRAL. Integral sumi singularnega integrala Nehai ima funkcijo y = f (), dodeljeno obliki [, b], de< b. Разобьём отрезок [, b ] с помощью точек деления на n элементарных

5 vrstic korakov 5 vrstic korakov: vrednost, območje razlike Funkcionalna vrstica v obliki (a + a) + a () + K + a () + K a) (, (5) de, a, a, K , a, k deyaki številke, pokličite državno serijo Številke

UNIVERZA BILORUSKI DERŽAVNI FAKULTETA ZA UPORABNO MATEMATIKO IN INFORMATIKO

Nanj položi deyaki. zadnjico. Poznamo vsoto neskončnega geometrijskega napredka.Formula izraza vneme je a + aq + ... + aq n + ... (a). a n = aq n. Številni del sumija. Če je q =, potem

Zavdannya 1.1. Če želite izvedeti iz določene regije odločitev iz iste ničle, je odločitev y = y (x) diferencialne enačbe, ki je zadovoljna z dodelitvijo regionalnih umov (upravitelj Sturm-Livilya).

Matematična analiza Tema: Petje Integrali Nevlasny Lektorica Pakhomova Є.G. 2017 str. ROZDIL II. Pevski integral te jogo dodatke 1. Pevski integral te jogo moči 1. Glava,

Predavanje 8 4 Vodja Sturm-Livilya Ko opisujem majhen prečni niz strun, vidim problem diferencialne enakosti v zasebnih starejših drugačnega reda.

Pojasnjeno v besedilu: znak se bere jak "pravično" in pomeni, da je pri rivnjanih desničar iz znaka in zlo iz znaka bezlich odgovor, znak IR pomeni brezlich govorne številke, znak IN

82 4. Rozdil 4. Funkcionalna in državna vrstica 4.2. Zaseden 3 4.2. Zaseden 3 4.2 .. Prenos funkcije v Taylorjev niz VREDNOST 4.2 .. Ne vem, funkcija y = f (x) je neomejeno diferencirana na obrobju

MINOBRNAUKI ROSIN FEDERALNA DERZHAVNA BUDGETNA OSVITALNAYA INSTANOVA VISCHOЇ PROFESSIONO USTANOVITE "SAMARSKY DERZHAVNIY TECHNICAL

Zvezna agencija za železniški promet Uralska državna univerza plemičev z Oddelkom za uporabno matematiko

Predavanje 3 Taylorjeve in Maclaurinove vrstice Stagnacija državnih vrstic Razporeditev funkcij v državnih vrsticah vrstic Taylor in Maclaurin

S. A. Lavrenchenko

Integracija funkcije (za Rimana) isti integral Uporabite rešitev nalog 1. Funkcija f (x) = C je integrirana na, tako kot za kakršno koli spremembo ali nihanje točk ξ i integral

1. letnik tečaja. Izvajati Rimanovo funkcijo, ki je 0, m m R (), ki je m, m 0 in druge nekratke, 0, ki je iracionalna, razrivna v kožni racionalni točki in brez prekinitve v koži draženja. Odločitev.

1 2 Zm_st 1 Vrstice Fur'є 5 1.1 Trigonometrična serija Fur'є ............ 5 1.2 Tilki sin & cos ................. .... 7 1.3 Serija krzna v kompleksni obliki 11 1.4 f (x) = ck? .......................

RIVNYANNYA MATEMATIČNA FIZIKA 1. Diferencialna rivnyannya z zasebnimi otroki.

Predavanje 4. Hvilyovi rivnyannya 1. Vivedennya pivnyannya strune 2. Rivnyannya kasneje kolivan striženje 3. Ušesni čepki, platišča 4. Postavitev težav 1. Zmagovalna rivnyannya strune

1. Elektrostatika 1 1. Elektrostatika Lekcija 6 Razvoj sprememb kartezijskih koordinat 1.1. (Tovarniška nastavitev 1.49) Območje z = napolnjeno iz jakosti σ (x, y) = σ sin (αx) sin (βy), de σ, α, β post_yni.

Tema modula Funkcionalni končnici in nizi Moč enakega pomena in vrste

Enakovredno paraboličnemu tipu. Metoda za spreminjanje iste regije Eno regijo tovarne Funkcije naprave Ni eno za isto vrsto toplotne prevodnosti 7 Predavanja 7.1 Enakovredno za parabolični tip. Podil metoda

Predavanje Številčni niz Znaki vrednosti Številski niz Znaki vrednosti Številski niz Znaki vrednosti Številski niz Znaki vrednosti Številski niz Znaki vrednosti Številski niz

35 7 Trigonometrična serija Fur'є Vrstice Fur'є za periodične funkcije s periodo T.

Fakulteta za metalurgijo Oddelek za živilsko matematiko RANGE Metodična navodila Novokuznetsk 5 Zvezna agencija za izobraževanje

Oddelek za matematiko in informatiko Element vse matematike Začetno-metodični kompleks za dijake srednjega strokovnega izobraževanja, ki se začnejo učiti iz oddaljenih tehnologij.

9. Najprej nevrednosti integral 9 .. Naj bo funkcija f () nastavljena na interval I R. Funkcija F () se imenuje primarna funkcija f () za interval I, saj je F () = f () za kateri koli I, to je primarna

DIFERENCIALNE FUNKCIJE ENA ZIMA Razumevanje preprostega, geometrijskega in fizičnega smisla Zavdannya, ustvariti pred razumevanjem primitivnega Oznaka Stosovo S na premico y f (x) v točki A x; f (

Enakovredno hiperboličnemu tipu. Stolpec neinhibiranih in nedokončanih strun. D'Alembertova metoda Neodišavljena struna. D'Alembertova formula Nelinearni niz 3 Predavanje 3.1. Enakovredno hiperboličnemu tipu.

Зміст Vstup. Osnovno razumevanje .... 4 1. Integralna družina Volterri ... 5 Variante gospodinjstva ... 8 2. Resolucija Integralne družine Volterri. 10 Možnosti za gospodinjstvo ... 11

RAZPON. Vrstice številk. Glavna vrednost Nehaija je dana neomejenemu številu Virazovih števil (neomejena vsota) a, a 2, ..., an, ... ai = a + a 2 + + an + ... () i = to imenujemo številska vrsta. Številke

8. Koračne vrstice 8 .. Funkcionalna vrstica v obliki cn (z) n, (8.) n = de cn je številčno zaporedje, R je fiksno število in z R se imenuje vrstica stanja s parametri c n . Vicone zamenja zmagovalce

~ ~ Nepomembni in nepomembni integrali Razumevanje primordialnega in nepridejenega integrala. Oznaka: Funkcija F se imenuje prva vrstica glede na funkcijo f, kot tudi funkcijo pritrditve

3724 VRSTICE CRATNI І KRIVOLINIINI INTEGRALS 1 ROBOCH PROGRAM ROSDILIV "VRSTICI CRATNI І CRYVOLINIINI INTEGRALS" 11 Številčni niz Razumeti vrsto števil Moč števil

JEJ. RUDIJ MATEMATIČNA ANALIZA. ŠTEVILKE IN FUNKCIONALNE VRSTICE NOVOSIBIRSK 200 2 MINOBRNAUKI ROSIN GOU VPO "NOVOSIBIRSKY DERZHAVNIY PEDAGOGICHNY UNIVERSITY" О.М. Rudiy MATEMATIČNA ANALIZA.

PREDAVANJE N 7. Taylorjeve vrstice in Taylorjeve vrstice ... Taylorjeve vrstice ... Taylorjeve vrstice ...

TRG RIVNIANNYA Zmist TRG RIVNIANNYA ... 4. ta zadnji kvadrat rivnyan ... 4 ..

ROZDIL ZAVDANNIA S PARAMETRI Komentarji Upravljanje s parametri je tradicionalno zložljivi objekti pri strukturah EDI, tako da lahko uporabite vse metode in metode reševanja otrok.

Diferencialni izračun Uvedeno v matematično analizo Intersekcijske funkcije. Rozkritta nevrednosti na mejah. Funkcije so podobne. Pravila diferenciacije. Zasosuvannya obhіdnoї

Serija Fur'є ortogonalnih sistemov funkcij Z vidika algebre enakovrednost defunkcij danega razreda a - zmogljivost iz R, vendar C preprosto pomeni, da je vektor linearna kombinacija vektorjev

1. Pevski integral 1.1. Naj je f obkrožen s funkcijo, nastavljeno na obliko [, b] R. Rozbittyam vidrizka [, b] imenuje ta niz točk τ = (x, x 1, ..., xn 1, xn) [, b] , uh = x< x 1 < < x n 1

Glavne stopnice Vrstice a a a Pogled vrstice a a a a a () se imenujejo statični, de, a, pooperativni, imenovani funkcionarji v vrsti.

Postavitev v vrsto FUR' fantov in neparnih funkcij.

Postavitev vrstice parnih in neparnih funkcij FUR'є Funkcije f (x), dodeljene obliki \ -1, de I> 0, se imenujejo parne, saj je graf parnih funkcij simetričen in os ordinat. Funkcija f (x), dodeljena obliki J), de I> 0, se imenuje neparna, saj je graf neparnih funkcij simetričen glede na storž koordinat. zadnjico. a) Funkcije є seznanjene na alternativah | -jt, jt), to je za vse x e b) Funkcije so neparne, to je, naštevanje v vrsti Fur'є fantov in neparnih funkcij; Fur'є za funkcije z dolgo obdobje Kompleksni zapis za število Fur'є Riadi Fur'є za številne ortogonalne sisteme funkcij Število Fur'є za ortogonalni sistem Minimalna moč funkcije sistema Ohlapnost sistema (x) de nі za fante, nі za neparne funkcije, oskіlki Nekhai funkcija f (x), kot misli iz izrekov 1, є seznanjene na kot x |. Todi vse tobto. / (x) cos nx je seznanjena funkcija in f (x) sinnx je neparna. S tem funkcija parne funkcije / (f) dokonča funkcijo Otzhe, številka parne funkcije ma viglyad 00 Yaksho f (x) je neparna funkcija na izhodu [-tg, ir |, nato funkcija ni seznanjena z , in seštevek f (x) sin nx je parna funkcija. V takem rangu je mogoče videti vrsto neparnih funkcij Fuhr'є Dodatek 1. Presledki v nizu Fur'є na podobni funkciji -x ^ x ^ n 4 Torej kot funkcija para in če smo zadovoljni z izreki 1, potem poznamo kofіtsієnti Fur'є. Mamo Dvіchі integracija v delih, otrimamo, tako da je število Fur'є te funkcije viglyadє naslednje: vseeno je v odprtem pogledu vrednost poštena za kateri koli x €, tako kot v točkah x = ± ir obstaja število f (x) = x2, fragmenti Grafi funkcije f (x) = x in vsota dane vrstice so podani na sl. Spoštovanje. Celotna serija Fur'є vam omogoča, da poznate vsoto ene od številskih vrst, ki se konvergira in je sama pri x = 0 deaktivirana, vendar aplikacija 2. Razširi se v seriji Fur'ê na intervalu funkcija / (x) = x. Funkcija / (x) je zadovoljiva za izrek 1, prav tako pa je mogoče razširiti v vrsto Fur, ki se preko neparne funkcije funkcije integrira skupaj, poznamo funkcijo funkcije funkcije funkcije glede na to, da se vrstica Fur vseh x točk x - ± tg vsota števila Fur'є ne znebi vrednosti funkcije / (x) = x, nekatere najpomembnejše drže so v podobnem [- *, i-] vsota števila ê periodičnih naprednih funkcij / (x) = x; njen graf je prikazan na sl. 6. § 6. Razporeditev funkcije, podane pogonu, v vrsti za sinusi ali po kosinusih. Pomen osrednje funkcije za dostavo 0 | mogoče je biti v drugem rangu. Možno je na primer uporabiti funkcijo / na vozilu] tako, schob /. Imam veliko vipadku za povedati, no) "povišal v vidrizok 0] od mladega čina"; її število Fur'є maščevanje lishe kosinusi. Ker je funkcija / (f) pomembna za obliko [-l-, mc], torej, če je funkcija neparna, če se zdi, da / "je povišana v obliko [- *, 0] z neparnim rangom"; Vso vrsto Fur'є bomo zamenjali samo s sinusi. Prav tako je koža obdana z grudičasto monotono funkcijo / (f), dodeljena je nadomestnemu, možno je razširiti v vrsti Fur'є і vzdolž sinusov, і vzdolž kosinusov Uporaba 1. Funkcije v vrsti vrtnic 'є: a) po kosinusih; b) za sinusi. M Funkcija je dana za seznanjene in neparne promocije v vіdrizoks | -x, 0), če so prepletene, da so shmatkovo-monotone. a) Neprekinjeno / (z) na izhodu 0) a) Neprekinjeno j \ x) na izhodu (-tg, 0 | moški rang (slika 7), to je vrstica Fur'є i matime viglyad P = 1 de učinkovitost Fur 'є, b) Nadaljujte / (z) v obliki [-x, 0] neparno (slika 8). Todi її število Fur'є §7. Serija Fur'є za funkcijo z določeno obdobjem Nehai funkcija fix) je periodika z obdobjem 21,1 ^ 0. Ta funkcija F (t) = / ^ tj bo periodična funkcija argumenta t iz obdobja in jo je mogoče razširiti na vrsto Fur'є. , Za obstanek na oblasti in za periodične funkcije z določenim obdobjem 21. Zokrem, ki je pridobil svojo moč in zadostno, da označi porazdelitev funkcij v vrsti Fur'є. Uporaba 1. Razširitev niza Fur'є je periodična funkcija z obdobjem 21, ki je podana obliki [- /, /] s formulo (slika 9). Torej, ko je podana funkcija para, potem je število Fur'є maє viglyad podano številnim Fur'є, ki poznajo vrednosti funkcij Fur'є, upoštevamo en pomemben pomen moči periodičnih funkcij. Izrek 5. Če je funkcija obdobja T integrirana, potem je to število in se prikaže enakost m. Se pravi, da integracija ne temelji na razliki med obdobjem ceste T, ampak je enak pomen prav iz položaja pogona na številčni osi. Pošteno, Robimo bo zamenjal zlobnost iz drugega Integrala, vvazhayuchi. Tse daє in і, tudi geometrijsko, moč pomeni, da območja, zasenčena na sl. 10 regij, ki so si med seboj enake. Zokrem, za funkcijo f (x) s točko je sprejemljivo, če je vrsta FUR' tipov in neparnih funkcij postavljena v vrsto za sinusi ali po kosinusih. Fur'є funkcija Fur' serija po ortogonalnih sistemih Minimalna moč učinkovitosti Besselove enakosti Parseval zaprtih sistemov Rotacija in zaprtost sistemov Aplikacija 2. Funkcija x ê periodična iz obdobja Zaradi neparne narave te funkcije, brez štetja integralov, jo je mogoče uporabiti, če pa je komu dana moč, vzmet, ki je funkcija periodičnih funkcij f (x) število (pomensko, funkcija je cos - in sin je lahko točka 2 /). Uporaba 3. Odpiranje števila Fur'є je podano na intervalu s funkcijo s periodo 2x (slika 11). 4 Poznamo funkcionalnost funkcije. Otzhe, niz Fur'є bo viden takole: V točki x = jt (točka rezanja prvega rodu) maєmo §8. Celovit zapis za številne Fur'є V celotnem odstavku vikoristovuyutsya deyaki elementi kompleksne analize (div. Razdil XXX, de vse diy, ki se izvaja tukaj s kompleksnimi virazami, suvoro obrobljene). Naj se funkcija f (x) zadovolji z dovolj prostora v vrsti Fur'є. Na primer, v kompleksni obliki (3) je mogoče prikazati smer Vikoristove formule Eilerja. Znano je, da virazi kofіtsієntіv prek integraral. Podobno lahko preostalo formulo za с „, с_п і с zapišemo takole:. ... Funkcije se imenujejo kompleksne funkcije Fur'є funkcije Za periodične funkcije iz obdobja), kompleksna oblika je število Fur'є bo vidno v očeh dekofitsinti Sp, ki se izračuna po formulah vrednosti w, kot tudi med aplikacijami. Prostori v kompleksni seriji Fur'є funkcije obdobja. Funkcija je dana zadostnim umom porazdelitve v vrsti Fur'є. Nekhai Know-how kompleksna funkcionalnost Fur'є osrednja funkcija. Mahmo za neparne za fante n, ali krajše. Predstavlyayuchi pomen), prepoznavno rezidualno Veliko, vendar lahko število zapišemo takole: Vrstica Fur'є za ortogonalnimi sistemi funkcij 9.1. Ortogonalni sistemi funkcij Nesmiselno skozi vse (akcijske) funkcije, ki so smiselne in integrirane v kvadrat [a, 6], tako da tako, za neki preprost integral. Zokrema, vse funkcije f (x), brez prekinitve do oblike [a, 6], da so 6], in pomen Lebesgueovih integralov so vključeni v pomen Rimanovih integralov. Viznachennya. Sistem funkcij, de, se imenuje ortogonalni na obliko [a, b \, kot Umov (1) prenos, zokrem, vendar funkcije niso primerne za isto ničlo. Integriran pogovor s Sensei Lebesgueom. Če se vrednost imenuje norma funkcije v ortogonalnem sistemu za kateri koli stroj, se sistem funkcij imenuje ortonormalen. Če je sistem (y> „(g)) pravokoten, potem je sistem Uporaba 1. Trigonometrični sistem je pravokoten v smeri. Sistem funkcij je ortonormalni sistem funkcij, Dodatek 2. Kosinusni sistem і sinusni sistem je ortonormalen. Uvedene so vrednosti ê ortogonalne na smer (0, f |, vendar ne ortonormalne (pri I F-2). Tako kot jih normira COS. da bi funkcija vzpostavila ortonormalni sistem funkcij na poti Zdi se, da je na primer ortogonalnost Legendrovih polinomov. do reda m - I vključno, se pretvori v nič na koncu obrazca [-1,1). Viznachennya. Sistem funkcij (pn (x)) imenujemo ortogonalni na intervalu (a, b) s funkcijo p (x), kjer: 1) za vse n = 1,2, ... Povsod je označen z i pozitivno na intervalu (a, b) za morebitno vinjeto končnega števila točk, kjer se p (x) lahko obrne na nič. Ko smo naredili diferenciacijo v formuli (3), je znano. Lahko pokažemo, da je obračanje Chebishev-Ermita pravokotno na intervalu. Uporaba 4. Sistem Besselovih funkcij (jL (pix) ^ je pravokoten na intervalu nič Besselove funkcije. ortogonalni sistem funkcij v interval (a, 6) in niz (cj = const) se na celotnem intervalu konvergirata k funkciji f (x): sistem je otrimaєmo, scho tsya operatsіya maє, očitno je formalna narava. Tim ni najmanjši, za nekatere ljudi, na primer, če se niz (4) enakomerno konvergira, so vse funkcije neprekinjene in interval (a, 6) je dolgočasen, operacija pa je zakonita. Za nas je prav formalna razlaga hkrati pomembnejša. Otzhe, naj bo funkcija nastavljena. Številke z * veljajo za formulo (5) in lahko zapišemo Serija, ki stoji na desnem delu, se bo imenovala naslednja Fur'є funkcija f (x) in sistem (^ n (i)) - Števila Cn imenujemo funkcije Fur'є funkcija f (x ) za celoten sistem. Znak ~ v formuli (6) pomeni, da so števila Cn povezana s funkcijo / (g) s formulo (5) (za katero se ne prenese, vendar se vrstica na desni strani konvergira, vendar bolj konvergira k funkcija f (x)). Za to je naravno jesti hrano: kakšna moč je tam? Katera vrednost "predstavlja" funkcijo f (x)? 9.3. Vrednost povprečne vrednosti. Zadnji, konvergirajo k elementu] na sredini, kot norma v prostranosti Izrek 6. Zadnji) konvergirajo enako oddaljeno, ne konvergirajo v sredini. M Naj zadnji () ne gre naravnost v smer [a, b] do funkcije / (x). Tse pomeni, da so zvoki naše moči živahni, da bi koža sploh dosegla veliko mamo Otzhe. Zvorotna trdnost je napačna: zadnji () se lahko na sredini zbliža z / (x), vendar ne povsem podobno. zadnjico. Zadnjo stvar je enostavno videti. Enostavno varnostno kopirati, vendar Ale tsya ne deluje zadaj: na primer je, na primer, ne bom super, ampak večinoma, Začenjam vrsto štirih tipov in funkcij brez primere kosinus Vrstica Fur'є za funkcije s obdobjem pred obdobjem Kompleksni zapis za serijo Fur'є Riadi Fur'є za zunanje ortogonalne sisteme funkcij Vrstica Fur'є zadaj ortogonalni sistem Minimalna moč funkcij Fury-šivi sistemi Ohlapni sistemi Ortonormaliziran sistem Linearna kombinacija de n ^ 1 - je fiksirala celo število, poznamo vrednost zadnjih, za katere je integral najmanjša vrednost. Pisno poročilo je po členu zanimivo, zaradi ortonormalnosti sistema je mogoče prepoznati, da prvi dve dopolnitvi na desnem delu ravnotežja (7) ne ležita, tretjega pa ni mogoče našel. Temu integral (*) doda najmanjšo vrednost pri ak = ck, integral se imenuje srednji kvadratni približek funkcije / (x) linearna kombinacija Tn (x). V takem rangu je povprečni kvadratni približek funkcije / sprejem najnižja vrednost, če. če je Tn (x) 71-a del vsote števila funkcij / (x) za sistemom (. Vazhayuchi ak = ck, s (7) lahko sprejmemo Ekvivalentnost (9) se imenuje isti Bessel. , potem sem zaradi Besselove inertnosti Oskilka precej tukaj, potem je Besselova inertnost možna v močnejši obliki, torej za katero koli funkcijo / več kvadratov funkcij. Torej, ker je sistem ortonormaliziran na podlagi [-x, tg], je nedoslednost (10) pri transpoziciji v osnovni zapis trigonometrične serije Fur'є da Če je f2 (x) integriran, potem bodo s potrebnim umom prepoznane številne indiskrecije v levem delu živcev (11). Parsevalova pariteta Za nekatere sisteme (^ „(x)) lahko znak nedostojnosti v formuli (10) nadomestimo (za vse funkcije / (x) 6 let) kot znak parnosti. Otrimanova pariteta se imenuje parseval-Steklov paritet (um). Besselova identiteta (9) nam omogoča, da sam zapišemo umov (12) v enakovredni obliki Tim, ime uma pomeni, da so deli sumi Sn (x) nizki, da funkcija / (x) konvergira k funkcija / (x) v sredini, tobto. nad normo 6]. Viznachennya. Sistem je ortonormaliziran (imenovan bolj v b2 [ay b], kot da bi bila funkcija čim bolj natančna v kombinaciji v sredini vrstice, bi jo lahko dostavili z velikim številom oddaj, tako da bi lahko bila funkcija za , B \ i za vsako e> 0 obstaja naravno število nq і števila a \, a2y ... za celoten sistem pojdite na f (x) na sredini, tako da za normo lahko pokažete, da je trigonometrična sistem je redek, zvezde so živo čvrste. Izrek 8. Če ji funkcija trigonometrične serije Fur konvergira v povprečju. 9.5. Zaprti sistemi. Potencial in zaprtost sistemov vrednosti. Sistem funkcij \ je ortonormalen, imenujemo ga zaprt, kot da v prostoru Li \ a, b) ni funkcija, ki je ortogonalna na vse funkcije. Desno 1. Postavite vrstico Fur'є v funkcijo intervala (-ya-, z) 2. Postavite vrstico Fur'є v funkcijo intervala (-tg, tg) 3. Postavite vrstico Fur'є v intervalna (-tg, tg) funkcija 4. Postavite serijo Fur'є v interval (-jt, tg) funkciji 5. Postavite serijo Fur'n v interval (-tg, tg) s funkcijo f (x) = x + x. 6. Postavite do vrstice Fur'є v funkciji intervala (-jt, tg) n 7. Postavite do vrstice Fur'є v funkciji intervala (-tg, z) / (x) = sin2 x. 8. Postavite do vrstice Fur'є v funkciji intervala (-tg, jt) f (x) = y 9. Postavite do vrstice Fur'є v funkciji intervala (-tt, -k) / (x ) = | greh x |. 10. Postavite niz Fur'є v interval (-ya-, mr) funkcijo / (x) = §. 11. Funkcijo f (x) = sin § postavimo do vrstice Fur'є v interval (-tg, tg). 12. Razširiti vrstico Fur'є s funkcijo f (x) = n -2x, podano v intervalu (0, x), in jo potisniti v interval (-x, 0): a) kot fant; b) neparni rang. 13. Vrstico Fur postavimo za sinuse funkcije f (x) = x2, podane v intervalu (0, x). 14. Razčlenite niz Fur'є funkcij / (x) = 3, podanih v intervalu (-2,2). 15. Funkcijo f (x) = | x | razširimo na vrstico Fur'є, podano v intervalu (-1,1). 16. Postavite Fur vrstico za sinuse s funkcijo f (x) = 2x, podano v intervalu (0,1).