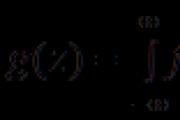Rivnyannya med mrtvimi. Opis rešitve

30.07.2020

V teh temah si lahko ogledamo način ponovnega pregleda funkcije za njen zgornji diferencial, vendar vrstni red uporabimo s končno analizo rešitve.

Buvaє tako, da se lahko diferencialna enačba (DC) oblike P (x, y) d x + Q (x, y) d y = 0 maščuje v levih delih istih diferencialov obstoječih funkcij. Potem lahko poznamo celotni integral DK, saj lahko vnaprej vidimo funkcijo celotnega diferenciala.

zadnjica 1

Poglejmo poravnavo P (x, y) d x + Q (x, y) d y = 0 . Zapis levega dela ima diferencial trenutne funkcije U(x, y) = 0. Za katere je mogoče vykonuvatitsya Umov ∂ P ∂ y ≡ ∂ Q ∂ x .

Zadnji diferencial funkcije U (x, y) = 0 lahko izgleda d U = ∂ U ∂ x d x + ∂ U ∂ y d y . Prosimo, razumejte, da je ∂ P ∂ y ≡ ∂ Q ∂ x sprejemljivo:

P (x, y) d x + Q (x, y) d y = ∂ U ∂ x d x + ∂ U ∂ y d y

∂ U ∂ x = P (x, y) ∂ U ∂ y = Q (x, y)

Ko smo prvo enako spremenili iz odstranjenega sistema enakih, lahko upoštevamo:

U (x, y) = ∫ P (x, y) d x + φ (y)

Funkcijo φ (y) lahko poznamo iz drugega enakega sistema:
∂ U (x, y) ∂ y = ∂ ∫ P (x, y) dx ∂ y + φ y "(y) = Q (x, y) ⇒ φ (y) = ∫ Q (x, y) - ∂ ∫ P (x , y) dx ∂ ydy

Tako smo vedeli, da bomo potrebovali funkcijo U (x, y) = 0.

zadnjica 2

Najdi za DC (x 2 - y 2) d x - 2 x y d y = 0 je velika rešitev.

Rešitev

P (x, y) = x 2 - y 2, Q (x, y) = - 2 x y

Premislimo, kako um ∂ P ∂ y ≡ ∂ Q ∂ x:

∂ P ∂ y = ∂ (x 2 - y 2) ∂ y = - 2 y ∂ Q ∂ x = ∂ (- 2 x y) ∂ x = - 2 y

Naši umi so hudobni.

Na podlagi izračuna lahko ugotovimo visnovok, da je levi del zunanje razdalje keruvane zgornji diferencial delujoče funkcije U (x, y) = 0 . To funkcijo bi morali poznati.

Lestvica (x 2 - y 2) d x - 2 x y d y

∂ U ∂ x = x 2 - y 2 ∂ U ∂ y = - 2 x y

Integrirati preko x pred poravnavo sistema:

U (x, y) \u003d ∫ (x 2 - y 2) d x + φ (y) \u003d x 3 3 - x y 2 + φ (y)

Zdaj razlikovanje glede na y in odštevanje rezultata:

∂ U ∂ y = ∂ x 3 3 - x y 2 + φ (y) ∂ y = - 2 x y + φ y "(y)

Ko smo sistem spremenili na drugo raven, lahko predpostavimo: ∂ U ∂ y = - 2 x y . Tse pomeni kaj
- 2 x y + φ y "(y) = - 2 x y φ y" (y) = 0 ⇒ φ (y) = ∫ 0 d x = C

de S - Postal sem precej.

Zahtevano: U (x, y) \u003d x 3 3 - x y 2 + φ (y) \u003d x 3 3 - x y 2 + C. Zgornji integral zunanje poravnave je ê x 3 3 - x y 2 + C = 0.

Oglejmo si še eno metodo znakhodzhennya funktsії za vіdomim povnym diferencial. Prenos krivolinijskega integrala iz fiksne točke (x 0 , y 0) v točko s spreminjajočimi se koordinatami (x , y):

U (x, y) = ∫ (x 0, y 0) (x, y) P (x, y) d x + Q (x, y) d y + C

Pri različnih vrednostih integrala je nemogoče ležati na poti integracije. Lahko ga vzamemo kot način za integracijo lamana, črte so razvrščene vzporedno s koordinatnimi osmi.

zadnjica 3

Poiščite globalno rešitev diferencialne enačbe (y - y 2) d x + (x - 2 x y) d y = 0 .

Rešitev

Ponovno preverimo, ali je Umova formula ∂ P ∂ y ≡ ∂ Q ∂ x:

∂ P ∂ y = ∂ (y - y 2) ∂ y = 1 - 2 y ∂ Q ∂ x = ∂ (x - 2 x y) ∂ x = 1 - 2 y

Zdi se, da je levi del diferencialne enačbe predstavljen z najvišjo diferencialom trenutne funkcije U(x, y) = 0 . Da bi poznali to funkcijo, je treba izračunati krivolinijski integral točk (1 ; 1) prej (x, y). Vzemimo to kot način za integracijo lamana, pojdimo naravnost y=1 od točke (1, 1) do (x, 1) in nato od točke (x, 1) do (x, y):

∫ (1 , 1) (x , y) y - y 2 dx + (x - 2 xy) dy = = ∫ (1 , 1) (x , 1) (y - y 2) dx + (x - 2 xy ) dy + + ∫ (x, 1) (x, y) (y - y 2) dx + (x - 2 xy) dy = = ∫ 1 x (1 - 1 2) dx + ∫ 1 y (x - 2) xy) dy = (xy - xy 2) y 1 \u003d = xy - xy 2 - (x 1 - x 1 2) = xy - xy 2

Odvzeli smo celotno rešitev diferencialne enačbe v obliki x y - x y 2 + C = 0.

zadnjica 4

Izberite globalno rešitev diferencialne enačbe y cos x d x + sin 2 x d y = 0.

Rešitev

Reverzibilno je, da je chi potrošni ∂ P ∂ y ≡ ∂ Q ∂ x .

Oskіlki ∂ (y · cos x) ∂ y = cos x , ∂ (sin 2 x) ∂ x = 2 sin x · cos x , potem um ne bo zmagal. Tse pomeni, da levi del diferencialne enačbe ni ista diferencialna funkcija. Tse diferencialna poravnava s spremembami, ki so razdeljene, in za to različico so primerni drugi načini reševanja.

Kako ste se spomnili pomilostitve v besedilu, bodite prijazni, poglejte in pritisnite Ctrl + Enter

Postavitev problema v perspektivi dveh svetov

Ponovno odkrivanje funkcij števila sprememb za njenim novim diferencialom

9.1. Postavitev problema v dvosvetovnem pogledu. 72

9.2. Opis rešitve. 72

To je eden od dodatkov krivolinijskemu integralu druge vrste.

Glede na popolno razliko funkcije dveh sprememb:

Spoznajte funkcijo.

1. Torej, saj ni mogoče vsak um videti kot nov diferencial pevske funkcije U(x,y), potem je treba obrniti pravilnost izjave naloge, da bi jo obrnil, je treba premisliti, da ima um dovolj novega diferenciala, kot bi lahko izgledala funkcija 2-x spremembe. Tsya umova vyplivaet z enakovrednostnimi trditvami (2) in (3) v izreku prejšnjega odstavka. Takoj ko je bila imenovana umova vikonan, je bila naloga sprejeti odločitev, tako da je funkcija U(x,y) se lahko podaljša; če um ni ubit, potem ni rešitve, zato funkcije ni mogoče obnoviti.

2. Funkcijo za njenim zgornjim diferencialom je mogoče poznati na primer za dodatni krivolinijski integral II vrste, potem ko smo izračunali yogo v premici, ki je fiksna točka ( x 0 ,y 0) ta sprememba točke ( x; y) (Mal. osemnajst):

V tem rangu je bilo odvzeto, da je krivolinijski integral 2. vrste kot popoln diferencial dU(x,y) dobra vrednost funkcije U(x,y) na koncu in koruznih točkah integracijske črte.

Zdaj, ko poznamo rezultat, je treba zagotoviti nadomestek dU v krivolinijsko integralno virazo in izvedite izračun integrala za lamanom ( ACB), vrakhovuyuchi yogo neodvisnost v obliki integracijskih linij:

na ( AC): na ( JZ) :

(1)

V tem rangu je bila odpravljena formula, za pomoč katere se uporablja funkcija 2. zamenjave za njen zgornji diferencial.

3. Možno je izboljšati funkcijo za njen zgornji diferencial d(U+ const) = dU. Zato se kot rezultat izpolnitve naloge upoštevajo neosebne funkcije, da se na trajnem dodatku izdeluje ena vrsta.

Uporabi (inovacija funkcije dveh zamenjav za tretji diferencial)

1. Vedeti U(x,y), kot dU = (x 2 – y 2)dx – 2xydy.

Ponovno preverimo celoten diferencial uma glede funkcije dveh sprememb:

V mislih novega diferenciala, vikonano, tudi funkcija U(x,y) je mogoče obnoviti.

Perevіrka: - Tako je.

predlog: U(x,y) = x 3 /3 – xy 2 + C.

2. Poznati funkcijo kot npr

Pregledamo potrebno in zadostno poznavanje skupnega diferenciala funkcij treh sprememb: , , kot ga poda viraz.

Pri rozvyazuvanіy nalog

vse misli novega diferenciala viconana, zato se lahko funkcija obnovi (naloga je pravilno zastavljena).

Funkcijo dodamo s pomočjo krivolinijskega integrala druge vrste, ki jo izračunamo vzdolž črte, ki je fiksna točka in točka spremembe, tako

(Tsya rivnіst vyvoditsya tako sama, kot v dvosvetovnem razpoloženju).

Po drugi strani krivolinijski integral II vrste v primeru popolnega diferenciala ne more ležati v obliki linearne integracije, lažje ga je postaviti za laman, ki je sestavljen iz navitij, vzporednih s koordinato osi. Če je točka fiksna, za preprostost vzemite točko z določenimi številčnimi koordinatami, poleg tega tako, da imajo točke in na celotni liniji integracije mentalno osnovo krivolinijskega integrala (tako da so funkcije, i, neprekinjene). Če želite izboljšati to spoštovanje te naloge, lahko vzamete fiksno točko, na primer točko M 0. Todi na koži iz nog lamanoi matimemo

10.2. Izračun površinskega integrala prve vrste. 79

10.3. Deyaki programi površinskega integrala prve vrste. 81

Kakšen je standardni videz $P \ levo (x, y \ desno) \ cdot dx + Q \ levo (x, y \ desno) \ cdot dy = 0 $, v tem primeru je levi del zadnji diferencial dejanska funkcija $ F \ left ( x,y\right)$, se imenuje enaka novi diferenciali.

Enačbo v najnovejših diferencialih lahko prepišemo kot $dF \ levo (x, y \ desno) = 0 $, de $ F \ levo (x, y \ desno) $ - taka funkcija, da $ dF \ levo (x, y \desno)=P\levo(x,y\desno)\cdot dx+Q\levo(x,y\desno)\cdot dy$.

$dF\left(x, y\desno) = 0$: $\int dF\left(x, y\desno) = F\left(x, y\desno)$; integral v ničlem desnem delu dražje dokaj konstantne $C$. Tako je lahko končna rešitev te enačbe v implicitni obliki videti kot $ F \ levo (x, y \ desno) = C $.

Da bi bila ta diferencialna enakost enaka v drugih diferencialah, je potrebno in zadostno, da je Umov $\frac(\partial P)(\partial y) =\frac(\partial Q)(\partial x) $. Če je dodeljen pametni vikonan, potem obstaja taka funkcija $F\left(x,y\right)$, za katero lahko napišete: $dF=\frac(\partial F)(\partial x) \cdot dx+ \frac(\delni F)(\delni y) \cdot dy=P\left(x,y\desno)\cdot dx+Q\left(x,y\desno)\cdot dy$ delno F)(\delno x) = P\left(x,y\desno)$ i $\frac(\delni F)(\delni y) = Q\left(x,y\desno)$.

Integriran pred $\frac(\delni F)(\delni x) =P\left(x,y\right)$ nad $x$ in $F\left(x,y\right)=\int P\ left( x,y\right)\cdot dx +U\left(y\right)$, kjer je $U\left(y\right)$ zadostna funkcija od $y$.

Vzemimo to tako, da je izpolnjen še en spin $\frac(\delni F)(\delni y) = Q\left(x, y\right)$. Za katerega lahko razlikujemo $F\left(x,y\right)$ glede na $y$ in izenačimo rezultat z $Q\left(x,y\right)$. Izbirno: $\frac(\delni )(\delni y) \left(\int P\left(x,y\right)\cdot dx \right)+U"\left(y\right)=Q\left( x,y\desno)$.

Nadaljnja rešitev je:

za preostalo enakost poznamo $U"\left(y\right)$;
integrabilni $U"\left(y\right)$ in znani $U\left(y\right)$;
zamenjava $U\left(y\right)$ za enakost $F\left(x,y\right)=\int P\left(x,y\right)\cdot dx +U\left(y\right)$ in funkcija $F\left(x,y\right)$ je rezidualno vzeta.

Poznamo razliko:

$U"\left(y\right)$ je integrabilen glede na $y$ in $U\left(y\right)=\int \left(-2\right)\cdot dy =-2\cdot y$ je znan.

Znani rezultat: $F\left(x, y\desno) = V\left(x, y\desno) + U\left(y\right) = 5\cdot x\cdot y^(2) +3\cdot x\cdot y-2\cdot y$.

Rešitev lahko zapišemo na naslednji način: $F \ levo (x, y \ desno) = C $ in sama:

Znana zasebna rešitev $F\left(x,y\right)=F\left(x_(0) ,y_(0) \right)$, kjer je $y_(0) =3$, $x_(0) =2 $:

Zasebna rešitev je lahko videti tako: $5 cdot x cdot y ^ (2) +3 cdot x cdot y-2 cdot y = 102 $.

Imenovanje 8.4. Diferencial enak umu

de
imenujemo enaka drugim diferencialom.

S spoštovanjem, da je del lva tega enak zgornjemu diferencialu obstoječe funkcije.
.

Na nezaslišanem posestvu lahko plačate davke (8,4) na ogled

Namestnik enak (8.5) je lahko enak

izpeljavo takšne integralne izravnave (8.4). Tako je za rešitev enačbe (8.4) potrebno poznati funkcijo
. Vіdpovіdno do vzdannya vnyannia (8.4), morda

(8.6)

funkcijo
vedeli bomo, kot funkcija, kot zadovoljitev enega od teh umov (8.6):

de - precej funkcija, kot odlaganje vode .

Funkcija
biti prikazan tako, da je bil izraz drugega uma zmagovit (8.6)

(8.7)

Z virazu (8.7) in funkcija je določena
. Njeno pošiljanje v viraz za
da otrimuyut zagalny іntegrа vikhіdnogo іvnyannya.

Naloga 8.3. Integrirajte reko

tukaj
.

Otzhe, tse rіvnyannya je v najnovejših diferencialih priveden na vrsto diferenciala rіvnyan. funkcijo
pošalimo se

Z druge strani,

Na številne vipadkiv umov
ne moreš zajebati.

Ravno tako je enak tipu, ki ga gledamo, pomnožiti s tako imenovanim integrirnim multiplikatorjem, ki je v divjem razpoloženju le funkcija oz .

Kako ima ena enaka integrirni množitelj, ki ga je mogoče le vložiti , potem se formuli dodeli vin

de uprizoritev je lahko manj funkcionalna .

Podobno, kako integrirati množitelj, kako vložiti le nekaj , Odvisno od formule

de uprizoritev
je lahko manj funkcionalna .

Vidsutnіst pri spodbujanju spіvvіdnіshnyah, na prvem koraku spremembe , in drugi - zminnoyu ê predznak osnove integrirnega množitelja za dano izravnavo.

Naloga 8.4. Naj bo cena enaka v zadnjih razlikah.

Poglejmo nastavitev:

Tema 8.2. Linearna diferencialna poravnava

Imenovanje 8.5. Diferencialna poravnava
se imenuje linearna, kot da bi bila linearna funkcija , ji všeč in se ne maščujejo za ustvarjanje funkcije shukano in її pokhіdnoї.

Pogled od zgoraj na linearno diferencialno poravnavo je podoben naslednjemu:

(8.8)

Kako spivvіdnoshnі (8.8) del pravic
, Vzemi enako se imenuje linearna homogena. Imejte vipadku, če je desni del
, Takšna izenačitev se imenuje linearna heterogena.

Pokažimo, da je enačbo (8.8) mogoče integrirati s kvadraturami.

Na prvi stopnji si lahko ogledamo linearno enotnost.

Takšna je enaka enakim spremembam, ki se delijo. Prav,

;

Preostanek spіvvіdnoshnja vznachaє zagalne rіshennya linearno enotno rіvnyannia.

Za iskanje divje rešitve linearne, heterogene poravnave se uporablja metoda variacije podobne postiynoy. Ideja metode je, da je rešitev linearne neenakomerne poravnave videti kot rešitev enotne enakomerne poravnave, proteo je precej hiter zamenjati z drugo funkcijo
, kaj je namen imenovanja. Oče, prosim:

(8.9)

Zamenjava za spіvvіdnoshennia (8.8) virazi, vіdpovіdnі
і
, prevzeto

Če nadomestijo preostalo virazo v spivvіdnenni (8.9), pridobijo globalni integral linearne nehomogene poravnave.

V tem vrstnem redu je glavna rešitev linearne neenakomerne poravnave označena z dvema kvadraturama: globalna rešitev linearne enotne poravnave in končna rešitev linearne neenakomerne poravnave.

Naloga 8.5. Integrirajte reko