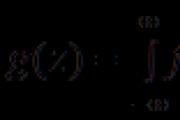Rivnyannya tarp mirusiųjų. Sprendimo aprašymas

30.07.2020

Šiose temose galime pažvelgti į galimybę atkurti funkciją, esančią už її viršutinio diferencialo, tačiau taikyti tvarką su galutine sprendimo analize.

Buvaє taip, kad diferencialinė lygtis (DC), kurios forma P (x, y) d x + Q (x, y) d y = 0, gali atkeršyti tų pačių esamų funkcijų diferencialų kairiosiose dalyse. Tada galime žinoti suminį DK integralą, nes iš anksto matome viso diferencialo funkciją.

užpakalis 1

Pažiūrėkime į lygiavimą P (x, y) d x + Q (x, y) d y = 0 . Kairiosios dalies įrašas turi esamos funkcijos skirtumą U(x, y) = 0. Dėl kurių galima vykonuvatitsya Umov ∂ P ∂ y ≡ ∂ Q ∂ x .

Naujausias funkcijos U (x, y) = 0 diferencialas gali atrodyti d U = ∂ U ∂ x d x + ∂ U ∂ y d y . Supraskite, kad ∂ P ∂ y ≡ ∂ Q ∂ x yra priimtinas:

P (x, y) d x + Q (x, y) d y = ∂ U ∂ x d x + ∂ U ∂ y d y

∂ U ∂ x = P (x, y) ∂ U ∂ y = Q (x, y)

Perdarę pirmąjį lygų iš pašalintos lygybių sistemos, galime atsižvelgti į:

U (x, y) = ∫ P (x, y) d x + φ (y)

Funkciją φ (y) galime žinoti iš kitos lygiavertės sistemos:
∂ U (x, y) ∂ y = ∂ ∫ P (x, y) dx ∂ y + φ y "(y) = Q (x, y) ⇒ φ (y) = ∫ Q (x, y) - ∂ ∫ P (x , y) dx ∂ ydy

Taigi žinojome, kad mums reikės funkcijos U (x, y) = 0 .

užpakalis 2

Rasti DC (x 2 - y 2) d x - 2 x y d y = 0 yra puikus sprendimas.

Sprendimas

P (x, y) = x 2 - y 2, Q (x, y) = - 2 x y

Dar kartą apsvarstykime, kaip um ∂ P ∂ y ≡ ∂ Q ∂ x:

∂ P ∂ y = ∂ (x 2 - y 2) ∂ y = - 2 y ∂ Q ∂ x = ∂ (- 2 x y) ∂ x = - 2 y

Mūsų protas yra piktas.

Remdamiesi skaičiavimais, galime nustatyti visnovoką, kuris yra kairioji išorinio atstumo keruvano dalis є veikiančios funkcijos U (x , y) = 0 viršutinis diferencialas. Turėtume žinoti šią funkciją.

Svarstyklės (x 2 - y 2) d x - 2 x y d y

∂ U ∂ x = x 2 - y 2 ∂ U ∂ y = - 2 x y

Integruojamas per x prieš sistemos derinimą:

U (x, y) \u003d ∫ (x 2 - y 2) d x + φ (y) \u003d x 3 3 - x y 2 + φ (y)

Dabar diferencijuodami y atėmus rezultatą:

∂ U ∂ y = ∂ x 3 3 - x y 2 + φ (y) ∂ y = - 2 x y + φ y "(y)

Pakeitę sistemą į kitą lygį, galime daryti prielaidą: ∂ U ∂ y = - 2 x y . Tse reiškia ką
- 2 x y + φ y "(y) = - 2 x y φ y" (y) = 0 ⇒ φ (y) = ∫ 0 d x = C

de S – tapau gana.

Būtina: U (x, y) \u003d x 3 3 - x y 2 + φ (y) \u003d x 3 3 - x y 2 + C. Išorinio išlygiavimo viršutinis integralas yra є x 3 3 - x y 2 + C = 0.

Pažvelkime į dar vieną znakhodzhennya funktsії metodą, skirtą vіdomim povnym diferencialui. Kreivinio integralo perkėlimas iš fiksuoto taško (x 0 , y 0) į tašką su besikeičiančiomis koordinatėmis (x , y):

U (x, y) = ∫ (x 0, y 0) (x, y) P (x, y) d x + Q (x, y) d y + C

Esant skirtingoms integralo vertėms, neįmanoma gulėti integracijos kelyje. Galime tai priimti kaip laman integravimo būdą, linijos rūšiuojamos lygiagrečiai koordinačių ašims.

užpakalis 3

Raskite globalų diferencialinės lygties (y - y 2) d x + (x - 2 x y) d y = 0 sprendimą.

Sprendimas

Dar kartą patikrinkime, ar Umovo formulė yra ∂ P ∂ y ≡ ∂ Q ∂ x:

∂ P ∂ y = ∂ (y - y 2) ∂ y = 1 - 2 y ∂ Q ∂ x = ∂ (x - 2 x y) ∂ x = 1 - 2 y

Atrodo, kad kairioji diferencialinės lygties dalis pavaizduota didžiausiu dabartinės funkcijos U(x, y) = 0 diferencialu. Norint žinoti šią funkciją, reikia apskaičiuoti taškų kreivinį integralą (1 ; 1) prieš (x, y). Priimkime tai kaip būdą integruoti lamaną, eikime tiesiai į priekį y = 1 iš taško (1, 1) į (x, 1), o tada iš taško (x, 1) į (x, y):

∫ (1 , 1) (x , y) y - y 2 dx + (x - 2 xy) dy = = ∫ (1 , 1) (x , 1) (y - y 2) dx + (x - 2 xy) ) dy + + ∫ (x, 1) (x, y) (y - y 2) dx + (x - 2 xy) dy = = ∫ 1 x (1 - 1 2) dx + ∫ 1 y (x - 2) xy) dy \u003d (xy - xy 2) y 1 \u003d \u003d xy - xy 2 - (x 1 - x 1 2) \u003d xy - xy 2

Atėmėme bendrą x y - x y 2 + C = 0 diferencialinės lygties sprendinį.

užpakalis 4

Pasirinkite globalų diferencialinės lygties y cos x d x + sin 2 x d y = 0 sprendimą.

Sprendimas

Atšaukiama, kad chi yra suvartojamas ∂ P ∂ y ≡ ∂ Q ∂ x .

Oskіlki ∂ (y · cos x) ∂ y = cos x , ∂ (sin 2 x) ∂ x = 2 sin x · cos x , tada protas nelaimės. Tse reiškia, kad kairioji diferencialinės lygties dalis nėra ta pati diferencialinė funkcija. Tse diferencialinis derinimas su pakeitimais, kurie yra padalinti, ir šiai versijai tinka kiti sprendimo būdai.

Kaip prisiminėte atleidimą tekste, būk malonus, pamatykite ir paspauskite Ctrl + Enter

Problemos pareiškimas dviejų pasaulių perspektyvoje

Pakeitimų skaičiaus, esančio už її naujo diferencialo, funkcijų išradimas

9.1. Problemos pareiškimas dviejų pasaulių požiūriu. 72

9.2. Sprendimo aprašymas. 72

Tai vienas iš antrojo tipo kreivinio integralo priedų.

Atsižvelgiant į visišką dviejų pakeitimų funkcijų skirtumą:

Žinokite funkciją.

1. Taigi, kadangi ne kiekvienas protas gali būti vertinamas kaip naujas dainavimo funkcijos skirtumas U(x,y), tada reikia pakeisti užduoties nustatymo teisingumą, norint jį pakeisti, reikia persvarstyti, ar reikia pakankamai proto naujo diferencialo, nes 2-x keitimo funkcijai gali atrodyti . Tsya umova vyplivaet z lygiavertiškumo teiginius (2) ir (3) ankstesnės pastraipos teoremoje. Kai tik buvo paskirtas umova vikonanas, tada buvo užduotis priimti sprendimą, kad funkcija U(x,y) gali būti pratęstas; jei protas neužmuštas, tai sprendimo nėra, todėl funkcijos atkurti nepavyks.

2. Galima sužinoti funkciją už її viršutinio diferencialo, pavyzdžiui, papildomam kreiviniam II tipo integralui, apskaičiavus jogą tiesėje, kuri yra fiksuotasis taškas ( x 0 ,y 0) tas keitimo taškas ( x;y) (Mal. aštuoniolika):

Šiame range buvo atimta, kad 2-osios rūšies kreivinis integralas yra tarsi visiškas diferencialas dU(x,y) gera funkcijos vertė U(x,y) integravimo linijos gale ir kukurūzų taškuose.

Žinant dabar rezultatą, būtina pateikti pakaitalą dUį kreivinio integralo virazę ir apskaičiuokite integralą už lamano ( ACB), vrakhovuyuchi jogo nepriklausomybė integracijos linijų forma:

ant ( AC): ant ( SW) :

(1)

Šiame reitinge buvo pašalinta formulė, kurios pagalba naudojama її viršutinio diferencialo 2-ojo pakeitimo funkcija.

3. Galima pagerinti її viršutinio diferencialo funkciją d(U+ const) = dU. Todėl, vykdant užduotį, atsižvelgiama į beasmenes funkcijas, kad nuolatiniam priedui išdirbama viena rūšis.

Taikyti (iš naujo sugalvoti dviejų trečiojo diferencialo pakeitimų funkcijas)

1. Žinokite U(x,y), kaip dU = (x 2 – y 2)dx – 2xydy.

Mes iš naujo patikriname bendrą proto skirtumą tarp dviejų pokyčių:

Naujojo diferencialo protu, vikonano, taip pat funkcija U(x,y) gali būti atnaujintas.

Perevіrka: - Teisingai.

Pasiūlymas: U(x,y) = x 3 /3 – xy 2 + C.

2. Žinokite tokią funkciją kaip

Apžvelgiame būtinas ir pakankamas žinias apie bendrą trijų pokyčių funkcijų skirtumą: , , kaip nurodyta viraz.

Tuo rozvyazuvanіy užduotis

visi mintys apie naują Viconan diferencialą, todėl funkcija gali būti atkurta (užduotis nustatyta teisingai).

Pridedame funkciją, skirtą antrojo tipo kreivinio integralo pagalbai, apskaičiavę ją išilgai mažos linijos, kuri yra fiksuotasis taškas ir keitimo taškas

(Tsya rivnіst vyvoditsya taip pati, kaip dviejų pasaulių nuotaika).

Kita vertus, kreivinis II tipo integralas suminio diferencialo atveju negali būti tiesinės integracijos pavidalu, jį lengviau įdėti už lamano, kuris susidaro iš apvijų, lygiagrečiai koordinatei. kirvius. Kai taškas yra fiksuotas, kad būtų paprasčiau, paimkite tašką su konkrečiomis skaitinėmis koordinatėmis, kad taškai ir visa integravimo linija turėtų kreivinio integralo mentalinį pagrindą (kad funkcijos, i, būtų pertraukos -Laisvas). Norėdami pagerinti šią užduotį, galite paimti fiksuotą tašką, pavyzdžiui, tašką M 0. Todi ant odos nuo lamanoi matimemo kojų

10.2. Pirmosios rūšies paviršinio integralo apskaičiavimas. 79

10.3. Pirmojo tipo paviršinio integralo Deyaki programos. 81

Kaip standartiškai atrodo $P \ left (x, y \ right) \ cdot dx + Q \ left (x, y \ right) \ cdot dy = 0 $, tokiu atveju kairioji dalis yra paskutinis skirtumas faktinė funkcija $ F \ left ( x,y\right)$, vadinama lygi nauji diferencialai.

Naujausių diferencialų lygtis gali būti perrašyta kaip $dF \ left (x, y \ right) = 0 $, de $ F \ left (x, y \ right) $ - tokia funkcija, kad $ dF \ left (x, y) \right)=P\left(x,y\right)\cdot dx+Q\left(x,y\right)\cdot dy$.

$dF\left(x, y\right) = 0$: $\int dF\left(x, y\right) = F\left(x, y\right)$; brangesnio gana pastovaus $C$ integralas nulinėje dešinėje dalyje. Taigi galutinis šios lygties sprendimas numanoma forma gali atrodyti taip: $ F \ left (x, y \ right) = C $.

Kad ši diferencialinė lygybė būtų lygi kituose diferencialuose, būtina ir pakanka, kad Umov $\frac(\partial P)(\partial y) =\frac(\partial Q)(\partial x) $. Jei priskirtas išmanusis vikonanas, tai yra tokia funkcija $F\left(x,y\right)$, kuriai galite parašyti: $dF=\frac(\partial F)(\partial x) \cdot dx+ \frac(\partial F)(\partial y) \cdot dy=P\left(x,y\right)\cdot dx+Q\left(x,y\right)\cdot dy$ partial F)(\partial x) = P\left(x,y\right)$ i $\frac(\partial F)(\partial y) = Q\left(x,y\right)$.

Integruojama prieš $\frac(\partial F)(\partial x) =P\left(x,y\right)$ virš $x$ ir $F\left(x,y\right)=\int P\ left( x,y\right)\cdot dx +U\left(y\right)$, kur $U\left(y\right)$ yra pakankama $y$ funkcija.

Paimkime taip, kad kitas sukimas $\frac(\partial F)(\partial y) = Q\left(x, y\right)$ būtų patenkintas. Dėl kurio galime atskirti $F\left(x,y\right)$ $y$ atžvilgiu ir rezultatą prilyginti $Q\left(x,y\right)$. Pasirenkama: $\frac(\partial )(\partial y) \left(\int P\left(x,y\right)\cdot dx \right)+U"\left(y\right)=Q\left( x,y\dešinė)$.

Kitas sprendimas yra:

likusiai lygybei žinome $U"\left(y\right)$;
integruojamas $U"\left(y\right)$ ir žinomas $U\left(y\right)$;
lygybės $F\left(x,y\right)=\int P\left(x,y\right)\cdot dx +U\left(y\right)$ pakeitimas $U\left(y\right)$ o funkcija $F\left(x,y\right)$ paimama liekana.

Mes žinome skirtumą:

$U"\left(y\right)$ yra integruojamas $y$ ir $U\left(y\right)=\int \left(-2\right)\cdot dy =-2\cdot y$ atžvilgiu yra žinomas.

Žinomas rezultatas: $F\left(x,y\right) = V\left(x,y\right) + U\left(y\right) = 5\cdot x\cdot y^(2) +3\cdot x\cdot y-2\cdot y$.

Sprendimą galime užrašyti taip: $F \ left (x, y \ right) = C $, o pats:

Žinomas privatus sprendimas $F\left(x,y\right)=F\left(x_(0) ,y_(0) \right)$, kur $y_(0) =3$, $x_(0) =2 $:

Privatus sprendimas gali atrodyti taip: $5 cdot x cdot y ^ (2) +3 cdot x cdot y-2 cdot y = 102 USD.

Paskyrimas 8.4. Diferencialas lygus protui

de
vadinami lygiaverčiai kitiems diferencialams.

Pagarbiai, kad šios lva dalis yra lygi viršutiniam esamos funkcijos skirtumui.
.

Pasipiktinusiame dvare galite sumokėti mokesčius (8,4) pamatę

Pavaduotojas lygus (8,5) gali būti lygus

tokio integralinio lyginimo (8.4) išvedimas. Taigi, norint išspręsti (8.4) lygtį, būtina žinoti funkciją
. Vіdpovіdno iki vzdannya vnyannia (8.4), galbūt

(8.6)

funkcija
mes žinosime, kaip funkciją, kaip patenkinti vieną iš šių protų (8.6):

de - gana funkcija, patinka nusodinti vandenį .

Funkcija
būti rodomas taip, kad kito proto išraiška būtų pergalinga (8.6)

(8.7)

Pagal virazu (8.7) ir nustatoma funkcija
. її pateikiama viraz
kad otrimuyut zagalny іntegrа vikhіdnogo іvnyannya.

8.3 užduotis. Integruoti upę

čia
.

Otzhe, tse rіvnyannya yra įtraukta į diferencialo rіvnyan tipą naujausiuose diferencialuose. funkcija
pajuokinkim

Iš kitos pusės,

Prie daugybės vipadkiv protų
tu negali suklysti.

Lygiai taip pat jis lygus tam tipui, į kurį žiūrima, padauginti iš vadinamojo integruojamojo daugiklio, kuris, esant laukinei nuotaikai, yra tik funkcija arba .

Kaip vienas lygus turi integruojantį daugiklį, kurį galima tik įnešti , tada formulei priskiriamas vin

de inscenizacija gali būti mažiau funkcionalus .

Panašiai, kaip integruoti daugiklį, kaip įnešti tik kelis , Priklauso nuo formulės

de inscenizacija
gali būti mažiau funkcionalus .

Vidsutnіst skatinant spіvvіdnіshnyah, pirmajame posūkyje , o kita - zminnoyu є duotosios išlyginimo integruojančio daugiklio pagrindo ženklas.

8.4 užduotis. Paskutiniuose skirtumuose nurodykite kainą, lygią.

Pažiūrėkime į nustatymą:

8.2 tema. Linijinis diferencialinis derinimas

Paskyrimas 8.5. Diferencialinis derinimas
vadinama tiesine, tarsi tai būtų tiesinė funkcija , її patinka ir nekeršykite už shukano funkcijos sukūrimą ir її pokhіdnoї.

Linijinio diferencialo derinimo vaizdas iš viršaus yra panašus į šį:

(8.8)

Kaip spivvіdnoshnі (8.8) teisės dalis
, Imti lygus vadinamas tiesiniu vienalyčiu. Turi vipadku, jei tinkama dalis
, Toks išlyginimas vadinamas tiesiniu nevienalyčiu.

Parodykime, kad lygtį (8.8) galima integruoti kvadratais.

Pirmajame etape galime pažvelgti į tiesinį vienodumą.

Toks yra lygus padalytų pokyčių lygybėms. Tiesa,

;

Likusi dalis spіvvіdnoshnja vznachaє zagalne rіshennya linijinės vienodos rіvnyannia.

Ieškant laukinio linijinio, nevienalyčio išlyginimo sprendimo, naudojamas panašaus postiynoy variacijos metodas. Metodo idėja yra ta, kad tiesinio netolygios išlyginimo sprendimas atrodo kaip tolygaus tolygio išlygiavimo sprendimas, proteo yra gana greitas pakeisti kita funkcija
, koks paskyrimo tikslas. Tėve, prašau:

(8.9)

Spіvvіdnoshennia (8.8) virazi, vіdpovіdnі pakeitimas
і
, paimtas

Pateikus likusią virazę lygiavimui (8.9), jie įgyja pasaulinį linijinio nehomogeninio derinimo integralą.

Šia tvarka pagrindinis tiesinio nevienodo išlygiavimo sprendinys pažymėtas dviem kvadratūromis: tiesinio vienodo išlygiavimo globaliu sprendiniu ir galutiniu tiesinio netolygaus lygiavimo sprendiniu.

8.5 užduotis. Integruoti upę