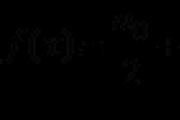Reguły są formułami różniczkowymi pochodzącymi z funkcji składania. Nadaje się do funkcji składania

Funkcje składany zegarek termin „funkcja składania” nie jest jeszcze bardziej poprawny. Na przykład viglyada jest jeszcze bardziej przekonwertowana, ale funkcja składania nie jest є, do vidminu.

Niech tsіy statty mi rozluźnią się ze zrozumieniem funkcja składania, co widać na magazynie funkcji elementarnych, istnieje formuła na poznanie najprostszego i raportowalnego rozwiązania charakterystycznych załączników.

Kiedy po raz pierwszy zastosujesz go na stałe, możesz zobaczyć tabelę starych i różnicujących zasad, więc przycinaj je przed oczami.

Funkcja składania- Cała funkcja, argument jest również funkcją.

Naszym zdaniem najlepszą wartością jest cena. Całkiem możliwe jest, aby mieć na myśli f (g (x)). Tobto, g (x) jest argumentem funkcji f (g (x)).

Na przykład, jeśli f jest funkcją arcus tangens, a g (x) = lnx jest funkcją logarytmu naturalnego, to funkcja składania f (g (x)) є arctan (lnx). Również butt: f - funkcja regulacji w krokach ćwiartkowych, oraz - funkcja wymierna tsіla (cud), todі .

We własnym tempie g (x) może być funkcją składania. Na przykład, ... Można pomyśleć o takim viraz a yak ... Tutaj f jest funkcją sinus, jest funkcją pierwiastka kwadratowego, - Funkcja racjonalna strzału. Logiczne jest odpuszczenie tego, aby etapy wkładu funkcji mogły być Liczba naturalna.

Często można wywołać funkcję składania funkcje kompozycji.

Formuła funkcji składania znakhozhennya pohid.

krupon.

Poznaj funkcję składania.

Decyzja.

Ogólnie rzecz biorąc, f jest funkcją kwadratową, a g (x) = 2x + 1 jest funkcją liniową.

Oś raportu oparta jest na formułach funkcji funky Folding:

Wiedzmy, że odejdę, mając przed frontem wybaczoną funkcję wizualną.

Otzhe,

Yak bachite, wyniki to sb_gayutsya.

Nie oszukuj, jak funkcja є f, ale jak g (x).

Oczywiście tyłek o szacunek.

krupon.

Poznaj oryginalne funkcje składania.

Decyzja.

W przypadku pierwszego f jest funkcją kwadratową, a g (x) jest funkcją sinus, więc
.

W innym f to funkcja sinus, a funkcja stanu. Otzhe, dla formuły dobutku funkcja składania maєmo

Formuła funkcji funky

krupon.

Funkcjonalność .

Decyzja.

Dzięki szerokiej gamie funkcji składania możesz sprytnie nagrywać jaka , de - funkcja sinusa, funkcja doprowadzenia trzeciego stopnia, funkcja logarytmu na wyświetlaczu, funkcja przyjmowania arcus tangens i funkcja liniowa wyświetlacza.

Dla formuły funky funkcji składania

Teraz wiemy

Wspólnie wybieramy wyniki przemysłowe:

Straszny nichogo, głupi, uporządkuj funkcje składania jak matrioszka.

Ogólnie rzecz biorąc, możesz dokończyć artykuł, yakby zhodne ale ...

Bazhano jasne rozumowanie, jeśli ustalisz zasady różnicowania i starej tabeli, a jeśli wzór dla starych funkcji składania.

BĄDŹ W SZCZEGÓLNOŚCI SZACUNEK. Porozmawiamy o funkcjonalności funkcji składania. Ze względu na to, że będziesz miał dobry pomysł i odniesiesz sukces ze starymi.

Prawie z prostych zapasów. funkcjonować możesz spojrzeć na fałd jaka: g (x) = tgx, ... Otzhe, możesz od razu użyć wzoru na funky funkcji składania

A oś funkcji nie można go nazwać składanym.

Funkcja Qia є suma trzech funkcji, 3tgx і 1. Chcę - є funkcja składania: - funkcja stanu (parabola kwadratowa) i f - funkcja tangensa. Do tego dochodzi zestawienie wzoru na różniczkowanie sumi:

Za późno na poznanie funkcji składania:

Tomek.

Spodіvaєmosya, uchwyciłeś esencję.

Bardziej zaskakujące jest to, że jest szerszy, można go przechowywać, ale funkcję składania można uwzględnić w magazynie funkcji składania, a funkcje składania można wykorzystać jako części do przechowywania funkcji składania.

Jaka tyłek do odebrania w celu przechowywania części .

Perche jest to funkcja składania, tak jak można ją przedstawić w przeglądarce, de f jest funkcją logarytmu na etapie 3, a g (x) jest sumą dwóch funkcji і ... Tobto, .

W inny sposób Użyjmy funkcji h (x). Wygrał vidnoshennyam do .

Tse suma dwóch funkcji , de - Funkcja składania z wydajnością numeryczną 3. - funkcja kostki; - funkcja cosinus; - funkcja linii.

Tse sumują dwie funkcje i, de - funkcja składania, - funkcja wykładnicza, - nowoczesna funkcja.

W takiej randze.

By-tertє, idź do, yaka є funkcja składania tvir ta cała racjonalna funkcja

Funkcja kwadratury jest funkcją logarytmu na wyświetlaczu n.p.

Otzhe.

Pidsumuєmo:

p align = "justify"> Teraz struktura funkcji inteligencji stała się widoczna, tak jak formuły iw ostatnim znaczeniu definicji podczas różnicowania.

Przy rozkładzie funkcji różniczkowania (wiedzy dawnej) można zapoznać się z listą innych przedsiębiorstw

Dla pierwszoplanowego przygotowania artyleryjskiego będzie mniej przerażających tyłków z wbudowanymi funkcjami 3-4-5. Możesz, jeśli nadepniesz na dwa tyłki, będziesz zbudowany jak figura składana, jeśli będziesz bardziej trzewny (lub cierpisz), to wszystko inne w rachunku różniczkowym stanie się dziecinne.

Tyłek 2

Poznaj utraconą funkcję

Jak miał na myśli, przy znanej podstawowej funkcji składania, konieczne jest prawidłowy ROZIBRATISYA przy depozycie. Na cichych vipadach, jeśli zgaduję, zgaduję cynamonowy priyom: bierzemy na przykład wartość „x” i próbujemy (myśli chi na czarno) umieścić tę wartość w „strasznym virazu”.

1) Musimy policzyć ilość virazów, suma to najlepsza inwestycja.

2) Następnie należy obliczyć logarytm:

4) Zmień cosinus na sześcian:

5) Na dole wzniesienia:

6) І, nareshty, najważniejszą funkcją jest pierwiastek kwadratowy:

Wzór na różniczkowanie funkcji składania zastosovayutsya w kolejności obrotowej, od funkcji samozwańczej do wewnętrznej. Wirishuumo:

Nachebto bez ułaskawienia:

1) Biorę to z pierwiastka kwadratowego.

2) wezmę to od ceny, zasady wikariusza

3) Istnieją trzy drogi do zera. Z kolejnego dodanku zabieram ze stopnia (kostkę).

4) biorę to z cosinusa.

6) Ja, nareshty, wezmę z najważniejszej inwestycji.

Możesz iść jeszcze ważniejsze, ale nadal nie najlepszy tyłek zwierzęcy. Zobacz na przykład kolekcję Kuznotsova i doceń całe piękno i prostotę różowej, dziecięcej. Kiedy się nad tym zastanowię, z przyjemnością położę się spać, zastanowić się, który umysł jest uczniem, jak wiem i odejdzie od funkcji składania, która nie jest uważna.

Ofensywny tyłek samodzielnego rozwiązania.

Tyłek 3

Poznaj utraconą funkcję

Pidkazka: Zbiór wspólnych zasad liniowości i zasada różnicowania do kreacji

Poza decyzją to jak lekcja.

Po nadejściu godziny, aby przejść do bardziej kompaktowych i uroczych chogo.
Nie śmieszna sytuacja, bo na tyłku nie ma dwóch, a trzy funkcje. Skąd mam wiedzieć, że wyjdę z trzech mnożników?

Tyłek 4

Poznaj utraconą funkcję

Jestem zdumiony, ale dlaczego nie da się przeliczyć trzech funkcji na dwie funkcje? Na przykład, jeśli w naszej pracy mamy dwa wyostrzenia, to możliwe jest stworzenie łuku krytycznego. Ale w zastosowaniu wszystkich funkcji rozwoju: kroków, wykładnika i logarytmu.

W takich przypadkach jest to konieczne w końcu zasosuvati zasada zróżnicowania wobec stwórcy dwa razy

Skupiamy się na fakcie, że s "y" są sensownie dwiema funkcjami: a th dla "ve" jest logarytmem:. Dlaczego możesz to zrobić? hiba - tse not tvir dwa mnożniki, a zasada nie jest praktyczna? Wyciszenie składane Nichogo:

Teraz jest w cieniu reguły na dziobie:

Nadal można się złościć i obwiniać za łuki, ale w tym przypadku można w takim widoku wyglądać piękniej - łatwiej zmienić.

Tyłek można oglądać w inny sposób:

Obraza drogi verishennya jest absolutnie słuszna.

Tyłek 5

Poznaj utraconą funkcję

Tyłek samodzielnego rozwiązania, jednocześnie pierwszy sposób.

Wyraźnie analogiczne niedopałki z frakcjami.

Tyłek 6

Poznaj utraconą funkcję

Tutaj możesz iść ścieżkami kіlkoma:

Dla tego:

Cała decyzja o spisaniu bardziej zwięźle, jak na pierwszym miejscu zasada zróżnicowania prywatnego , Przyjęte na cały dzień:

W zasadzie tyłek został pokazany, a jeśli zgubiłeś go w takim widoku, to nie będzie litości. Poza oczywistością, łatwo przełożyć to na czernety, ale dlaczego nie można tego wybaczyć?

Wskazując liczbę na spіlnomniki i dodaj ułamek o trzech wierzchołkach:

Minus dodatkovyh wybacza pole w tym, że є risik, aby uzyskać ułaskawienie już nie w znanym starym, ale w banalnych reinkarnacjach szkolnych. Z drugiej strony dziecku nie jest łatwo zbesztać pracownika i poprosić go, aby „doprowadził do końca” zgubionych.

Prosta kolba do samodzielnej rewizji:

Tyłek 7

Poznaj utraconą funkcję

Prodovzhumo opanowuje priyomię i wiedzę o nieprzyzwoitości i od razu typowe vipadoki są dostrzegalne, jeśli do różnicowania proponuje się „straszny” logarytm

Operacja czynienia różnicy nazywana jest różnicowaniem.

Wyniki rozwiązywania problemów związanych z wyprowadzeniem starych z najprostszych (a nawet prostszych) funkcji, wyznaczenie podobnych między wykonaniem przyrostu a poprawą argumentacji, podano tabelę starych definicji zasad. Isaac Newton (1643-1727) i Gotfrid Vilgelm Leibnits (1646-1716) jako pierwsi celebrowali stare.

Do tego w naszej godzinie chcę wiedzieć, czy będę należeć do funkcji, nie muszę zastanawiać się, jak odgadnąć różnicę między funkcją a argumentem, ale konieczne jest pozbawienie tabeli tych samych zasad różnicowania tak szybko, jak to możliwe. Po wiedzę najbiedniejszych przejdź do algorytmu ofensywnego.

będę wiedział, że pójdę, wymagaj viraz pod kreską powrót do magazynów z prostymi funkcjami tego rodzaju znaczenie, jak diyami (tvir, suma, prywatny) dzianiny i funkcja. Odległość dawnych funkcji elementarnych znana jest z tablic dawnych, a wzory dawnych, suma tych części - z reguł różniczkowania. Tabela starych i zasad różnicowania danych z pierwszych dwóch niedopałków.

zapas 1. Poznaj utraconą funkcję

Decyzja. 3 zasady różniczkowania z'yasovuєmo, które są tracone przez sumę funkcji є suma starych funkcji, tobto.

Z tabel starych, "xa" to stary, a stary sinus to cosinus. Na zakup pieniędzy z torby osoby starszej i oczywiście będę musiał ją otrzymać:

zapas 2. Poznaj utraconą funkcję

Decyzja. Zróżnicowanie pójdę do Sumi, w jakimś innym dodanok ze stałym mnożnikiem, co mogę winić za zły znak:

Gdy tylko znajdzie się jedzenie, gwiazdy zostaną zrobione, smród z reguły staje się wyraźniejszy, czytając tabelę starszych i najprostsze zasady różnicowania. Przed nimi mijam na raz.

Tabela starszych funkcji prostych

1. Wygląda jak stała (liczba). Czy to liczba (1, 2, 5, 200 ...), jak є w funkcji virazi. Ustaw drzwi na zero. Jeszcze ważniejsze jest to, aby pamiętać, że jest to konieczne jeszcze częściej
2. Pochіdna kwadratowa zimowa. Większość „Iksy”. Ustaw jednostkę drzwi. Tak ważne jest, aby zapamiętać nadovgo
3. Krok Pochidnej. Na krokach pierwszej godziny konieczne jest ożywienie budynku, aby odtworzyć pierwiastek niekwadratowy.
4. Wygląda jak zimowa w kroku -1
5. Jak pierwiastek kwadratowy
6. Szlak zatokowy
7. Możliwy cosinus
8. Na stycznej
9. Podobny do cotangensa
10. Podobny do arcsine
11. Podobny do arccosine
12. Jest podobny do arcus tangens
13. Wygląda na łuk cotangens
14. Podobny do logarytmu naturalnego
15. Przełączanie funkcji logarytmicznej
16. Wykładnik jest na wyświetlaczu
17. Funkcja pokazu chodzenia;

Zasady różnicowania

1. Pochіdna sumi chi rіznitsі
2. Idź, twórz
2a. Idzie virazi pomnożone przez stały mnożnik
3. Wygląda jak prywatny
4. Idealna funkcja składania

Zasada nr 1.Funkcje

różniczkowanie w niektórych punktach, a następnie w tych samych punktach różniczkowania i funkcji

w wyniku czego

Tobto. Suma funkcji algebraicznych poprzedniej sumy algebr starych funkcji jest tracona.

Ślizg. Ponieważ istnieją dwie funkcje, które różnicują, dostosuj się do starego dodatku, to stare, tobto.

Zasada 2Funkcje

zróżnicowane w punktach deyakiy, a następnie w tym samym punkcie zróżnicowane i

w wyniku czego

Tobto. Robot zostaje porwany z dwóch funkcji w celu stworzenia funkcji skóry do porwania robota.

Pasja 1. Stały mnożnik może być obwiniany za zły znak:

Pasja 2. Możesz stworzyć funkcje dekoracyjne, jak wyróżnić, zapewnić dużą ilość kreacji przestarzałego specjalisty od skóry dla nich wszystkich.

Na przykład dla trzech mnożników:

Zasada 3Funkcje

zróżnicowane w punktach deyakiy і , następnie w tym samym momencie jest różnicowana i prywatnieu / v, ponadto

Tobto. Prywatne dwie funkcje są stracone na rzecz ułamka drogowego, liczby є.

De scho shukati po innych stronach

W przypadku znanych, nieprzyzwoitych kreacji i części rzeczywistej kadry konieczne jest ustalenie od razu kilku zasad zróżnicowania, tym bardziej odnoszących się do starych - w statucie„Funkcje rzemieślnicze i prywatne”.

Szacunek. Przesunął się, aby nie oszukiwać stałej (tobto liczby) jako sumy pieniędzy i jako stałego mnożnika! Na vipadku dodanku її przegrywa się do zera, a w przypadku pojedynczego mnożnika wygrywa się winę za znak starego. Tse typowa pomilka, jak rozwijać się na etapie kolb wiwczenni starszych, ala w świecie odrodzenia tych samych jedno-dwupiętrowych tyłków średni uczeń przepraszam tsyu, bez względu na to, jak trudno jest.

A kiedy różnicujesz kreację prywatnego, masz dodanok ty"v w którym ty- liczba na przykład 2 lub 5, więc jest to stała, wtedy utracona liczba będzie wynosić zero, a wszystko to będzie zero (ten typ wyświetlania dla tyłka to 10).

nsha częste ułaskawienie- mechaniczne rozwiązanie podstawowych funkcji składania jako prostych funkcji prostych. Tomek funkcja chudego składania przypisane do artykułu. Trochę tego, co można łatwo poznać i zagubić proste funkcje.

Po drodze nie można obejść się bez rewizji viraz. Dla nich wszystkich krytyków można zobaczyć w nowych oknach serwisu Diy z krokami i korzeniamiі Diy z ułamkami .

Yaksho Vi shukte rozwiązanie starych ułamków w krokach i pierwiastkach, tobto, jeśli funkcją jest ma viglyad nachebto , a następnie przejdź do zajętego „Przejdź do sumy ułamków w krokach do pierwiastków”.

Cóż, przed tobą jest nachebto , to jesteś zajęty "Proste funkcje trygonometryczne Vyrobni".

Pokrokovi tyłek - skąd wiedzieć, że pójdę

zapas 3. Poznaj utraconą funkcję

Decyzja. Pierwsza część viraz funkcji to: cały viraz jest reprezentowany przez tvir, podobnie jak mnożniki - sumi, dla innych należy odjąć jeden z poprzednich mnożników. Istnieje ścisła zasada zróżnicowania tworzenia: stwórz dwie funkcje do tworzenia skóry z tymi samymi funkcjami dla starego:

Istnieje stała reguła różniczkowania sumi: suma funkcji algebraicznych poprzedniej sumy algebry starych funkcji cich jest tracona. Nasz vipad w skórze sumy ma jeszcze jeden dodatek ze znakiem minus. W przypadku galanterii skórzanej bachimo i zmiana samodzielna, które gubią się w niektórych kursach drogowych, a stała (liczba), giną na drogach takich jak zero. Otzhe, „ix” zmieniamy na jeden, a minus 5 - na zero. W innym viraz "ix" mnoży się przez 2, więc dwa razy mnoży się przez tę samą jednostkę, jak przejdę do "ix". Otrimuєmo te znaczenia starszych:

Umysł musi stracić wszystkie funkcje:

I można pogodzić zadanie rozwiązania problemu na koniec dnia.

zapas 4. Poznaj utraconą funkcję

Decyzja. Od nas konieczne jest poznanie zniknięcia prywatnego. Istnieje stały wzór na zróżnicowanie części: części dwóch funkcji są tracone w ułamku drogowym, liczba liczby є jest liczbą liczb zanikania normy, a normą jest kwadrat liczby liczb. Otrimuєmo:

Przejdę do mnożnika dla liczby i już znałem to w tyłku 2. Nie zapomniano też, że tvir, ale drugi mnożnik w tyłek przepływu jest przyjmowany ze znakiem minus:

Yaksho Vi shukєte rewizja takich budynków, dla tych, którzy muszą wiedzieć, stracę ich funkcje, de facto kupę korzeni i stopni, jak na przykład , to uprzejmie poproś o zajęty „Fakcje Virobna sumi w stopniach i korzeniach” .

Chcesz wiedzieć więcej o utraconych zatokach, cosinusach, tangensach i inshi funkcje trygonometryczne, tobto, jeśli funkcja to maє viglyad nachebto , to twoja lekcja "Proste funkcje trygonometryczne Virobni" .

Tyłek 5. Poznaj utraconą funkcję

Decyzja. W całej funkcji bachimo tvir, której jednym z mnożników jest pierwiastek kwadratowy niezależnej wędrówki, dawne były rozpoznawane w tabelach starszych. Zgodnie z zasadą różnicowania do stworzenia rozpoznana zostanie tabelaryczna wartość przestarzałego pierwiastka kwadratowego:

Możesz zmienić rozwiązanie zadań na ostatnie kalkulator online .

Tyłek 6. Poznaj utraconą funkcję

Decyzja. Funkcja jest prywatnie bachimo i jest pierwiastkiem kwadratowym z niezależnego krajobrazu. Kierując się zasadą różnicowania szeregowca, powtarzali, że tkwią w kolbie 4, że nie będzie dozwolone tabelaryczne znaczenie przestarzałego pierwiastka kwadratowego:

Schob strząsa ułamek w liczebniku, mnoży liczebnik i mianownik dalej.

Funkcja składanej przeglądarki, która zależy od funkcji funkcji składania. Ponieważ funkcja ma postać y = sin x - (2 - 3) a r c t g x x 5 7 x 10 - 17 x 3 + x - 11, to nie można jej złożyć do widoku jako y = sin 2 x.

Artykuł pokaże zrozumienie funkcji składania i wyglądu. Poprawione formułami znakhozhennya pohіdnoї, jeśli kolby zmartwychwstałego w visnovku. Zastój na starych stołach i zasady różnicowania można zmienić, aby zmienić godzinę na stare.

Główne wartości

Wartość biznesowa 1

Funkcja składania jest używana dla takiej funkcji, ponieważ argument jest również funkcją.

To oznacza tse w ten sposób: f (g (x)). Mamo, że funkcja g (x) jest zaangażowana w argument f (g (x)).

Wartość biznesowa 2

Ponadto funkcją jest f i jest funkcją cotangensa, więc g (x) = ln x jest całą funkcją logarytmu naturalnego. Zdajemy sobie sprawę, że funkcję składania f (g (x)) można zapisać jako arctan (lnx). Aby funkcja f, która jest funkcją 4 kroków, de g (x) = x 2 + 2 x - 3 była używana jako cała funkcja wymierna, możemy zaprzeczyć, że f (g (x)) = (x 2 + 2 x - 3) 4 .

Oczywiście g (x) można złożyć. Z dolnika y = sin 2 x + 1 x 3 - 5 widać, że wartość g maє korzeń sześcienny s frakcja. Daniy viraz można zdefiniować jako y = f (f 1 (f 2 (x))). Gwiazdy to mamo, f to funkcja sinus, a f 1 to funkcja, którą można przekształcić w pierwiastek kwadratowy, f 2 (x) = 2 x + 1 x 3 - 5 jest funkcją wymierną strzału.

Wartość biznesowa 3

Krok wkładu ma być liczbą naturalną i zapisać jako y = f (f 1 (f 2 (f 3 (... (F n (x))))))))).

Wartość biznesowa 4

Zrozumienie składu funkcji należy odnieść do liczby wkładów w umysł. Po raz pierwszy rozważany jest wzór na znajomość funkcji składania chudego

(f (g (x))) "= f" (g (x)) g "(x)

Włączać

Tyłek 1

Poznaj utraconą funkcję składania w postaci y = (2 x + 1) 2.

Decyzja

Po przemyciu jest jasne, że f jest funkcją kwadratową, a g (x) = 2 x + 1 jest używane jako funkcja liniowa.

Istnieje bardzo powszechna formuła funkcji składania, którą można zapisać:

f "(g(x)) = ((g (x)) 2)" = 2 · (g (x)) 2 - 1 = 2 · g (x) = 2 · (2 ​​x + 1); g "(x) = (2 x + 1)" = (2 x) "+ 1" = 2 x "+ 0 = 2 1 x 1 - 1 = 2 ⇒ (f (g (x))) "= f " (g (x)) g "(x) = 2 (2 x + 1) 2 = 8 x + 4

Konieczne jest poznanie utraconych z wybaczeniem zewnętrznego spojrzenia na funkcję. Otrimuєmo:

y = (2 x + 1) 2 = 4 x 2 + 4 x + 1

Zvidsi maєmo, scho

y "= (4 x 2 + 4 x + 1)" = (4 x 2) "+ (4 x)" + 1 "= 4 · (x 2)" + 4 · (x) "+ 0 = = 4 2 x 2 - 1 + 4 1 x 1 - 1 = 8 x + 4

Wyniki zostały punktowane.

Podczas oglądania tego typu roślin ważne jest, aby zrozumieć funkcję de roztashovuvatyuvati postaci f і g (x).

Tyłek 2

Przesuń, aby poznać stare funkcje składania postaci y = sin 2 x i y = sin x 2.

Decyzja

Pierwszą funkcją, która zapisuje funkcję, jest redukcja, ale f jest funkcją kwadratową, a g (x) jest funkcją sinus. Todi otrimaєmo, scho

y "= (sin 2 x)" = 2 grzech 2 - 1 x (sin x) "= 2 grzech x cos x

Inny zapis pokazuje, że f jest funkcją sinus, a g (x) = x 2 to funkcja stanu... Zvidsy vipliv

y "= (sin x 2)" = cos (x 2) (x 2) "= cos (x 2) 2 x 2 - 1 = 2 x cos (x 2)

Wzór na proste y = f (f 1 (f 2 (f 3 (... (Fn (x)))))))) jest zapisany jako y "= f" (f 1 (f 2 (f 3 ( .. .) fn (x)))))) f 1 "(f 2 (f 3 (... (fn (x)))))) f 2" (f 3 (... (fn ( x) ))))) ... ... · F n "(x)

Tyłek 3

Poznaj utraconą funkcję y = sin (ln 3 a r c t g (2 x)).

Decyzja

Duńska kolba pokaże składalność płyty i oznaczenie funkcji rozet. Todi y = f (f 1 (f 2 (f 3 (f 4 (x)))))), de f, f 1, f 2, f 3, f 4 (x) jest funkcją sinus, funkcją 3 kroki, funkcja logarytmu to podstawa e, funkcja to arcus tangens i prosta.

3 wzory na wartość funkcji składania maєmo, scho

y "= f" (f 1 (f 2 (f 3 (f 4 (x))))) f 1 "(f 2 (f 3 (f 4 (x))))) f 2" ( f 3 ( f 4 (x))) f 3 "(f 4 (x)) f 4" (x)

Otrimuєmo, jak wiedzieć

1. f „(f 1 (f 2 (f 3 (f 4 (x)))))) jako sinus jest odprowadzony zgodnie z tabelami starszych, do f” (f 1 (f 2 (f 3 (f 4 (f)) x))))) ) = cos (ln 3 arctan (2 x)).
2. f 1 "(f 2 (f 3 (f 4 (x)))) Przyjmę funkcję stanu, więc f 1" (f 2 (f 3 (f 4 (x)))) = 3 ln 3 - 1 arctan (2 x) = 3 ln 2 arctan (2 x).
3. f 2 "(f 3 (f 4 (x))) jest logarytmiczne, więc f 2" (f 3 (f 4 (x))) = 1 a r c t g (2 x).
4. f 3 "(f 4 (x)) jako starszy arcus tangens, toodi f 3" (f 4 (x)) = 1 1 + (2 x) 2 = 1 1 + 4 x 2.
5. Przy znanym złym f 4 (x) = 2 x śmierć 2 dla złego znaku złej statystyki ze wskaźnika, który jest drogi 1 do f 4 "(x) = (2 x)" = 2 x "= 2 · 1 x 1 - 1 = 2.

Przeprowadzenie integracji wyników pośrednich, które zostaną rozpoznane,

y "= f" (f 1 (f 2 (f 3 (f 4 (x))))) f 1 "(f 2 (f 3 (f 4 (x))))) f 2" ( f 3 ( f 4 (x))) f 3 "(f 4 (x)) f 4" (x) = = cos (ln 3 arctan (2 x)) 3 ln 2 arctan (2 x) 1 arctan (2 x) 1 1 + 4 x 2 2 = = 6 cos (ln 3 arctan (2 x)) ln 2 arctan (2 x) arctan (2 x) (1 + 4 x 2 )

Wybór takich funkcji matrioszki nagadu. Nie oczekuje się, że zasady różnicowania utkną w oczywiste czujność na dodatkowe stoły starszych. Najczęściej konieczne jest ustalenie wzoru na znajomość starych funkcji składania.

Zobacz, jak wyglądają funkcje składania. Przy wyraźnym poczuciu rozwoju wiedza o starości jest szczególnie łatwa.

Tyłek 4

Trzeba przyjrzeć się celowaniu takiego tyłka. Ponieważ jest to funkcja postaci y = t g 2 x + 3 t g x + 1, to można przyjrzeć się postaci złożonej g (x) = t g x, f (g) = g 2 + 3 g + 1. Oczywiście konieczne jest znalezienie wzoru na składany nieznośny:

f "(g (x)) = (g 2 (x) + 3 g (x) + 1)" = (g 2 (x)) "+ (3 g (x))" + 1 "= = 2 · g 2 - 1 (x) + 3 · g "(x) + 0 = 2 g (x) + 3 · 1 · g 1 - 1 (x) = = 2 g (x) + 3 = 2 tgx + 3; g "(x) = (tgx)" = 1 cos 2 x ⇒ y "= (f (g (x)))" = f "(g (x)) g" (x) = (2 tgx + 3 ) 1 cos 2 x = 2 tgx + 3 cos 2 x

Funkcja postaci y = t g x 2 + 3 t g x + 1 nie mieści się w składanych fragmentach sumy t g x 2 3 t g x і 1. Jednak t g x 2 pasuje do funkcji składania, wtedy możemy przyjąć funkcję stanu jako g (x) = x 2 і f є funkcja styczna. Za cały slajd zróżnicowania torby. Otrimuєmo, scho

y „= (tgx 2 + 3 tgx + 1)” = (tgx 2) „+ (3 tgx)” + 1 „= = (tgx 2)” + 3 · (tgx) „+ 0 = (tgx 2)” + 3 co 2 x

Przechodzimy do znanej podstawowej funkcji składania (t g x 2) ”:

f "(g (x)) = (tan (g (x)))" = 1 cos 2 g (x) = 1 cos 2 (x 2) g "(x) = (x 2)" = 2 x 2 - 1 = 2 x ⇒ (tgx 2) "= f" (g (x)) g "(x) = 2 x cos 2 (x 2)

Możemy rozpoznać, że y „= (t g x 2 + 3 t g x + 1)” = (t g x 2) „+ 3 cos 2 x = 2 x cos 2 (x 2) + 3 cos 2 x

Funkcje składania można uwzględnić przed magazynem funkcji składania, a same funkcje składania mogą być funkcjami składania.

Tyłek 5

Aplikacja może być łatwo zwijana w postaci y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x (x 2 + 1)

Funkcję tę można przedstawić za pomocą widoku y = f (g (x)), co oznacza, że ​​f jest funkcją logarytmu w podzbiorze 3, a g (x) może być użyte jako suma dwóch funkcji postaci h (x ) = x 2 + 3 cos 3 (2 x + 1) + 7 ex 2 + 3 3 w k (x) = ln 2 x (x 2 + 1). Oczywiście y = f (h (x) + k (x)).

Funkcja h(x) jest zrozumiała. Cena l (x) = x 2 + 3 cos 3 (2 x + 1) + 7 do m (x) = e x 2 + 3 3

Mahmo, l (x) = x 2 + 3 cos 2 (2 x + 1) + 7 = n (x) + p (x) є suma dwóch funkcji n (x) = x 2 + 7 i p (x ) = 3 cos 3 (2 x + 1), de p (x) = 3 p 1 (p 2 (p 3 (x))) jest funkcją składania z funkcją numeryczną 3 i p 1 jest funkcją redukcji do sześcian, p 2 funkcja cosinus, p 3 (x) = 2 x + 1 jest funkcją liniową.

Gdyby m (x) = ex 2 + 3 3 = q (x) + r (x) є suma dwóch funkcji q (x) = ex 2 і r (x) = 3 3 de q (x) = q 1 (q 2 (x)) jest funkcją składania, q 1 jest funkcją wykładniczą, q 2 (x) = x 2 jest funkcją stanu.

Można zauważyć, że h (x) = l (x) m (x) = n (x) + p (x) q (x) + r (x) = n (x) + 3 p 1 (p 2 ( p 3 (x))) q 1 (q 2 (x)) + r (x)

Przechodząc do virazu postaci k (x) = ln 2 x (x 2 + 1) = s (x) 1 (s 2 (x)) z całym wymiernym t (x) = x 2 + 1, de s 1 jest funkcją kwadratową, a s 2 (x) = ln x jest podstawą logarytmiczną e.

Wygląda jak mrugnięcie, więc możesz zobaczyć k (x) = s (x) t (x) = s 1 (s 2 (x)) t (x).

Todi otrimaєmo, scho

y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 ex 2 + 3 3 + ln 2 x (x 2 + 1) = = fn (x) + 3 p 1 (p 2 (p 3 ( x))) q 1 (q 2 (x)) = r (x) + s 1 (s 2 (x)) t (x)

Za strukturami funkcji stało się jasne, że formuły muszą zostać ustalone, aby łatwiej było zwrócić się o to zróżnicowanie. Aby poznać pozostałe budynki i zrozumieć ich transmisję, należy zwrócić się do punktu zróżnicowania funkcji, aby poznać tę najzabawniejszą.

Yaksho Vi zaznaczył ułaskawienie w tekście, bądź łasica, patrz i natisnit Ctrl + Enter

Pierwsze twierdzenie o utraconej funkcji składania, którego wzór jest następujący:

Idź 1) funkcja $ u = \ varphi (x) $ może być użyta do uzyskania $ u_ (x) "= \ varphi" (x_0) $; 2) funkcja $ y = f (u) $ może być użyta w tych samych punktach $ u_0 = \ varphi (x_0) $ będzie potrzebna $ y_ (u) "= f" (u) $. Todi składana funkcja $ y = f \ left (\ varphi (x) \ right) $ w zgadywanych punktach też stracę to samo, dodam kilka starszych funkcji $ f (u) $ i $ \ varphi (x) $ :

$$ \ left (f (\ varphi (x)) \ right) "= f_ (u)" \ left (\ varphi (x_0) \ right) \ cdot \ varphi "(x_0) $$

Ale w większej krótkiej notacji: $ y_ (x) "= y_ (u)" \ cdot u_ (x) "$.

Na krańcach tego samego rozkładu wszystkie funkcje można zobaczyć w postaci $ y = f (x) $ (tak, że widoczna jest tylko jedna zmienna funkcja $ x $). Najwyraźniej wszystkie akcje mają zmianę $ y "$ sprzęt $ x $.

Na kolbach nr 1, nr 2 i nr 3 przeprowadzono proces raportowania funkcji składania zakhozhennya pohіdnoї. Załącznik nr 4 wskazuje na większą czytelność tabel starszych i bardziej sensownych.

Materiał Bazhano pislya vivchennya w zapasach nr 1-3 przechodzi do niezależnego rozwiązania zapasów nr 5, nr 6 i nr 7. Zastosuj nr 5, nr 6 i nr 7 do krótkiego rozwiązania, aby czytelnik mógł ponownie rozważyć poprawność swojego wyniku.

Tyłek numer 1

Poznaj utraconą funkcję $ y = e ^ (\ cos x) $.

Musimy znać utraconą funkcję składania $ y "$. Oscylacje $ y = e ^ (\ cos x) $, a następnie $ y" = \ lewo (e ^ (\ cos x) \ prawo) "$. lewo (e ^ (\ cos x) \ right) "wzór $ vikora nr 6 z tabel starszych. Przy okazji, formuła nr 6 jest wymagana, ale w naszym przypadku $ u = \ cos x $. Dalsze rozwiązanie pola przy banalnej instalacji formuły #6 viraz $ \ cos x $ replace $ u $:

$$ y "= \ left (e ^ (\ cos x) \ right)" = e ^ (\ cos x) \ cdot (\ cos x) "\ tag (1.1) $$

Teraz konieczne jest poznanie wartości viraz $ (\ cos x) "$. Znam bestię do tabeli starszych, wybierana jest z niej formuła nr 10. Możesz podać $ u = x $ dla formuła nr 10, ale: $ (\ cos x)" = - \ sin x \ cdot x "$. Teraz parzystość (1.1) jest kontynuowana, dodając następujący wynik:

$$ y "= \ left (e ^ (\ cos x) \ right)" = e ^ (\ cos x) \ cdot (\ cos x) "= e ^ (\ cos x) \ cdot (- \ sin x \ cdot x ") \ tag (1.2) $$

Oscylacje $ x "= 1 $, to parzystość (1.2) jest kontynuowana:

$$ y "= \ left (e ^ (\ cos x) \ right)" = e ^ (\ cos x) \ cdot (\ cos x) "= e ^ (\ cos x) \ cdot (- \ sin x \ cdot x ") = e ^ (\ cos x) \ cdot (- \ sin x \ cdot 1) = - \ sin x \ cdot e ^ (\ cos x) \ tag (1.3) $$

Otzhe, zgodnie z (1.3), maєmo: $ y "= - \ sin x \ cdot e ^ (\ cos x) $. 1.3) Otzhe, funkcja składania została utracona, została pozbawiona pozbawienia nagranie.

Pogląd: $ y "= - \ sin x \ cdot e ^ (\ cos x) $.

Tyłek numer 2

Poznaj utraconą funkcję $ y = 9 \ cdot \ arctg ^ (12) (4 \ cdot \ ln x) $.

Musimy policzyć utracone $ y "= \ left (9 \ cdot \ arctg ^ (12) (4 \ cdot \ ln x) \ right)" $. Jest całkiem jasne, że za zły znak można winić stałą (czyli liczbę 9):

$$ y "= \ left (9 \ cdot \ arctg ^ (12) (4 \ cdot \ ln x) \ right)" = 9 \ cdot \ left (\ arctg ^ (12) (4 \ cdot \ ln x) \ prawo) "\ tag (2.1) $$

Teraz, wirusowo, $ \ left (\ arctg ^ (12) (4 \ cdot \ ln x) \ right) "$. Jeśli chcesz wibrować, będę potrzebować łatwiej formuły ze starych tabel, będę przedstawiam viraz, jak wyglądać w takim widoku: $ \ left (\ left (\ arctg (4 \ cdot \ ln x) \ right) ^ (12) \ right) "$. Teraz jest jasne, że konieczne jest vikoristovuvati formuła nr 2, tobto. $ \ left (u ^ \ alpha \ right) "= \ alpha \ cdot u ^ (\ alpha-1) \ cdot u" $. Formuła jest reprezentowana przez $ u = \ arctg (4 \ cdot \ ln x) $ і $ \ alpha = 12 $:

Dodatkowa równość (2.1) jest odejmowana od wyniku, maєmo:

$$ y "= \ left (9 \ cdot \ arctg ^ (12) (4 \ cdot \ ln x) \ right)" = 9 \ cdot \ left (\ arctg ^ (12) (4 \ cdot \ ln x) \ right) "= 108 \ cdot \ left (\ arctg (4 \ cdot \ ln x) \ right) ^ (11) \ cdot (\ arctg (4 \ cdot \ ln x))" \ tag (2.2) $$

W takiej sytuacji ułaskawienie jest często dozwolone, jeśli po raz pierwszy wybierzesz formułę $ (\ arctg \; u) "= \ frac (1) (1 + u ^ 2) \ cdot u" $ zastąp formuły $ \ left (u ^ \ alpha \ right) "= \ alpha \ cdot u ^ (\ alpha-1) \ cdot u" $. Po prawej pierwszy odpowiada za pierwotną funkcję. Spójrz na to, ponieważ sama funkcja przyda się do rzutowania $ \ arctg ^ (12) (4 \ cdot 5 ^ x) $, zobacz czy używasz wartości $ \ arctg ^ (12) (4 \ cdot 5 ^ x) $, dla którego wartość wynosi $ x $. Użyj małego wyboru wartości $ 5 ^ x $, a następnie pomnóż wynik przez 4, odcinając $ 4 \ cdot 5 ^ x $. Od teraz arcus tangens jest pobierany z wyniku po usunięciu $ arctg (4cdot 5 ^ x) $. Następnie liczbę można zredukować do dwunastu kroków, co można przedstawić jako $ arctg (12) (4 cdot 5 x) $. Zatrzymaj dia - tobto. Budynek w kroku 12 będzie miał świetną funkcję. Pierwszą rzeczą do zrobienia jest naprawienie starego, ale jest zepsute przez zapał (2.2).

Teraz musisz znać $ (\ arctg (4 \ cdot \ ln x)) "$. Formuła Victora nr 19 starszych tabel, po umieszczeniu w niej $ u = 4 \ cdot \ ln x $:

$$ (\ arctg (4 \ cdot \ ln x)) "= \ frac (1) (1+ (4 \ cdot \ ln x) ^ 2) \ cdot (4 \ cdot \ ln x)" $$

Trójki można łatwo usunąć z viraz, a o $ (4 \ cdot \ nn x) ^ 2 = 4 ^ 2 \ cdot (\ ln x) ^ 2 = 16 \ cdot \ ln ^ 2 x $.

$$ (\ arctg (4 \ cdot \ ln x)) "= \ frac (1) (1+ (4 \ cdot \ ln x) ^ 2) \ cdot (4 \ cdot \ ln x)" = \ frac ( 1) (1 + 16 \ cdot \ ln ^ 2 x) \ cdot (4 \ cdot \ ln x) "$$

Równość (2.2) wygląda teraz następująco:

$$ y "= \ left (9 \ cdot \ arctg ^ (12) (4 \ cdot \ ln x) \ right)" = 9 \ cdot \ left (\ arctg ^ (12) (4 \ cdot \ ln x) \ right) "= \\ = 108 \ cdot \ left (\ arctg (4 \ cdot \ ln x) \ right) ^ (11) \ cdot (\ arctg (4 \ cdot \ ln x))" = 108 \ cdot \ left (\ arctg (4 \ cdot \ ln x) \ right) ^ (11) \ cdot \ frac (1) (1 + 16 \ cdot \ ln ^ 2 x) \ cdot (4 \ cdot \ ln x) " \ tag (2.3) $$

Jest już za późno, aby poznać $ (4 \ cdot \ ln x) "$. Czyli stała (tobto 4) dla złego znaku: $ (4 \ cdot \ ln x)" = 4 \ cdot (\ ln x) "$ $ (\ ln x) "$ vikoristymo formuła nr 8, wkładając w nią $ u = x $: $ (\ ln x)" = \ frac (1) (x) \ cdot x "$. Oskilki $ x "= 1 $, to $ (\ ln x)" = \ frac (1) (x) \ cdot x "= \ frac (1) (x) \ cdot 1 = \ frac (1) (x) $ Składając odrzucenie wyniku do wzoru (2.3), możemy wywnioskować:

$$ y "= \ left (9 \ cdot \ arctg ^ (12) (4 \ cdot \ ln x) \ right)" = 9 \ cdot \ left (\ arctg ^ (12) (4 \ cdot \ ln x) \ right) "= \\ = 108 \ cdot \ left (\ arctg (4 \ cdot \ ln x) \ right) ^ (11) \ cdot (\ arctg (4 \ cdot \ ln x))" = 108 \ cdot \ left (\ arctg (4 \ cdot \ ln x) \ right) ^ (11) \ cdot \ frac (1) (1 + 16 \ cdot \ ln ^ 2 x) \ cdot (4 \ cdot \ ln x) " = \\ = 108 \ cdot \ left (\ arctg (4 \ cdot \ ln x) \ right) ^ (11) \ cdot \ frac (1) (1 + 16 \ cdot \ ln ^ 2 x) \ cdot 4 \ cdot \ frac (1) (x) = 432 \ cdot \ frac (\ arctg ^ (11) (4 \ cdot \ ln x)) (x \ cdot (1 + 16 \ cdot \ ln ^ 2 x)). $

Domyślam się, że funkcja składania najczęściej znajduje się w jednym rzędzie - tak jak jest napisane w ostatnim rimnosti. Oznacza to, że podczas formalizowania standardowych projektów lub sterowania robotami nie jest konieczne tak szczegółowe opisywanie rozwiązania.

Pogląd: $ y "= 432 \ cdot \ frac (\ arctg ^ (11) (4 \ cdot \ ln x)) (x \ cdot (1 + 16 \ cdot \ ln ^ 2 x)) $.

Tyłek nr 3

Poznaj $ y "$ funkcje $ y = \ sqrt (\ sin ^ 3 (5 \ cdot9 ^ x)) $.

W przypadku kolby składającej się z trzech zmień funkcję $ y $, przechwytując pierwiastek (pierwotny) widoku schodkowego: $ y = \ sqrt (\ sin ^ 3 (5 \ cdot9 ^ x)) = \ left (\ sin ( 5 \ cdot 9 ^ x) \ prawo) ^ (\ frac (3) (7)) $. Teraz zacznie się do wczesnych dni. Oskilki $ y = \ lewo (\ sin (5 \ cdot 9 ^ x) \ prawo) ^ (\ frac (3) (7)) $, to:

$$ y "= \ lewo (\ lewo (\ sin (5 \ cdot 9 ^ x) \ prawo) ^ (\ frac (3) (7)) \ prawo)" \ tag (3.1) $$

Formuła Victora nr 2 z tabel starszych, po umieszczeniu w niej $ u = \ sin (5 \ cdot 9 ^ x) $ і $ \ alpha = \ frac (3) (7) $:

$$ \ left (\ left (\ sin (5 \ cdot 9 ^ x) \ right) ^ (\ frac (3) (7)) \ right) "= \ frac (3) (7) \ cdot \ left ( \ sin (5 \ cdot 9 ^ x) \ prawo) ^ (\ frac (3) (7) -1) (\ sin (5 \ cdot 9 ^ x)) "= \ frac (3) (7) \ cdot \ lewo (\ sin (5 \ cdot 9 ^ x) \ prawo) ^ (- \ frac (4) (7)) (\ sin (5 \ cdot 9 ^ x)) "$$

Ciągle równy (3.1), wynik jest następujący:

$$ y "= \ lewo (\ lewo (\ sin (5 \ cdot 9 ^ x) \ prawo) ^ (\ frac (3) (7)) \ prawo)" = \ frac (3) (7) \ cdot \ left (\ sin (5 \ cdot 9 ^ x) \ right) ^ (- \ frac (4) (7)) (\ sin (5 \ cdot 9 ^ x)) "\ tag (3.2) $$

Teraz trzeba znać $ (\ sin (5 \ cdot 9 ^ x)) "$. Vikoristovu dla tej formuły nr 9 z tabel starszych, po umieszczeniu w niej $ u = 5 \ cdot 9 ^ x $ :

$$ (\ sin (5 \ cdot 9 ^ x)) "= \ cos (5 \ cdot 9 ^ x) \ cdot (5 \ cdot 9 ^ x)" $$

Po poprawieniu parzystości (3.2) zaprzeczamy jednak wynikowi:

$$ y "= \ lewo (\ lewo (\ sin (5 \ cdot 9 ^ x) \ prawo) ^ (\ frac (3) (7)) \ prawo)" = \ frac (3) (7) \ cdot \ left (\ sin (5 \ cdot 9 ^ x) \ right) ^ (- \ frac (4) (7)) (\ sin (5 \ cdot 9 ^ x)) "= \\ = \ frac (3) (7) \ cdot \ lewy (\ sin (5 \ cdot 9 ^ x) \ prawy) ^ (- \ frac (4) (7)) \ cos (5 \ cdot 9 ^ x) \ cdot (5 \ cdot 9 ^ x) "\ tag (3.3) $$

Było za późno, aby poznać $ (5 \ cdot 9 ^ x) "$. W przypadku kolby potrzebujemy stałej (liczba $ 5 $) dla złego znaku, więc $ (5 \ cdot 9 ^ x)" = 5 \ cdot (9 ^ x) "$. Dla znanego starego $ (9 ^ x) "$ użyjesz formuły nr 5 starych tabel, po złożeniu do niej $ a = 9 $ і $ u = x $: $ (9 ^ x)" = 9 ^ x \ cdot \ ln9 \ cdot x "$. Oscylacje $ x "= 1 $, potem $ (9 ^ x)" = 9 ^ x \ cdot \ ln9 \ cdot x "= 9 ^ x \ cdot \ ln9 $. Teraz możemy kontynuować równość (3.3):

$$ y "= \ lewo (\ lewo (\ sin (5 \ cdot 9 ^ x) \ prawo) ^ (\ frac (3) (7)) \ prawo)" = \ frac (3) (7) \ cdot \ left (\ sin (5 \ cdot 9 ^ x) \ right) ^ (- \ frac (4) (7)) (\ sin (5 \ cdot 9 ^ x)) "= \\ = \ frac (3) (7) \ cdot \ lewy (\ sin (5 \ cdot 9 ^ x) \ prawy) ^ (- \ frac (4) (7)) \ cos (5 \ cdot 9 ^ x) \ cdot (5 \ cdot 9 ^ x) "= \ frac (3) (7) \ cdot \ po lewej (\ sin (5 \ cdot 9 ^ x) \ po prawej) ^ (- \ frac (4) (7)) \ cos (5 \ cdot 9 ^ x) \ cdot 5 \ cdot 9 ^ x \ cdot \ ln9 = \\ = \ frac (15 \ cdot \ ln 9) (7) \ cdot \ left (\ sin (5 \ cdot 9 ^ x) \ right) ^ (- \ frac (4) (7)) \ cdot \ cos (5 \ cdot 9 ^ x) \ cdot 9 ^ x. $$

Możesz ponownie przejść od kroków do radykałów (być korzeniem), wpisując $ \ left (\ sin (5 \ cdot 9 ^ x) \ right) ^ (- \ frac (4) (7)) $ w przeglądarka $ \ frac (1 ) (\ left (\ sin (5 \ cdot 9 ^ x) \ right) ^ (\ frac (4) (7))) = \ frac (1) (\ sqrt (\ sin ^ 4 (5 \) cdot 9 ^ x))) $. Todi zostanie napisane w następującej formie:

$$ y "= \ frac (15 \ cdot \ ln 9) (7) \ cdot \ left (\ sin (5 \ cdot 9 ^ x) \ right) ^ (- \ frac (4) (7)) \ cdot \ cos (5 \ cdot 9 ^ x) \ cdot 9 ^ x = \ frac (15 \ cdot \ ln 9) (7) \ cdot \ frac (\ cos (5 \ cdot 9 ^ x) \ cdot 9 ^ x) (\ sqrt (\ sin ^ 4 (5 \ cdot 9 ^ x))). $$

Pogląd: $ y "= \ frac (15 \ cdot \ ln 9) (7) \ cdot \ frac (\ cos (5 \ cdot 9 ^ x) \ cdot 9 ^ x) (\ sqrt (\ sin ^ 4 (5 \ ) cdot 9 ^ x))) $.

Tyłek nr 4

Pokaż, że formuła nr 3 i nr 4 tabeli starszej є okremiy formuły nr 2 tabeli.

Formuła nr 2 tabel starszych ma tę samą funkcję $ u ^ \ alpha $. Dla formuły nr 2 podajemy $\alpha = -1 $, możemy rozpoznać:

$$ (u ^ (- 1)) "= - 1 \ cdot u ^ (- 1-1) \ cdot u" = - u ^ (- 2) \ cdot u "\ tag (4.1) $$

Oscylacje $ u ^ (- 1) = \ frac (1) (u) $ і $ u ^ (- 2) = \ frac (1) (u ^ 2) $, to równość (4.1) można przepisać w następujący sposób: $ \ left (\ frac (1) (u) \ right) "= - \ frac (1) (u ^ 2) \ cdot u" $. Tse і є formuła nr 3 tabele starszych.

Znam bestie do formuły nr 2 w tabelach starszych. Rozszerzalnie $ \ alpha = \ frac (1) (2) $:

$$ \ left (u ^ (\ frac (1) (2)) \ right) "= \ frac (1) (2) \ cdot u ^ (\ frac (1) (2) -1) \ cdot u" = \ frac (1) (2) u ^ (- \ frac (1) (2)) \ cdot u "\ tag (4.2) $$

Oskilki $ u ^ (\ frac (1) (2)) = \ sqrt (u) $ і $ u ^ (- \ frac (1) (2)) = \ frac (1) (u ^ (\ frac (1 ) (2))) = \ frac (1) (\ sqrt (u)) $, to parzystość (4.2) można przepisać w następujący sposób:

$$ (\ sqrt (u)) "= \ frac (1) (2) \ cdot \ frac (1) (\ sqrt (u)) \ cdot u" = \ frac (1) (2 \ sqrt (u) ) \ cdot u "$$

Parzystość Otrimana $ (sqrt (u)) "= \ frac (1) (2sqrt (u)) cdot u" $ і formuła nr 4 tabele starszych. Yak bachite, formuły nr 3 i nr 4 tabele starszych przechodzą od formuły nr 2 do ustawienia $ alfa $.