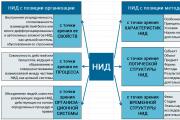
Linearna zmota vektorja je osnova odločitve. Linearno neodvisni in linearno neodvisni vektorji
Vektorji, njihova moč in dії z njimi
Vektorji, dії z vektorji, linearni vektorski prostor.
Zaporedje končnih števil je vektorsko urejeno.
Dії: 1. Množenje vektorja s številom: lambda * vektor x \u003d (lamda * x 1, lambda * x 2 ... lambda * x n). (3.4, 0. 7) * 3 = (9, 12,0.21 )
2. Zložljivi vektorji (da ležijo na istem vektorskem prostoru) vektor x + vektor y \u003d (x 1 + y 1, x 2 + y 2, ... x n + y n,)
3. Vektor 0=(0,0…0)---n E n – n-dimenzionalni (linearni prostor) vektor x + vektor 0 = vektor x
Izrek. Da bi bil sistem n vektorjev, n-svetovni linearni prostor linearno zapuščen, je potrebno in zadostno, da bo eden od vektorjev linearna kombinacija drugih.
Izrek. Be-yaka sukupnіst n+ 1. vektor n-svetovno linearno prostranstvo yavl. linearna ledina.
Seštevanje vektorjev, množenje vektorjev s številkami. Vіdnіmannya vektorіv.
Vsota dveh vektorjev se imenuje vektor, ki se izravna od storža vektorja do konca vektorja, saj mislimo, da je storž od konca vektorja. Tako kot so vektorji nastavljeni s svojimi postavitvami glede na vektorje osnovne enote, se pri zlaganju vektorjev dodajo njihove ustrezne koordinate.
Poglejmo si primer kartezijanskega koordinatnega sistema. daj no
Pokažimo kaj
Z baby 3 to lahko vidite ![]()

Vsoto poljubnega končnega števila vektorjev najdemo za pravilom bagatokutnika (slika 4): da induciramo vsoto končnega števila vektorjev, je dovolj, da vzamemo uho kožno ofenzivnega vektorja z konca sprednjega in induciramo vektor, ki gre za uho prvega vektorja s koncem ostalega.

Moč operacije zlaganja vektorjev:
V cich virase m so n številke.
Razliki vektorjev pravimo vektor, drugi dodatni vektor pa je vektor, protilni vektor za ravno črto, vendar enak drugemu.

Na ta način se operacijo premikanja vektorja nadomesti z operacijo zlaganja
Vektor, katerega storž se nahaja na storžu koordinat, in konec - v točki A (x1, y1, z1), se imenuje vektor polmera točke A i ali preprosto. Delci jogo koordinat so premaknjeni od koordinat točke A, vidna je razporeditev jogo vzdolž vektorjev
Vektor, ki se lahko začne v točki A(x1, y1, z1) in konča v točki B(x2, y2, z2) ![]()
de r 2 - vektor polmera točke; r 1 je vektor polmera točke A.
Zato je mogoče videti postavitev vektorja v smislu vektorjev
Yogo dozhina je lepša med točkama A in B
MNOŽITE
Torej, v primeru ploščatih problemov je dodatek vektorja na a = (ax; ay) številu b za formulo
a b = (ax b; ay b)
Primer 1. Poiščite prirast vektorja a = (1; 2) za 3.
3 a = (3 1; 3 2) = (3; 6)
Torej, v primeru prostorskega problema je povečanje vektorja a = (ax; ay; az) za število b za formulo
a b = (ax b; ay b; az b)
Primer 1. Poiščite prirast vektorja a = (1; 2; -5) za 2.
2 a = (2 1; 2 2; 2 (-5)) = (2; 4; -10)
Skalarni dobootok vector_v to ![]() de - Rez med vektorji i; yakscho abo, torej
de - Rez med vektorji i; yakscho abo, torej
Z vidika skalarnega ustvarjanja to kričiš ![]()
de, na primer, ê vrednost projekcije vektorja neposredno na vektor .
Skalarni kvadratni vektor:
Moč skalarnega ustvarjanja:
![]()
![]()
![]()
![]()
Skalarni twir v koordinatah
Yakscho ![]()
![]() potem
potem ![]()
Kut mizh vektorji
Rezi med vektorji – reži med ravnimi črtami med vektorji (najmanjši rez).
Vector TV (Vektorska TV dveh vektorjev) tse psevdovektor, pravokoten na ravnino, pobudovanoї na dveh spіv množiteljev, ki je rezultat binarne operacije "vektorsko množenje" nad vektorji v trivialnem evklidskem prostoru. Twіr ni niti komutativen niti asociativen (je antikomutativen) in deluje kot skalarni dobutku vektorіv. Za bogate inženirje in fiziko je nujno, da je mati sposobna biti vektor, ki je pravokoten na obe realnosti – vektorski TV mora biti mogoč. Vektorska razširitev corisny za "obračanje" pravokotnosti vektorjev je dolžina vektorske raztezke dveh vektorjev v smeri raztezanja njunih dožin, saj sta pravokotna, in se spremeni na nič, saj sta vektorja vzporedna oz. antiparalelno.
Vektor tvir je bil dodeljen le trivimerju in prostranstvu sedmih svetov. Rezultat ustvarjanja vektorja, tako kot skalarnega, je v evklidski prostorski metriki.
O pogledu na formulo za izračun koordinat vektorskega skalarnega objekta v tridimenzionalnem pravokotnem koordinatnem sistemu, da formula za vektorski objekt leži v orientaciji pravokotnega koordinatnega sistema ali pa "kiralnost"
Kolinearizem vektorjev.
Dva neničelna (ni enaka 0) vektorja se imenujeta kolinearna, ker ležita na vzporednih ali na isti premici. Dovoljeno je, vendar ni priporočljivo kot sinonim - "vzporedni" vektorji. Kolinearni vektorji so lahko enako ravnani ("smeri") ali nasprotno zravnani (v preostalem primeru jih včasih imenujemo "antikolinearni" ali "antiparalelni").
Zmіshane viroblennya vektorіv( a, b, c)- skalarna razširitev vektorja a na vektorska razširitev vektorja b in c:
(a, b, c) = a ⋅ (b × c)
včasih se imenuje trinarna skalarna tvorba vektorjev, morda prek tistih, katerih rezultat je skalar (natančneje, psevdoskalar).
Geometrični zmist: Modul kreative zmіsha je številčno pomembnejši od obveznosti paralelepipeda, ki ga naredijo vektorji (a, b, c) .
moč
Zmіshané tvir je poševno simetričen glede na vse svoje argumente: t.j. e. permutacija ali obstajata dve spіvmulnikiv spremeni znak ustvarjanja. Rezultati kažejo, da je sprememba poleg desnega kartezijanskega koordinatnega sistema (v ortonormalni bazi) bližja vektorju matrike, zloženemu iz vektorja i:
Spremembe poleg levega kartezijanskega koordinatnega sistema (v ortonormalni osnovi) so enake oznaki matrike, zložene iz vektorjev in vzete z znakom "minus":
Zokrema,
Kot da bi obstajala dva vektorja in vzporedna, potem bo s tretjim vektorjem smrad ustvaril zmedo, ki je enaka nič.
Obstajajo trije vektorji, ki so linearno nepovezani (to je, da so komplanarni, ležijo na isti ravnini), njihova odstopanja pa so enaka nič.
Geometrijski zmist - Zmіshane tvіr za absolutno vrednost obveznega paralepipeda (div. babies), ki ga naredijo vektorji i; znak za polaganje depozita v redu, chi є tsya triyka vektor_v desno chi leva.
Komplanarnost vektorjev.
Trije vektorji (ali več) se imenujejo komplanarni, kot da smrad, zmanjšan na storže, leži v isti ravnini
Prevlada komplanarnosti
Če želite, da je eden od treh vektorjev nič, so trije vektorji lahko tudi koplanarni.
Trio vektorjev za maščevanje paru kolinearnih vektorjev, ki so koplanarni.
Zmishane tvir koplanarni vektorji. Ce je merilo za komplanarnost treh vektorjev.
Vektorji spremljevalci - linearne leže. Tse je tudi merilo za komplanarnost.
V prostoru treh svetov 3 nekomplanarni vektorji vzpostavijo osnovo
Linearno neodvisni in linearno neodvisni vektorji.
Linearni in neodvisni vektorski sistemi.Imenovanje. Vektorski sistem se imenuje linearna ledinače je le ena netrivialna linearna kombinacija teh vektorjev, ki je enaka ničelnemu vektorju. Kakorkoli že, potem. samo trivialna linearna kombinacija teh vektorjev v nič vektorja, se vektorji imenujejo linearno neodvisna.
Izrek (linearno merilo za odpadke). Da bi bil sistem vektorjev v linearnem prostoru linearno nepovezan, je potrebno in zadostno sprejeti enega od teh vektorjev v linearni kombinaciji drugih.
1) Če je srednji vektor, če hočete en ničelni vektor, potem je celoten sistem vektorjev linearno puščen.
Res je, kot na primer vvahayuchi, morda netrivialna linearna kombinacija.
2) Takoj, ko so srednji vektorji vzpostavljeni linearno ležeči sistem, potem je celoten sistem linearno uparjen.
Prav, naj bodo vektorji, linearni depoziti. Prav tako je netrivialna linearna kombinacija, ki je podobna ničelnemu vektorju. Ale todi, ugibam ![]() vzamemo tudi netrivialno linearno kombinacijo, ki je enaka ničelnemu vektorju.
vzamemo tudi netrivialno linearno kombinacijo, ki je enaka ničelnemu vektorju.
2. Osnova in rozmirnist. Imenovanje. Sistem linearno neodvisnih vektorjev ![]() vektorski prostor se imenuje osnova v prostoru, kot da bi vektor lahko predstavil z linearno kombinacijo vektorjev v sistemu, tj. za kožni vektor
vektorski prostor se imenuje osnova v prostoru, kot da bi vektor lahko predstavil z linearno kombinacijo vektorjev v sistemu, tj. za kožni vektor ![]() torej, kaj je lahko mesto ljubosumja Tsya ljubosumje se imenuje vektorska postavitev za osnovo in številke
torej, kaj je lahko mesto ljubosumja Tsya ljubosumje se imenuje vektorska postavitev za osnovo in številke ![]() poklical koordinate vektorja glede na osnovo(sicer pri bazi) .
poklical koordinate vektorja glede na osnovo(sicer pri bazi) .
Izrek (o enotnosti razporeditve za osnovo). Kožo vektorja je mogoče razširiti preko osnove. en čin, tobto. koordinate kožnega vektorja na osnovi jasno izstopajo.
1. naloga. Z'yasuvati, chi sistem vektorjev je linearno neodvisen. Sistem vektorjev je podan z matriko sistema, katere stolpce seštejemo iz koordinat vektorjev.
 .
.
Rešitev. Pridi kombinacija  enaka nič. Ko smo v koordinatah zabeležili enakost qiu, vzamemo naslednji sistem enakosti:
enaka nič. Ko smo v koordinatah zabeležili enakost qiu, vzamemo naslednji sistem enakosti:
 .
.
Takšen sistem enakih se imenuje trikut. Obstaja samo ena rešitev  . Oče, vektorji
. Oče, vektorji  linearno neodvisna.
linearno neodvisna.
2. naloga. Z'yasuvati, chi є linearno neodvisen sistem vektorjev.
 .
.
Rešitev. Vektorji  linearno neodvisna (razdel. problem 1). Recimo, da je vektor linearna kombinacija vektorjev
linearno neodvisna (razdel. problem 1). Recimo, da je vektor linearna kombinacija vektorjev  . Koeficienti postavitve za vektorje
. Koeficienti postavitve za vektorje  umaknjen iz izravnalnega sistema
umaknjen iz izravnalnega sistema
 .
.
Sistem Tsya je kot zapleten, obstaja samo ena rešitev.
Oče, sistem vektorjev  linearno leha.
linearno leha.
Spoštovanje. Matrike te vrste, tako kot v problemu 1, se imenujejo zapleteno , in naloge 2 - pogosto zapleteno . Prehrana linearne ledine vektorskega sistema se zlahka zmoti, kot matrika, zložena iz koordinat teh vektorjev, je pogosto trikotna. Če matrica nima posebnega videza, potem za pomoč elementarna transformacija vrstic , Scho zberіgayut linearno spіvvіdnoshennia mіzh stovptsami, її je mogoče zmanjšati na podobno zapleten videz.
Elementarne transformacije vrstic matrike (EPS) se imenujejo naslednje operacije na matriki:
1) permutacija vrstic;
2) množenje vrstice na dano ničelno število;
3) dodajanje v vrstico naslednje vrstice, pomnoženo z določeno številko.
3. naloga. Poiščite največji linearno neodvisen podsistem in izračunajte rang vektorskega sistema
 .
.
Rešitev. Usmerimo matriko sistema po pomoči NPS na podoben pogosto zapleten videz. Za pojasnitev vrstnega reda dіyja je vrstica s številko matrike, ki se preoblikuje, pomenljiva s simbolom . Na zadnji strani stolpca so puščice prikazane nad vrsticami matrike, saj je potrebno vikonirati, da odstranimo vrstice nove matrike.

 .
.
Očitno je, da sta prva dva stolpca izpuščene matrike linearno neodvisna, tretji stolpec je enaka linearna kombinacija, četrtega stolpca pa ni mogoče najti v prvih dveh. Vektorji  se imenujejo osnovni. Vzpostavljajo maksimalno linearno neodvisen podsistem sistema
se imenujejo osnovni. Vzpostavljajo maksimalno linearno neodvisen podsistem sistema  , In rang sistema je tri.
, In rang sistema je tri.
Osnova, koordinate
4. naloga. Poiščite osnovo in koordinate vektorjev, na kateri osnovi na neosebnih geometrijskih vektorjih, katerih koordinate ugajajo umu  .
.
Rešitev. Bagato je ravno, scho za prehod skozi storž koordinat. Dodatna osnova na ravnini se oblikuje iz dveh nekolinearnih vektorjev. Koordinate vektorjev v izbrani osnovi so določene s sistemom linearnih poravnav rozvyazkoy vydpovidnoy.
Іsnuє th іnshіy sposіb vyvіshennya tsgogo zavdannya, če lahko poznate osnovo za koordinate.
Koordinate  odprt prostor s koordinatami na stanovanju
odprt prostor s koordinatami na stanovanju  ki ni neodvisen. Neodvisne spremenljivke i (ime se imenujejo proste) enolično dodelijo vektor na območju i, zato jih je mogoče vzeti s koordinatami v . Ista osnova
ki ni neodvisen. Neodvisne spremenljivke i (ime se imenujejo proste) enolično dodelijo vektor na območju i, zato jih je mogoče vzeti s koordinatami v . Ista osnova  je sestavljen iz vektorjev, ki ležijo v različnih nizih prostih sprememb
je sestavljen iz vektorjev, ki ležijo v različnih nizih prostih sprememb  і
і  , potem .
, potem .
5. naloga. Poznati osnovo in koordinate vektorjev za vsako osnovo na bogatih vektorjih v prostoru, za katere so neparne koordinate med seboj enake.
Rešitev. Vibero, tako kot jaz v nalogi za naprej, koordinira v prostoru.
tako jag  , potem se boste spremenili
, potem se boste spremenili  enolično dodeli vektorju i, nato, ê koordinate. Spremenljiva osnova je sestavljena iz vektorjev.
enolično dodeli vektorju i, nato, ê koordinate. Spremenljiva osnova je sestavljena iz vektorjev.
6. naloga. Poišči osnovo in koordinate vektorjev, v katerih osnovi na neosebnih vseh matrikah  , de
, de  - Precej.
- Precej.
Rešitev. Matrika kože h je nedvoumno predstavljena v pogledu:
Tse spіvіdnoshennia є razladannyam vektor z osnovi  s koordinatami
s koordinatami  .
.
7. naloga. Poiščite ekspanzijo in osnovo linearne ovojnice vektorskega sistema
 .
.
Rešitev. Predelajmo matriko s koordinatami vektorja v sistemu s pomočjo EPS v podobno zapleten videz.


 .
.
Stovptsi  preostale matrike so linearno neodvisne, preostale pa matrike
preostale matrike so linearno neodvisne, preostale pa matrike  linearno vrazhayutsya krіz jih. Oče, vektorji
linearno vrazhayutsya krіz jih. Oče, vektorji  vzpostaviti osnovo
vzpostaviti osnovo  , і
, і  .
.
Spoštovanje. Osnova y  izbrani dvoumno. Na primer vektor
izbrani dvoumno. Na primer vektor  vzpostaviti tudi osnovo
vzpostaviti tudi osnovo  .
.
Vektorski sistem se imenuje linearna ledina, yakshcho іsnuyet takі številke, med yakhocha bi rad, da je ena vіdminno vіd nič, scho vykonuєtsya spokojnost. >.
Kako lahko mirnost zmaga le v tem primeru, če je vse, potem se imenuje sistem vektorjev linearno neodvisna.
Izrek. Vektorski sistem bo linearna ledina takrat in samo takrat, če želite enega od njenih vektorjev v linearni kombinaciji drugih.
primer 1. Bogati član ![]() je linearna kombinacija bogatih segmentov. Bogati izrazi postanejo linearno neodvisen sistem, tako kot bogat izraz https: //pandia.ru/text/78/624/images/image012_44.gif" width="129" height="24">.
je linearna kombinacija bogatih segmentov. Bogati izrazi postanejo linearno neodvisen sistem, tako kot bogat izraz https: //pandia.ru/text/78/624/images/image012_44.gif" width="129" height="24">.
zadnjica 2. Matrični sistem, https://pandia.ru/text/78/624/images/image016_37.gif" width="51" .ru/text/78/624/images/image019_27.gif" width="69" height= "21"> /images/image022_26.gif" width="40" linearni prah.
Rešitev.
Shranimo linearno kombinacijo teh vektorjev https://pandia.ru/text/78/624/images/image023_29.gif" 22">.
Glede na enake koordinate enakih vektorjev vzamemo width="289" height="69">
Preostanek
 і
і
Sistem ima lahko eno samo trivialno rešitev, tako da linearna kombinacija teh vektorjev doseže nič več kot enkrat, če vsi koeficienti dosežejo nič. Tom danemu sistemu vektor_v linearno neodvisen.
zadnjica 4. Vektorji so linearno neodvisni. Kakšni bodo sistemi vektorjev
a).![]() ;
;
b).![]() ?
?
Rešitev.
a). Dodamo linearno kombinacijo in jo izenačimo z nič
Z uporabo moči operacij z vektorji v linearnem prostoru bomo prepisali preostalo enakovrednost vizualnega
Ker so vektorji linearno neodvisni, morajo biti koeficienti krivde enaki nič, torej gif.
Otrimanov sistem je enak, obstaja le ena trivialna rešitev ![]() .
.
Oskіlki rivnіst (*) vykonuєtsya samo pri - linearno neodvisno;
b). Shranjevanje enakosti https://pandia.ru/text/78/624/images/image039_17.gif" (**)
Zastosovuyuchi analogno mirkuvannya, otrimaєmo
Virishyuchi sistem izravnave po Gausovi metodi, je potreben
 oz
oz
Preostali del sistema je brezosebna rešitev https://pandia.ru/text/78/624/images/image044_14.gif" width="149" height="24 src=">. ljubosumje zmaga (**)
. Oče, sistem vektorjev ![]() - Linearna ledina.
- Linearna ledina.
zadnjica 5 Vektorski sistem je linearno neodvisen, vektorski sistem pa linearno neodvisen. gif. (***)
Pri ljubosumju (***) . Dejansko je bil sistem linearno zapuščen.
Zі spіvіdnoshennia (***)
sprejemljivo ![]() oz
oz ![]() Pomembno
Pomembno ![]() .
.
Odnesi ![]()
Naloga za samostojna rešitev(v občinstvu)
1. Sistem, ki maščuje ničelni vektor, je linearno zapuščen.
2. Sistem, ki je sestavljen iz enega vektorja a, linearno ležerno celo in manj potem, če, a=0.
3. Sistem, ki ga sestavljata dva vektorja, je linearno sodi in le, če sta vektorja sorazmerna (torej eden od njih nastane iz najmanjšega množenja s številom).
4. Če linearnemu izgubljenemu sistemu dodate vektor, boste videli sistem linearnega prahu.
5. Kot iz linearno neodvisnega sistema je vektor viden, sistem vektorjev je linearno neodvisen.
6. Yakscho sistem S linearno neodvisen, vendar postane linearno neodvisen pri dodajanju vektorja b, nato vektor b linearno upogiba skozi vektorje sistema S.
c). Sistem matrik ima drugačen vrstni red matrik.
10. Naj bo sistem vektorjev a,b,c vektorski prostor je linearno neodvisen. Da bi dosegli linearno neodvisnost ofenzivnih vektorskih sistemov:
a).a+b, b, c.
b).a+https://pandia.ru/text/78/624/images/image062_13.gif" width="15" height="19">– dovolj število
c).a+b, a+c, b+c.
11. daj no a,b,c- trije vektorji na ploskvi, med njimi lahko zložite tricutnik. Ali bodo vektorji Chi qi linearno neodvisni?
12. Podano sta dva vektorja a1=(1, 2, 3, 4),a2=(0, 0, 0, 1). Izberite še dva chotirivimirjeva vektorja a3 ina4 torej sistem shob a1,a2,a3,a4 bula linearno neodvisna .
Imenovanje. Linearna kombinacija vektorjev a 1, ..., a n
x 1 a 1 + ... + x n a n.
nepomembno torej so vsi koeficienti x 1 , ..., x n enaki nič.
Imenovanje. Imenuje se linearna kombinacija x 1 a 1 + ... + x n a n netrivialno, tudi če eden od koeficientov x 1, ..., x n ni enak nič.
linearno neodvisna, tako da ni netrivialne kombinacije teh vektorjev, ki bi bila enaka nič vektorju .
Torej so vektorji a 1 ..., a n linearno neodvisni, kot je x 1 a 1 + ... + x n a n = 0 sodo in le, če je x 1 = 0, ..., x n = 0.
Imenovanje. Vektorji a 1 , ..., a n se imenujejo linearna ledina yakscho іsnuє netrivialna kombinacija tsikh vector_v do_vnyuє nič vektorja.
Dominantnost linearnih vektorjev:
Za n-te vektorje.
n + 1 vektor linearnih depozitov.
Za 2 in 3 svetovne vektorje.
Dve vrstici ležeči vektor- kolinearno. (Vektorji Kolіnearnі - linearni depoziti.) .
Za tri miroljubne vektorje.
Trije linearni ležeči vektorji - komplanarni. (Tri koplanarni vektorji - linearni depoziti.)
Uporabite nalogo za linearno neodvisnost in linearno neodvisnost vektorjev:
Primer 1. Preobrat vektorja a = (3; 4; 5), b = (-3; 0; 5), c = (4; 4; 4), d = (3; 4; 0) so linearno neodvisni.
rešitev:
Vektorji bodo linearno neodvisni, vektorji skaliranja bodo manjši za število vektorjev.
Primer 2. Preobrat vektorja a = (1; 1; 1), b = (1; 2; 0), c = (0; -1; 1) so linearno neodvisni.
rešitev:
| x1 + x2 = 0 | |
| x1 + 2x2 - x3 = 0 | |
| x1 + x3 = 0 |
| 1 | 1 | 0 | 0 | ~ | ||
| 1 | 2 | -1 | 0 | |||
| 1 | 0 | 1 | 0 |
| ~ | 1 | 1 | 0 | 0 | ~ | 1 | 1 | 0 | 0 | ~ | ||||
| 1 - 1 | 2 - 1 | -1 - 0 | 0 - 0 | 0 | 1 | -1 | 0 | |||||||
| 1 - 1 | 0 - 1 | 1 - 0 | 0 - 0 | 0 | -1 | 1 | 0 |
iz prve vrste se vidi drugo; do tretje vrste dodamo drugo:
| ~ | 1 - 0 | 1 - 1 | 0 - (-1) | 0 - 0 | ~ | 1 | 0 | 1 | 0 | ||||
| 0 | 1 | -1 | 0 | 0 | 1 | -1 | 0 | ||||||
| 0 + 0 | -1 + 1 | 1 + (-1) | 0 + 0 | 0 | 0 | 0 | 0 |
Ta rešitev kaže, da lahko sistem naredi brezosebno rešitev, tako da ima kombinacijo vrednosti številk x 1 x 2 x 3, ki ni nič, tako da je linearna kombinacija vektorjev a, b, c enaka ničelni vektor, na primer:
A + b + c = 0
a tse pomeni, da so vektorji a, b, c linearni depoziti.
predlog: vektorji a, b, c so linearno neodvisni.
Primer 3. Preobrat vektorja a = (1; 1; 1), b = (1; 2; 0), c = (0; -1; 2) so linearno neodvisni.
rešitev: Poznamo vrednosti koeficientov za katero koli linearno kombinacijo teh vektorjev v ničelnem vektorju.
x 1 a + x 2 b + x 3 c 1 = 0Tse vektorsko poravnavo lahko zabeležimo v vizualnem sistemu linearnih poravnav
| x1 + x2 = 0 | |
| x1 + 2x2 - x3 = 0 | |
| x1 + 2x3 = 0 |
Sistem vikorista preverjamo z Gaussovo metodo
| 1 | 1 | 0 | 0 | ~ | ||
| 1 | 2 | -1 | 0 | |||
| 1 | 0 | 2 | 0 |
iz druge vrste se vidi prva; iz tretje vrstice vidimo prvo:
| ~ | 1 | 1 | 0 | 0 | ~ | 1 | 1 | 0 | 0 | ~ | ||||
| 1 - 1 | 2 - 1 | -1 - 0 | 0 - 0 | 0 | 1 | -1 | 0 | |||||||
| 1 - 1 | 0 - 1 | 2 - 0 | 0 - 0 | 0 | -1 | 2 | 0 |
iz prve vrste se vidi drugo; do tretje vrste dodamo drugo.
Linearna ledina linearna neodvisnost vektor_v.
Vektorske baze. Atenski koordinatni sistem
V avditoriju je veliko čokolad, nekaj sladkega korena pa bo danes lahko pobegnilo od kože - analitična geometrija z linearno algebro. Ta članek bo razdeljen na dva dela napredna matematika, mi pa se čudimo, kako se smradi navadijo na en hrib. Vzemite si odmor, s'zh "Tviks"! ... baby, no, super punčka. Če hočem, ne bom zadel, oprosti, lahko imam pozitivno razpoloženje za trening.
Linearna lega vektorjev, linearna neodvisnost vektorjev, vektorska osnova ta izraz morda ni le geometrijska interpretacija, ampak najprej algebraični smisel. Sam koncept "vektorja" z vidika linearne algebre še zdaleč ni enak "superiornemu" vektorju, ki ga lahko predstavljamo na ravnini prostora. Za dokaz vam ni treba iti daleč, poskusite naslikati vektor petdimenzionalnega prostora. ![]() . Abo samo počakaj, za nekatere sem šel v Gіsmeteo: - temperatura in atmosferski tlak sta dobra. Zadnjica očitno ni pravilna z vidika avtoritete vektorskega prostora, vendar nič ne preprečuje formalizacije podatkov s parametri in vektorjem. Dih jeseni.
. Abo samo počakaj, za nekatere sem šel v Gіsmeteo: - temperatura in atmosferski tlak sta dobra. Zadnjica očitno ni pravilna z vidika avtoritete vektorskega prostora, vendar nič ne preprečuje formalizacije podatkov s parametri in vektorjem. Dih jeseni.
Živjo, ne bom vas poskušal zamikati s teorijo, linearnimi vektorskimi prostori, težava je v tem, razumeti definicijo tega izreka. Novi izrazi (linearni depozit, neodvisnost, linearna kombinacija, osnova itd.) so z vidika algebre pridevniki vsem vektorjem, vendar bo aplikacija podana geometrijsko. V tem rangu je vse preprosto, dostopno na prvi pogled. Krіm zavdan analitična geometrija velja za tipično nalogo algebre. Za obvladovanje snovi se je treba naučiti lekcije Vektorji za čajnikeі Kako šteti?
Linearna ledina in neodvisnost vektorja v ravnini.
Območna osnova in afinitetni koordinatni sistem
Poglejmo vaše območje računalniška miza(samo miza, nočne omarice, posteljna polena, stele, kdor rabi). Vodja področja v prihodnjih dneh:
1) Izberite osnovo območja. Približno kazhuchi, stіlnitsa maє dovzhina і širina, je bilo intuitivno spoznano, da sta potrebna dva vektorja za stimulacijo osnove. En vektor očitno ni dovolj, trije vektorji so zayva.
2) Na podlagi obrnjene osnove nastavite koordinatni sistem(koordinatna mreža), da dodelite koordinate vsem predmetom, ki so na mizi.
Ne bodite presenečeni, razlaga bo na prstih. In na tvojem. Bodi prijazen, odpusti izrazen prst leve roke do roba sloga, tako da sem se čudil monitorju. Tse bo vektor. Zdaj pa mesto mezinec desne roke na robu mize kar tako - schob buv ravnanje na zaslonu monitorja. Tse bo vektor. Nasmehni se, izgledaš čudovito! Kaj lahko rečete o vektorjih? Podatkovni vektorji kolinearno, kar pomeni linearno obrni enega skozi enega:
, no, chi navpaki: , de - deake številka, vіdmіnne vіd nič.
Sliko, katere dejanje si lahko ogledate v lekciji Vektorji za čajnike De sem razložil pravilo množenja vektorja s številom.
Chi bodo vaši prsti postavili osnovo na računalniško mizo? Očitno ne. Kolіnearnі vektorji in dvig cen tu in tam sam naravnost, območje pa je lahko daljše in širše.
Takšni vektorji se imenujejo linearna ledina.
zaključek: Besede "linearno", "linearno" pomenijo tiste stvari, ki imajo matematično enake, ni kvadratov, kock, drugih korakov, logaritmov, sinusov. Є tіlki linіynі (1. stopnja) proti ledini.
Dve vektorski ravnini linearne depozite takrat in samo takrat, če je smrad kolinearen.
Prekrižite prste na mizi, tako da boste med njimi kot rez Krima 0 ali 180 stopinj. Dve vektorski ravninilinearno ne zastarel v tem in manj, ker smrad ni kolinearen. Otzhe, osnova je odvzeta. Ni vam treba skrbeti, da je osnova pogledov »pokošena« z nepravokotnimi vektorji različnih dolžin. Zame ni nenavadno, da pri jogi dodatek ni samo 90 stopinj in ne samo en sam, enak staremu vektorju.
Be-yaky ploščati vektor en čin razširjeno glede na osnovo: ![]() , de - dіysnі številke. Klicne številke vektorske koordinate na kateri podlagi.
, de - dіysnі številke. Klicne številke vektorske koordinate na kateri podlagi.
Tako se zdi vektornastopi na ogled linearna kombinacija baznih vektorjev. Tobto viraz se imenuje vektorska postavitevosnova oz linearna kombinacija bazni vektorji.
Na primer, lahko rečemo, da je vektor postavitve za ortonormalno osnovo ravnine, ali pa lahko rečemo, da so predstavitve linearne kombinacije vektorjev napačne.
Formulirajte dodelitev na osnovo formalno: Osnova območja par linearno neodvisnih (nekolinearnih) vektorjev se imenuje, , pri katerem Bodi kot Ravninski vektor je linearna kombinacija osnovnih vektorjev.
Sam trenutek imenovanja je dejstvo, da so vektorji prevzeti po vrstnem redu pesmi. Basisi ![]() - obstajata dve popolnoma različni bazi! Kot se zdi, mezinca leve roke ni mogoče premakniti na mezinec desne roke.
- obstajata dve popolnoma različni bazi! Kot se zdi, mezinca leve roke ni mogoče premakniti na mezinec desne roke.
Osnovo smo izdelali, vendar še vedno ni dovolj, da nastavite koordinatno mrežo in dodelite koordinate skin objektu vaše računalniške tabele. Zakaj ste zamudili? Vektorji so vilni in se zameglijo po celotni ravnini. Kako torej dodeliti koordinate tem majhnim potepuškim točkam na mizi, ki so ostale po burnem vikendu? Zahtevana smernica. І tak mejnik je vsem znana točka - storž koordinat. Izbere se iz koordinatnega sistema:
Začel bom s "šolskimi" organizacijami. Že pri uvodni lekciji Vektorji za čajnike Videl sem dejanja prepoznavanja med pravokotnim koordinatnim sistemom in ortonormalno osnovo. Standardna slika osi:

Ko govorimo o pravokotni koordinatni sistem, potem se najpogosteje uporablja kos koordinat, koordinatna os in merilo vzdolž osi. Poskusite v iskalni sistem vnesti "pravokotni koordinatni sistem" in povedali boste, da vam je vredno povedati o znanju 5-6. razreda koordinatne osi in o tem, kako postaviti točke na ravnino.
Po drugi strani pa obstaja učinek, da je pravokotni koordinatni sistem mogoče določiti kot celoto z ortonormalno osnovo. І tse mayzhe so. Formula zveni takole:
storž koordinat, і ortonormalizacija postaviti osnovo Kartezijev pravokotni koordinatni sistem ravnine . To je pravokoten koordinatni sistem vsekakor so predstavljeni z eno točko in dvema enojnima ortogonalnima vektorjema. Ravno zaradi tega potrebujete stol, saj sem vsadil vishche - noter geometrijske težave pogosto (čeprav ne zavzhd) barve і vektorje, і koordinatne osi.
Mislim, da so vsi razumeli, da je za dodatno točko (stop koordinat), ki je ortonormalna na osnovo BE-YAKIY TOČKE območja in BE-YAKIYA VEKTOR območja lahko dodelite koordinate. Figurativno, očitno, "na kvadratu je mogoče vse oštevilčiti."
Ali so koordinatni vektorji lahko enojni? Nі, smrad lahko mati dovіlnu ne-nič dovzhina. Poglejmo točko in dva ortogonalna vektorja ter dokaj neničelne vrednosti:

Takšna osnova se imenuje ortogonalno. Koordinatni storž z vektorji nastavi koordinatno mrežo in naj bo to točka ravnine, pa naj bo to vektor, ki zapiše svoje koordinate v to osnovo. Na primer oz. Očitna nesposobnost je v tem, da so koordinatni vektorji na vrhu hribažalujejo za različnimi življenji, vіdminnі vіd odinitsі. Takoj ko je osamljenost enaka, potem pride ven primarna ortonormalna osnova.
! Opomba : v ortogonalni osnovi in tudi nižje v atenskih osnovah se upoštevajo ravnine in prostor ene vzdolž osi UMOVIMI. Na primer, v eni enoti vzdolž osi abscise je 4 cm, v eni enoti vzdolž ordinatne osi 2 cm.
In druga hrana, na jaku, je res dokaz - kakšen obov'yazykovo kut med osnovnimi vektorji lahko doseže 90 stopinj? Živjo! Kako potrditi sestanek, osnovni vektorji in pristojbine manj kot nekolinearno. Vіdpovidno kut mozhe buti be-yakim, krіm 0 in 180 stopinj.
Točka letala, kot se imenuje storž koordinat, і nekolinearno vektorji , , set afini koordinatni sistem ravnine :

Z drugimi besedami, tak koordinatni sistem se imenuje pletena sistem. Kako uporabiti točke in vektorje na sliko fotelja: 
Kot veste, je atenski koordinatni sistem manj enostaven, ne uporabljajo formul za vektorje in vdrіzkiv, kot smo si ogledali drugi del lekcije Vektorji za čajnike, bogato slane formule, pov'yazanі z skalarno ustvarjanje vektorjev. Potem so tu še poštena pravila za zlaganje vektorja in množenje vektorja s številom, formule za razčlenitev na dani izraz in tudi za deaking vrste nalog, ki si jih zlahka ogledamo.
In visnovok je takšen, da je najprimernejši način za klic točke atenskega koordinatnega sistema - kartezijanskega pravokotnega sistema. K temu ji bi najraje, najpogosteje in me pripeljali na bachiti. ... Medtem je v tem življenju vse jasno - malo je situacij, v katerih je reka sama poševna (sicer npr. polarno) koordinatni sistem. Tisti humanoidi lahko uživajo v takšnih sistemih =)
Preidimo na praktični del. Usі zavdannya ta lekcija je tako kot pravokotni koordinatni sistem, tako zagalnogo atenski vpadku. Tukaj ni nič zložljivega, vse gradivo je dostopno šolarju.
Kako določiti kolinearnost vektorja v ravnini?
Tipična reka. Da bi imeli dva vektorja in področja ![]() biti kolinearni, potrebni in zadostni, tako da so njihove ustrezne koordinate sorazmerne. Pravzaprav je to koordinatna podrobnost očitnega spivvіdnoshenya.
biti kolinearni, potrebni in zadostni, tako da so njihove ustrezne koordinate sorazmerne. Pravzaprav je to koordinatna podrobnost očitnega spivvіdnoshenya.
zadnjica 1
a) Reverzni, chi kolinearni vektorji ![]() .
.
b) Chi vzpostavi osnovo vektorja ![]() ?
?
rešitev:
a) Zakaj, kaj velja za vektorje ![]() koeficient sorazmernosti, tako da so zmagale enakosti:
koeficient sorazmernosti, tako da so zmagale enakosti: ![]()
Obov'yazkovo rozpovіm o "pіzhonskiy" različici pravil zastosuvannya tsgogo, ki kroži v praksi. Ideja je v tem, da boste takoj sešteli delež in se vprašali, ali boste imeli prav:
Dodajmo delež danih koordinat vektorjev:
kmalu:
, v tem vrstnem redu so ustrezne koordinate sorazmerne,
Nastavitev je mogoče zložiti in zložiti, dragocena možnost:
Za samopreverjanje lahko zakukate tiste, ki so kolinearni vektorji, in linearno upognete enega skozi enega. S tega vidika obstaja mesto enakovrednosti ![]() . Vaša poštenost se zlahka perveryaetsya z osnovnimi delitvami z vektorji:
. Vaša poštenost se zlahka perveryaetsya z osnovnimi delitvami z vektorji: 
b) Dva vektorja in ravnine vzpostavita osnovo, kot da bi bila kolinearna (linearno neodvisna). Doslіdzhuєmo na kolіnearnіst vektorji ![]() . Zgradimo sistem:
. Zgradimo sistem: 
Od prvega enakega kričiš, scho, od drugega enakega, kričiš, oh, sistem je nor(Ni rešitve). Na ta način ustrezne koordinate vektorjev niso sorazmerne.
Visnovok: vektorji so linearno neodvisni in tvorijo osnovo.
Poenostavljena različica rešitve izgleda takole:
Dodamo delež danih koordinat vektorjev ![]() :
:
, Otzhe, vektorji qi in linearno neodvisni in vzpostavijo osnovo.
Pokličite to možnost, da zavrnete pregledovalce, vendar za napake krivite težavo, če so koordinate enake nič. os takole: ![]() . Abo takole:
. Abo takole: ![]() . Abo takole:
. Abo takole: ![]() . Kako lahko delam tukaj prek sorazmerja? (Resnično, ne morete deliti z nič). Iz istega razloga sem enostavnejšo rešitev poimenoval "pizhonsky".
. Kako lahko delam tukaj prek sorazmerja? (Resnično, ne morete deliti z nič). Iz istega razloga sem enostavnejšo rešitev poimenoval "pizhonsky".
predlog: a), b) odobriti.
Majhen ustvarjalni primer za samostojno vizijo:
zadnjica 2
Za katero koli vrednost vektorskega parametra ![]() bo kolinearna?
bo kolinearna?
Za rešitev se parameter najde prek razmerja.
Uporabljamo metodo algebre ponovnega preverjanja vektorjev za kolinearnost.
Za dva vektorja v območju enakovredne trdote:
2) vektorji in vzpostaviti osnovo;
3) vektorji niso kolinearni;
+ 5) oscilator, zloži iz koordinat teh vektorjev, vіdminny vіd nič.
Vidpovidno, enakovredna protratilna trdota stopala:
1) vektorski in linearni depoziti;
2) vektorji ne izpolnjujejo osnove;
3) vektorji in kolinearji;
4) vektorje je mogoče linearno obrniti enega skozi enega;
+ 5) vektor, ki se zloži iz koordinat teh vektorjev, kar vodi do nič.
V to sem že prepričan danem trenutku vse izraze, ki ste se jih naučili, ste že razumeli in potrdili.
Oglejmo si novo poročilo, peti odstavek: dva vektorja in ravnine ![]() kolіnearnі thodі і tіlki tіlki todі, če se vyznachnik, zloži iz koordinat teh vector_v, do_vnyuє nič:. Za zastosuvannya tsієї znake, seveda, je treba spomniti poznajo vizionarje.
kolіnearnі thodі і tіlki tіlki todі, če se vyznachnik, zloži iz koordinat teh vector_v, do_vnyuє nič:. Za zastosuvannya tsієї znake, seveda, je treba spomniti poznajo vizionarje.
Virishima Primer 1 na drugačen način:
a) Izračun števila vektorjev, seštevanje koordinat vektorjev ![]() :
:![]() , tudi q vektorji in kolinearji.
, tudi q vektorji in kolinearji.
b) Dva vektorja in ravnine vzpostavita osnovo, kot da bi bila kolinearna (linearno neodvisna). Izračunavanje števila vektorjev, zlaganje koordinat vektorjev ![]() :
:![]() , Otzhe, vektorji so linearno neodvisni in vzpostavljajo osnovo.
, Otzhe, vektorji so linearno neodvisni in vzpostavljajo osnovo.
predlog: a), b) odobriti.
Izgleda bistveno bolj kompaktno in lepše, nižja rešitev z razmerji.
S pomočjo preučenega materiala je mogoče ugotoviti kolinearnost vektorjev, pa tudi vzporednost vdrіzkіv, ravnih črt. Oglejmo si nekaj nalog iz določenih geometrijskih oblik.
zadnjica 3
Glede na vrhove čotirikutnika. Prinesi, da je čotirikutnik paralelogram.
Prinašanje: Fotelj v nalogi ne bo potreben, drobci rešitve bodo zgolj analitični
paralelogram
imenuje se čotirikutnik, ki ima nasprotne strani v parih vzporedno.
V tem vrstnem redu je potrebno prinesti:
1) vzporednost nasprotnih strani;
2) vzporednost nasprotnih strani.
prinašamo:
1) Vektorje poznamo: 
![]()
2) Vektorje poznamo: 
Viyshov je isti vektor ("po šoli" - enaki vektorji). Kolіnearnіst je že očiten, a rešitev je bolje urediti pravilno, z razporeditvijo. Izračunajmo število vektorjev in zložimo koordinate vektorjev: ![]() , Otzhe, qі vektorji in kolinearnі, i.
, Otzhe, qі vektorji in kolinearnі, i.
Visnovok: Protilezhnі strani chotirikutnik v parih vzporedno, otzhe, vіn є paralelogram za sestanke. Kaj je bilo potrebno prinesti.
Več številk dobrih:
zadnjica 4
Glede na vrhove čotirikutnika. Prinesti, scho chotirikutnik є trapezієyu.
Za suvoristično formulo, dokažite jo lepše, sijajno, narišite oznako trapeza in jo samo dopolnite in samo ugibajte, kot da gledate ven.
Tse zavdannya neodvisna rešitev. Zunanja rešitev kot lekcija.
In zdaj je napočil čas, da se iz stanovanja počasi premaknemo na prosto:
Kako označiti kolinearnost vektorja v prostoru?
Pravilo je podobno. Da sta dva vektorja v prostor kolinearna, je potrebno in zadostno, da so njune koordinate sorazmerne.
zadnjica 5
Z'yasuvati, chi kolіnearnі bo napredoval vektorje in prostor:
a);
b)
v) ![]()
rešitev:
a) Reverzibilno je chi koeficient sorazmernosti za različne koordinate vektorjev:
Sistema ni mogoče razrešiti, zato vektorji niso kolinearni.
"Sproschenka" je sestavljena s ponovnim razmerjem. V tem pogledu:
– relativne koordinate niso sorazmerne, zato vektorji niso kolinearni.
predlog: vektorji niso kolinearni.
b-c) To so točke samostojne odločitve. Poskusite jogo okrasiti na dva načina.
Uporabite metodo ponovnega preverjanja vektorjev prostora za kolinearnost preko spremenljivke tretjega reda, ta metoda je prikazana v članku Vektor TV vektor.
Podobno kot pri ravnem pogledu vida orodja ga je mogoče popraviti z metodo ohranjanja vzporednosti odprtih prostorov in ravnih črt.
Vljudno vas prosimo v drugo divizijo:
Linearna zastarelost in neodvisnost sta vektorja v trivimernem prostoru.
Prostorna osnova in afinitetni koordinatni sistem
Veliko zakonov, kot smo videli na trgu, bo poštenih in prostornih. Poskušal sem čim bolj zmanjšati povzetek teorije, kosi levega dela informacij so že razvozlani. Tim ni nič manj, priporočam, da si spoštljivo preberete uvodni del, drobci so novi pojmi in razumete.
Zdaj je zamenjava območja računalniške mize razširjena na tridimenzionalni prostor. Ustvarimo osnovo za jogo. Kdo ve naenkrat v hiši, kdo je na ulicah, v vsakem primeru pa ne moremo nikamor v treh svetovih: širini, dolžini in višini. Zato so za induciranje osnove potrebni trije vektorji prostora. En ali dva vektorja nista dovolj, četrtine so zayvi.
Spet sem rozminaєmos na prstih. Bodite prijazni, dvignite roko navzgor in dvignite mozolj na različnih straneh super, impresivno sredinec . Tse bodo vektorji, smrad se bo čudil na različnih straneh, žaloval za različnimi dožinami in med seboj žaloval za različnimi kuti. Vіtayu, osnova trivimirskega prostranstva je pripravljena! Pred govorom ni treba demonstrirati takšnih vikladov, na primer ne zvijajte prstov, vendar ne morete nikamor =)
Dajmo pomemben obrok, biti kot trije vektorji in zadovoljevati osnovo trivi-svetovnega prostora? Bodite prijazni, trdno stisnite tri prste ob računalniško mizo. Kaj se je zgodilo? Trije vektorji so romali v isti ravnini in približno se zdi, da imamo en znak vimiriva - višino. Takšni vektorji komplanarno In povsem očitno je, da podlage za trivimerni prostor ni mogoče ustvariti.
Treba je opozoriti, da koplanarni vektorji in nič narobe ležijo na isti ravnini, lahko so na vzporednih ravninah (poskusite delati le s prsti, da bi Salvador Dali manj navijal =)).
Imenovanje: vektorji so poimenovani komplanarno kot pravi stan, kot vzporedni smrad. Tukaj je logično dodati, da če takšnega območja ni, potem vektorji ne bodo koplanarni.
Trije koplanarni vektorji in linearni depoziti tobto linearno vrazhayutsya enega skozi enega. Zaradi preprostosti je spet sprejemljivo, da smrad leži v enem stanovanju. Prvič, vektorji in ne samo to, so koplanarni, lahko so bolj kolinearni, tudi če je vektor viden skozi vektor. Na drug način, na primer, vektorji niso kolinearni, potem se tretji vektor obrne skozi njih v enem samem vrstnem redu: ![]() (in zakaj je za materiale prejšnje delitve enostavno uganiti).
(in zakaj je za materiale prejšnje delitve enostavno uganiti).
Pošteno je vrnitev trditve: trije nekoplanarni vektorji in linearno neodvisni vektorji, tobto že n_yak ne vrazhayutsya enega skozi enega. Jaz sem očitno manj kot taki vektorji in lahko zadovoljim osnovo trivialnega prostora.
Imenovanje: Osnova trivimirnega prostranstva imenujemo trio linearno neodvisnih (nekomplanarnih) vektorjev, vzeto iz pevskega reda kadarkoli, pa naj bo to vektor odprtega prostora en čin razpršeno po dani bazi , de koordinate vektorja v dani bazi
Če ugibate, lahko rečete tudi, da je vektor reprezentacij linearna kombinacija bazni vektorji.
Koncept koordinatnega sistema je predstavljen na enak način, tako kot za ravno pobočje zadostuje ena točka in trije linearno neodvisni vektorji:
storž koordinat, і nekoplanarno vektorji , vzeto iz pevskega reda, set afinni sistem koordinat trivi-svetovnega prostora
:
Očitno koordinatna mreža »pletenice« ni zelo učinkovita, vendar nam pozivni koordinatni sistem omogoča, da vsekakor označite koordinate katerega koli vektorja, ki so koordinate katere koli točke v prostoru. Podobno kot ravnina tudi v atenskem koordinatnem sistemu prostor ne dela enakih formul, o katerih sem že ugibal.
Najbolj primarni in najbolj priročen izraz za afinitetni koordinatni sistem є pravokotni koordinatni sistem:
Pokažite na prostor, kot se imenuje storž koordinat, і ortonormalizacija postaviti osnovo Kartezijev pravokotni koordinatni sistem
. Poznaj sliko: 
Pred tem, kako preiti na praktične naloge, bom ponovno sistematiziral informacije:
Za tri vektorje v prostoru, ki so enakovredni isti togosti:
1) vektorji so linearno neodvisni;
2) vektorji in vzpostaviti osnovo;
3) vektorji niso komplanarni;
4) vektorjev ni mogoče linearno obrniti enega skozi enega;
5) vyznachnik, zlaganje koordinat teh vektorjev, vіdminny vіd nič.
Protilezhnі vyslovlyuvannya, ugani, zrozumіlі.
Linearni padec/neodvisnost vektorja v prostoru se tradicionalno pregleda s pomočjo imenovanega (5. odstavek). Ti, scho izgubljen praktične naloge nosijo jasen izraz algebraičnega značaja. Čas je, da obesite geometrijski ključ na rože in mahnete z bejzbolsko palico linearne algebre:
Trije vektorski prostori complanarnі thodі і tіlki tіlki tіlі, če je vyznachnik, zložene koordinate danih vektor_v, do_vnyuє nič :  .
.
Pozoren sem na majhen tehnični odtenek: koordinate vektorjev je mogoče zabeležiti ne le v stolpcu, ampak v vrstici (vrednost vektorja se ne spremeni - moč vektorjev je neverjetna). Ale bogatejši je lepši pri stovptsі, oskіlki tse vigіdnіshe za izpolnjevanje nekaterih praktičnih nalog.
Tim bralcem, ki so pozabili metode rozrahunke diplomantov ali pa so v njih slabo orientirani, priporočam eno mojih najstarejših lekcij: Kako šteti?
zadnjica 6
Preverite, ali naslednji vektorji določajo osnovo trivialne širine:
Rešitev: Dejansko se vse odločitve sprejemajo po izračunu dolžnika
a) Izračunajte spremenljivko, prepognite iz koordinat vektorja_v (spremenljivka razširitve vzdolž prve vrstice): 
, Otzhe, vektorji so linearno neodvisni (niso komplanarni) in vzpostavljajo osnovo trivialnega prostora.
Vidpovid: dani vektorji in izpolnjujejo osnovo
b) To je točka neodvisne odločitve. Navzven je rešitev v tem, da je podobna lekciji.
Crawl in ustvarjalni delavci:
zadnjica 7
Za katero vrednost parametra bodo vektorji komplanarni?
Rešitev: Vektorji in komplanarni todі і tіlki tіlki dі, če je vyznachnik, zloži koordinate teh vektorjev na nič: 
Pravzaprav je treba biti enak vyznachniku. Polije se na ničle kot šuliki na jerboe - označevalec navigatorja, da odkrije v drugi vrsti in v vrsti, iskal bom minuse: 
Izvedemo nadaljnjo razširitev in jo obrnemo z desne na najpreprostejšo linearno poravnavo: ![]()
Vidpovid: pri
Tu je enostavno uskladiti, za kar je treba utemeljiti vrednost nekdanjega uradnika in premisliti  , odpiranje joge na novo.
, odpiranje joge na novo.
Na koncu si bomo ogledali še enega tipične naloge, ki je bolj algebraične narave in je tradicionalno vključen v tečaj linearne algebre. Tla so razširjena, kar je zaslužno za velik vrh:
Da bi to 3 vektorje vzpostavili osnovo trivi-svetovnega prostora
in poznamo koordinate 4. vektorja v dani bazi
zadnjica 8
Podan vektor. Pokažite, da vektorji izpolnjujejo osnovo trivimernega prostora in poznajo koordinate vektorja v kateri bazi.
Rešitev: Na zadnji strani glave pobiramo um. Za um so mu dani chotiri vektorji in, tako kot Bachite, je smrad že mayut koordinate v isti osnovi. Kaj je osnova - ne dražite nas. In če rečem kaj takega: trije vektorji kot celota lahko vzpostavijo novo osnovo. Prva stopnja spet temelji na rešitvah Dodatka 6, treba je preveriti, ali so vektorji res linearno neodvisni:
Izračunajmo število vektorjev in zložimo koordinate vektorjev: 
, Otzhe, vektorji so linearno neodvisni in vzpostavljajo osnovo trivi-svetovnega prostora.
! pomembno : vektorske koordinate obov'azkovo posneti na postaji vyznachnika, ne v vrstah. V nasprotnem primeru bo prišlo do goljufije v nadaljnjih algoritmih rozvyazannya.