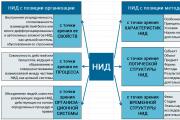
Prejdite sa medzi trikmi vzorca elipsy. Kanonická rovnosť elipsy
Môžete ukázať (veľmi nie plaché), že rovná sa (2) rovná sa rovná (1), aj keď to bolo odobraté z (1) spôsobu neekvivalentné preskupiť. Tse znamená, že ekvivalencia (2) je ekvivalencia danej elipsy. Vono sa volá kanonický(Tobto väčšina odpúšťa).
Došlo mi, že rovnosť elipsy sa rovná inému poriadku, tobto. elіps-line 2. rádu.
Pre elipsy uvádzame porozumenie výstrednosť. Hodnota Tse. Pre elipsy výstrednosť. tak jaka hі a vіdomі, tezh vidomy. Viraz, že ohniskové polomery bodu M(x, y) elipsy sa dajú ľahko získať z predného zrkadlenia: . r 2 známe z rovnosti (3)
Rešpekt Podobne zapichnite dva kvety (F1 a F2) do štýlu, oboma koncami k nim priviažte šnúrku, dozhina, ktorá je väčšia na pestovanie medzi kvetmi ( 2a), potiahnite šnúru a veďte kolísku pozdĺž stola s vrecom, potom otočte uzavreté zakrivené elipsy, pretože sú symetrické k obom osám a klasu súradníc.
4. Sledovanie tvaru elipsy z jogovej kanonickej úrovne.
Pri rešpektovaných mi rkuvanových nepresnostiach bolo urobené visnovo o tvare elipsy. Teraz vykonáme skúmanie tvaru elipsy a analyzujeme kanonické zarovnanie joga:
Poznáme krížové body so súradnicovými osami. Ak y=0, potom , , potom. sú dva body A1(-a,0) a A2(a,0). Ak x = 0, potom . Tobto. môžu byť dva body B1(0,-b) a B2(0,b) (lebo teda). Meno bodov A1, A2, B1, B2 vrcholy elipsy.
2) Oblasť oplachovania elipsy je možné definovať z nasledujúceho mirkuvanu:
a) od rovného elіpsa sld, scho, tobto. , potom. alebo .
b) podobne tobto. alebo . Tse ukazujú, že celé elіpy roztashovanki majú rovný strih, posiate rovným i.
3) Ďalej, v zarovnaní elipsy zmeny x a y, zadávajte iba v dvojitých krokoch, ale to znamená, že krivka je symetrická pozdĺž osí kože a pozdĺž klasu súradníc. D-ale, ak má polomer bod (x, y), potom body i (x, -y), (-x, y) a (-x, -y) by mali ležať. Stačí, aby sa pozrel na tú časť elіps, ako keby ležal v prvej štvrtine, de i.
4) Prvý riadok elipsy je maєmo, ale prvá štvrtina. Ak x = 0, potom y = b. Bod je B2(0,b). Nech sa x zvýši z 0 na a, potom sa y zmení z b na 0. Tim bod M(x, y), počnúc bodom B2(0, b), opisujúcim oblúk do bodu A(a, 0) . Môžete pokojne priniesť, že oblúk vydutia je priamo do hory. Zrkadlením oblúka v súradnicových osiach i na klase vezmeme celé elipsy. Osi symetrie elipsy sa nazývajú osi jogo, bod Properitín je ix-stred elipsy. Dovzhina vіdrіzkіv OA1=ОА2=a sa nazýva veľký pіvvіssya elіps, vіdrіzkіv OV1, OB2=b-malý pіvvіssyu elіps, (a>b), c-jedno ohnisko. Vysvetlite hodnotu geometricky.
Keď a \u003d b, vezmeme kanonické zarovnanie elipsy - zarovnanie kolíka. Pre podiel, tobto. F1 = F2 = 0. .
V tomto poradí krúžok okremy vipadok elіps, ak ohniská jogy prebiehajú okolo stredu a excentricita = 0. Čím väčšia je excentricita, tým väčší je ťah elipsov.
Rešpekt. Z kanonického zarovnania elipsy je ľahké vytvárať visnovoky, takže elipsu je možné nastaviť v parametrickej forme. x = cena t
y=b sin t, de a, b - veľké a malé pіvosі, t-kut.
5. Označenie tej vízie kanonického vyrovnania hyperboly.
Hyperbola sa nazýva GMT oblasti, pre určitý rozdiel medzi dvoma pevnými bodmi F1F2 oblasti, nazývanými ohniská, є konštantná hodnota (nerovná sa 0 a menej, nižšia ohnisková vzdialenosť F1F2).
Povedzme, ako predtým, F1F2=2с a rozdiel je 2а (а<с). Систему координат выберем как и в случае эллипса.
Nech M (x, y) - bod toku hyperboly. Po dohode MF1-MF2= alebo r1-r2== alebo -(1). -tse i є vyrovnanie hyperboly.
Ak vezmeme do úvahy iracionalitu v (1): povedzme jednu odmocninu, odmocnime druhú mocninu, odoberme ju: inak ju odmocnime znova:
Zvіdki.
Rozdeľme to na . Zavedieme notáciu. Todi - (2). Rivnyannya (2), ako sa dá ukázať, je viac rovné ako rovné (1), a to sa rovná hyperbole. Yogo meno kanonické rovná sa hyperbole Bachimo, čo sa tiež rovná hyperbole inej úrovne, hyperbolická čiara iného rádu.
Výstrednosť hyperboly. Viraz ohniskové polomery cez ľahko otrimati spredu, potom poznáme z.
6. Následná forma hyperboly pre її kanonické rovná sa.
Rozmіrkovuєmo podobne predtým, ako pri poslednej elіpse.
1. Poznáme priesečníky s osami hyperboly. Ak x = 0, potom . Krapok peretina z vsyu OU nie je. Ak y = 0, potom . Reline body, . Smrdí sú tzv vrcholy hyperbol.
2. Oblasť rozšírenia hyperboly: tobto. alebo . To znamená, že hyperbola je rozstrapatená snežnou pózou, obklopená rovnými čiarami. x=-aі x = a.
3. Hyperbolu možno vidieť v celej symetrii, pretože x i y vstupujú do dvojitých krokov. Stačí mu pozrieť sa na tú časť hyperboly, ako keby bola schovaná v prvej štvrtine.
4. Rovnica hyperboly (2) v prvom štvrťroku mesiaca. Keď x \u003d a, y \u003d 0, existuje bod; o , potom. zákruta choďte do kopca doprava. Aby to bolo jasnejšie, môžeme sa pozrieť na dve ďalšie priame čiary, tj prejsť cez klas súradníc i є uhlopriečky obdĺžnika so stranami 2a a 2b: BCB'C'. Zápach môže byť rovnaký. Dá sa ukázať, že aktuálny bod hyperboly M(x, y), ktorý sa dostane do nekonzistentnosti, sa bez prekážok približuje k priamke. Vezmite dobrý bod X a porіvnyaєmo vіdpovіdnі súradnice bodu hyperboly a - priamka. Očividne čo Y>y. MN=Y-y=.
Bachimo, scho, tobto. krivka je blízko k priamke vo svete vo vzdialenosti od klasu súradníc. Tse priniesť, scho je priama asymptota hyperboly. Navyše hyperbola nemení asymptoty. Čo stačí, vzbudiť časť hyperboly. Vaughn je brutálne na kopci. Ostatné časti sa získajú symetriou. Je dôležité, aby sa osi symetrie hyperboly (súradnicové osi) nazývali її osi, bod osí- stred hyperbola. Jedna celá peretinaє hyperbola (dіysna vіs), іnsha-ni (vyavna). Vіdrіzok a nazvite to diysnoy pivvissya, vіdrіzok b-zrejmé pivvissyu. Obdĺžnik BCB'C' sa nazýva hlavný obdĺžnik hyperboly.
Yakscho a=b, potom asymptoty spĺňajú súradnicové osi kuti . Rovnaká hyperbola alebo hovor rovný alebo rovný. Hlavný obdĺžnik sa zmení na štvorec. Asymptoty її sú kolmé na jednu samotnú.
Rešpekt.
Niekedy sa pozerajú na hyperbolu, ktorá sa kanonicky rovná - (3). Її meno zviazaný odkazom na hyperbolu (2). Hyperbola (3) môže byť vertikálne vertikálna, zrejmá-horizontálna. Її pohľad sa okamžite obnoví, akoby sa preusporiadal Xі pri, aі b(Premení sa na kolos). Ale tody hyperbola (3) môže vyzerať:
Vrcholy її.
5. Ako už bolo uvedené, rovnaká rovnostranná hyperbola ( a = b) ak osi súradníc zbіgayutsya s osami hyperboly, môže vyzerať. (4)
Pretože asymptotiky rovnostrannej hyperboly sú kolmé a možno ich brať aj ako súradnicové osi OX 1 a OU 1 . Stojí za to obrátiť kolosálny systém OXY do rezu. Vzorce na zapnutie rezu sú:
Todi v nový systém súradnice OX 1 Y 1 rovné (4) prepíšte:
Abo abo. Významne, otrimaemo alebo (5) cena rovnostranná hyperbola, zredukované na asymptoty (rovnaký druh hyperboly bol videný v škole).
Rešpekt S = k 2 .
7. Vymenovanie a definícia kanonického zarovnania paraboly.
parabola nazývaný GMT oblasti, pre kožu zameranie. riaditeľka(Sústredný postoj riaditeľky).
Je príznačné, že rozdiel medzi F a priamkou cez p sa nazýva parameter paraboly. Vyberieme nasledujúci súradnicový systém: všetky OX sa tiahnu cez bod F kolmý na priamku NP. Klas súradníc je viberálne v strede klinu FP.
Pre môj systém: .
Zoberme si dodatočný bod M(x, y) z aktuálnych súradníc (x, y). Tom
Zvіdsi (1) tse i є rivnyannya parabola. Povedzme len:
Abo (2) -ce i є kanonické zarovnanie paraboly Môžete ukázať, že (1) a (2) sú rovnaké.
Vlastné imanie (2) sa rovná 2. rádu, tobto. parabola-čiara 2. rádu.
8. Doslіdzhennya formy paraboly pre її kanonické rovná.
(p>0).
1) x=0, y=0 parabola prechádza klasom súradníc bodom O. Її sa nazýva vrchol paraboly.
2), potom. parabola je otočená doprava od osi OS, na pravej strane roviny.
3) pri vstúpiť do párového sveta, parabola je symetrická k tomu, ako je os OH, potom to urobiť v prvej štvrtine.
4) o 1 štvrťroku o , potom. parabola ísť pravou rukou. Môžete mi ukázať, že idem do kopca. Podľa symetrie budem nižšie. Všetky OU sú dotichna do bodu paraboly.
Je zrejmé, že ohniskový polomer je . Nastavenie je tzv výstrednosť: . Všetka symetria paraboly (máme OH) sa nazýva celá parabola.
S úctou, zarovnanie je tiež parabola, ale je narovnané do opačného biku. Rivnyannya tiež nastaviť paraboly, všetky yakikh є všetky OU.
alebo pri väčšom zvichnomu pohľade, de.
Rivnyannia znamená veľkú parabolu s posunutým vrcholom.
Rešpekt. 1) Mіzh usima chotirma s líniami 2. rádu je blízko sporu; konečné rezy. Ak vezmete kužeľ z dvoch prázdnych, potom keď ho prerežete rovinou kolmou na os kužeľa, vezmete kolík, ako trio rán, prerežte oblasť cez rez; ak je rovina rovnobežná s lichotivou, tak v obvode je parabola, ak rovina pretvára priestupok
prázdno-hyperbola.
2) Dá sa vyniesť na svetlo, že ak svetlo vyjde mimo ohnisko paraboly, objaví sa v nej, potom svetlo ide rovnobežne s osou parabolického-tse, aby vyhralo, keď sú projektory parabolicko-parabolické, a pri ohnisku-dzherelo svetlo. Ak chcete vyjsť rovnanie potіk svіtla.
3) Ako zistiť štart družice Zeme z bodu T, ktorý má ležať v atmosfére vo vodorovnej línii, ako keby sa klas pozametal. v 0 nedostatok, potom sa spoločník neobíde okolo Zeme. Pri dosiahnutí prvého vesmírneho letu sa satelit otočí okolo Zeme po kruhovej dráhe so stredom v strede Zeme. Ak chcete zväčšiť šírku klasu, potom bude obal elipsa, stred Zeme bude v jednom z ohniskov. Pri dosiahnutí 2. vesmírneho letu sa trajektória stane parabolickou a satelit sa neotočí do bodu T, ale zmeníme hranice Systém Sonyachna. Tobto. Parabola є elips s jedným nekonečne vzdialeným ohniskom. S ďalším zvýšením rýchlosti klasu sa trajektória stane hyperbolickou a z druhej strany sa objaví ďalšie ohnisko. Stred Zeme je počas celej hodiny v ohnisku obežnej dráhy. Companion pіde pre mezhі Sonyachnі systém.
Prednášky z algebry a geometrie. 1. semester
Prednáška 15. Elips.
Rozdil 15. Elips.
položka 1. Hlavné stretnutie.
Vymenovanie. Elipsa je GMT oblasti súčtu až dvoch pevných bodov oblasti, nazývaných ohniská, a je to konštantná hodnota.
Vymenovanie. Vzdialenosť od malého bodu roviny M k ohnisku elipsy sa nazýva ohniskový polomer bodu M.
Označenie:  - triky elipsy,
- triky elipsy,  - Polomery ohniska bodu M.
- Polomery ohniska bodu M.
Pre účely elipsy je bod M bodom elipsy a potom, ak  - Konštantná hodnota. Qiu postiynu sa považuje za 2a:
- Konštantná hodnota. Qiu postiynu sa považuje za 2a:
 .
(1)
.
(1)
Rešpektujeme to  .
.
Pre účely elipsy je jej ohniskom fixácia bodu, takže pre túto elipsu existuje konštantná hodnota.
Vymenovanie. Stojan medzi ohniskami elipsy sa nazýva ohnisková vzdialenosť.
Označenie:  .
.
3 trikutník  kričať čo
kričať čo  , potom.
, potom.
 .
.
Výrazne cez b je číslo, ktoré je drahé  , potom.
, potom.
 .
(2)
.
(2)
Vymenovanie. Nastavenie
 (3)
(3)
nazývaná excentricita elipsy.
Na tejto rovine zavedieme súradnicový systém, ktorý sa pre elipsu nazýva kanonický.
Vymenovanie. Celok, na ktorom leží ohnisko elipsy, sa nazýva ohnisko.
Buďme kanonickí pre PDSC Ellipse, div. obr.2.
Ako os x zvolíme ohniskovú os a celá ordináta sa nakreslí cez stred vdrіzky.  kolmo na ohniskovú os.
kolmo na ohniskovú os.

Stačí sa zamerať na súradnice  ,
,
 .
.
položka 2. Kanonická rovnosť elipsy.
Veta. Kanonický súradnicový systém pre elipsu má zarovnanie elipsy môže vyzerať takto:
 .
(4)
.
(4)
Prinášanie. Dokazovanie bude prebiehať v dvoch etapách. V prvej fáze vieme, že súradnice akéhokoľvek bodu, ktorý leží na elipse, vyhovujú zarovnaniu (4). V ďalšej fáze budeme vedieť povedať, či riešenie (4) udáva súradnice bodu, ktorý leží na elipse. Zvіdsi vyplivatime, scho sa rovná (4) spĺňa ti a ti body súradnicovej roviny, rád leží na elіpsі. Zvіdsi i vyznachennya іvnyannja krivoї sіduvat, shko іvnyannja (4) є іvnyannâ elіpsa.
1) Nech bod M (x, y) je bodom elipsy, tobto. súčet її ohniskových polomerov je 2а:
 .
.
Zrýchlime vzorec medzi dvoma bodmi na súradnicovej rovine a poznáme vzorec pre ohniskový polomer daného bodu M:
 ,
,
 , hviezdy sa berú:
, hviezdy sa berú:
Presuňme jeden odmocninec do pravej časti vyrovnanosti a hviezdičku do štvorca:
Rýchlo, otrimuemo:
Navrhujeme podobne, krátko na 4 a usamіtnyuemo radikálne:
 .
.
Zvodimo na námestí
Otváranie oblúkov a rýchlo ďalej  :
:
hviezdy sú vítané:
Vicorist rіvnіst (2), otrimuemo:
 .
.
Po rozdelení zvyšku žiarlivosti ďalej  , Požadovaná vyrovnanosť (4) atď.
, Požadovaná vyrovnanosť (4) atď.
2) Nech teraz dvojica čísel (x, y) vyhovuje zarovnaniu (4) a nech M(x, y) – príslušný bod na súradnicovej rovine Oxy.
Témy (4) sú jasné:
 .
.
Nahradením polomerov ohniska bodu M rovnovážnosťou:

 .
.
Tu nás oživila žiarlivosť (2) a (3).
takýmto spôsobom,  . podobne,
. podobne,  .
.
Teraz je úctivé, že zo žiarlivosti (4) kričíš
 alebo
alebo  a preto
a preto  , potom je tu očividný nepokoj:
, potom je tu očividný nepokoj:
 .
.
Zvіdsi, po tvojom boku, kričí, scho
 alebo
alebo  і
і
 ,
,
 .
(5)
.
(5)
Tri rovnosti (5)  , potom. bod M(x, y) je bodom elipsy atď.
, potom. bod M(x, y) je bodom elipsy atď.
Veta bola dokončená.
Vymenovanie. Zarovnanie (4) sa nazýva kanonické zarovnanie elipsy.
Vymenovanie. Kanonické osi súradníc elipov sa nazývajú hlavové osi elipov.
Vymenovanie. Klas kanonického súradnicového systému pre elipsu sa nazýva stred elipsy.
položka 3. Dominancia elipsy.
Veta. (Sila elipsy.)
1. Kanonický súradnicový systém pre elipsu, všetky
body elipsy sa nachádzajú v blízkosti obdĺžnika
 ,
,
 .
.
2. Krapki ležia na
3. Elіps є krivka, symetrické shdo
vlastné osky hlavy
4. Stred elipsy je stredom symetrie.
Prinášanie. 1, 2) Vidíte kanonické zarovnanie elipsy.
3, 4) Nech M (x, y) - dostatočný bod elipsy. Potom sú súradnice spokojné so zarovnaním (4). Potom sú však súradnicové body spokojné aj so zarovnaním (4), i, aj s bodmi elipsy, hviezdami a dôkazom vety.
Veta bola dokončená.

Vymenovanie. Hodnota 2a sa nazýva veľká váha elipsy, hodnota sa nazýva veľká váha elipsy.
Vymenovanie. Hodnota 2b sa nazýva malá váha elipsy, hodnota b sa nazýva malá váha elipsy.
Vymenovanie. Škvrny pavučiny elipsy s osami hlavy sa nazývajú vrcholy elipsy.
Rešpekt. Týmto spôsobom možno povzbudiť elipsy. Na byte v blízkosti ohniska "zatĺkame na kvety" a pripevníme na ne závit zavdovky  . Vezmeme si olivu a s pomocou potiahneme niť. Potom prevlečieme olivové pero po ploche, prešívame za ňou, aby bola niť napnutá.
. Vezmeme si olivu a s pomocou potiahneme niť. Potom prevlečieme olivové pero po ploche, prešívame za ňou, aby bola niť napnutá.
Z pohľadu excentricity to vidíme

Opravíme číslo a a nasmerujeme číslo od nuly. Todi at  ,
,
 і
і  . Medzi nami je to prijateľné
. Medzi nami je to prijateľné
 alebo
alebo  - Rovnaký podiel.
- Rovnaký podiel.
Priamo teraz  . Todi
. Todi  ,
,
 a mi bachimo, že medzi elepmi virodzhuєtsya na vіdrіzok priamky
a mi bachimo, že medzi elepmi virodzhuєtsya na vіdrіzok priamky  mať malé dieťa 3.
mať malé dieťa 3.
položka 4. Parametrické zarovnanie elipsy.
Veta. Poď  - Prevіlnі dіysnі čísla. Rovnaké vyrovnávanie systému
- Prevіlnі dіysnі čísla. Rovnaké vyrovnávanie systému
 ,
,
 (6)
(6)
є parametrické vyrovnania kanonickej elipsy pre súradnicový systém elipsy.
Prinášanie. Dosit, aby sa systém rovnal (6) є rovný rovný (4), tobto. smrad mayut tie iste neosobne riesenie.
1) No tak (x, y) - dostatočné riešenie sústavy (6). Rozdeľme prvý rovný na a, druhý - na b, rozdelíme rovnaký štvorec a pridáme:
 .
.
Tobto. či je riešenie (x, y) sústavy (6) splnené s rovnicou (4).
2) Späť, nech sa pár (x, y) є rozhodnutia rovná (4), tobto.
 .
.
Z tsієї rіvnostі viplivaє, súradnice scho bodu z  ležať na dĺžke jedného polomeru so stredom na klase súradníc, tj. є bod trigonometrického kolíka
ležať na dĺžke jedného polomeru so stredom na klase súradníc, tj. є bod trigonometrického kolíka  :
:

Z pohľadu sínusu a kosínusu je to hneď zrejmé
 ,
,
 , de
, de  , nasledujú hviezdičky, aká dvojica (x, y) sú riešenia sústavy (6) atď.
, nasledujú hviezdičky, aká dvojica (x, y) sú riešenia sústavy (6) atď.
Veta bola dokončená.
Rešpekt. Elipsy môžu byť prijaté ako výsledok rovnakého "stlačenia" kolíka s polomerom a k osi x.
Poď  - Zarovnanie kolíka so stredom klasu súradníc. "Stisk" kolíka k osi x nie je nič iné, ako transformácia súradnicovej roviny, ktorá sa riadi nasledujúcim pravidlom. Bod kože M(x, y) je nastavený v bode roviny
- Zarovnanie kolíka so stredom klasu súradníc. "Stisk" kolíka k osi x nie je nič iné, ako transformácia súradnicovej roviny, ktorá sa riadi nasledujúcim pravidlom. Bod kože M(x, y) je nastavený v bode roviny  , de
, de  ,
,
 - Koeficient "stlačenia".
- Koeficient "stlačenia".

Pri akejkoľvek transformácii sa kožný bod kolíka "premiestňuje" do iného bodu roviny, čo tvorí samotnú úsečku, ale zmenšuje ordinátu. Virasimo stará súradnica bodu cez novú:

a môžu byť zastúpené v rovnakom podiele:
 .
.
Vezmite prosím na vedomie:
 .
(7)
.
(7)
Môžete vidieť, že pred transformáciou "stláčania" ležal bod M (x, y) na kolíku, tobto. її súradnice boli spokojné s úrovňou stávky, potom po transformácii „stlačenia“ bod „prešiel“ do bodu  súradnice, ktoré spĺňajú zarovnanie elipsy (7). Ak chceme vziať vyrovnanie elipsy z malého pіvvіssyu b, je potrebné vziať koeficient kompresie
súradnice, ktoré spĺňajú zarovnanie elipsy (7). Ak chceme vziať vyrovnanie elipsy z malého pіvvіssyu b, je potrebné vziať koeficient kompresie
 .
.

položka 5. Stosovno elіpsa.
Veta. Poď  - Pekná bodka elipsy
- Pekná bodka elipsy
 .
.
Todi sa rovná tsієї elіpsu v bodoch  môže vyzerať:
môže vyzerať:
 .
(8)
.
(8)
Prinášanie. Stačí sa pozrieť na sklon, ak torzný bod leží v prvej alebo druhej štvrtine súradnicovej roviny:  . Zarovnanie elipsy v hornej časti najvyššieho poschodia môže vyzerať takto:
. Zarovnanie elipsy v hornej časti najvyššieho poschodia môže vyzerať takto:
 .
(9)
.
(9)
Rýchlo prispôsobíme harmonogram funkcie  v bode
v bode  :
:
de  - hodnota podobnej funkcie v bode
- hodnota podobnej funkcie v bode  . Elipsy v prvom štvrťroku možno vidieť ako funkčný graf (8). Vieme, že її pokhіdnu її, že її znachenya v bode dotik:
. Elipsy v prvom štvrťroku možno vidieť ako funkčný graf (8). Vieme, že її pokhіdnu її, že її znachenya v bode dotik:
 ,
,
 . Tu sme sa k sebe túlili, aký zmysel má týranie
. Tu sme sa k sebe túlili, aký zmysel má týranie  є bod elipsy a її súradnice spĺňajú zarovnanie elipsy (9), tzn.
є bod elipsy a її súradnice spĺňajú zarovnanie elipsy (9), tzn.
 .
.
Uvádzame známu hodnotu podobnej rovnej bodky (10):
 ,
,
hviezdy sú vítané:
Zvuky kričia:
Rozdeľme túto žiarlivosť na  :
:
 .
.
Stratila som rešpekt, scho  , pretože strakatý
, pretože strakatý  ležať na elіpsu a її súradnice sú spokojní s jogou rovná.
ležať na elіpsu a її súradnice sú spokojní s jogou rovná.
Podobne sa dosiahne zarovnanie bodky (8) v bode bodík, ktorý leží v tretej alebo štvrtej štvrtine súradnicovej roviny.
І, nareshti, ľahko perekonuєmosya, scho vyrovnanie (8) dáva bodové vyrovnanie v bodoch  ,
,
 :
:
 alebo
alebo  , і
, і  alebo
alebo  .
.
Veta bola dokončená.
položka 6. Zrkadlová sila elipsy.
Veta. Dotychna to elіpsa maє rovnaké cuti s ohniskovými polomermi torzného bodu.

Poď  - torzný bod,
- torzný bod,  ,
,
 - ohniskové polomery bodu dotik, P a Q - projekcie ohniskov na bod, vykreslené do elipsy v bode
- ohniskové polomery bodu dotik, P a Q - projekcie ohniskov na bod, vykreslené do elipsy v bode  .
.
Veta to dokazuje
 .
(11)
.
(11)
Túto vyrovnanosť možno interpretovať ako vyrovnanosť pádu a fermentáciu svetla v podobe elipsy, uvoľnenej z jogového ohniska. Tsya power získala názov zrkadlovej sily elipsy:
Po zhliadnutí prechodu zrkadla elipsy cez druhé ohnisko elipsy uvoľnite svetlo z ohniska elipsy.
Dôkaz vety. Na dôkaz ekvivalencie kutiv (11) prinášame podobnosť trikutnikov  і
і  , ktorým smerom
, ktorým smerom  і
і  bude podobný. Oskіlki trikutnika rovného strihu, stačí priniesť rovnocennosť
bude podobný. Oskіlki trikutnika rovného strihu, stačí priniesť rovnocennosť
 .
(12)
.
(12)
Na prebudenie  - Pozrite sa rozostrený
- Pozrite sa rozostrený  na bod L (oddiel obr. 7),
na bod L (oddiel obr. 7),  . Zrýchlenie vzorca z bodu na priamku v rovine:
. Zrýchlenie vzorca z bodu na priamku v rovine:
Nakoľko sa teda bodka elipsy zhoduje s bodkou  môže vyzerať
môže vyzerať
 ,
,
 ,
,

 .
.
Tu sme použili vzorce (5) pre ohniskové polomery bodu elipsy.
Veta bola dokončená.
Ďalší dôkaz vety:
 ,
,
 ,
,
 - Normálny vektor dotického L.
- Normálny vektor dotického L.
 . Zvіdsi,
. Zvіdsi,  .
.
Podobne vieme  і
і  , Ch.t.d.
, Ch.t.d.
položka 7. Adresáre Ellipse.
Vymenovanie. Smerové čiary elіps sa nazývajú dve priame čiary, ktoré sa môžu rovnať v kanonickom súradnicovom systéme pre elips
 alebo
alebo  .
(13)
.
(13)

Veta. No tak M - dostatočný bod elipsy,  ,
,
 - її ohniskové polomery,
- її ohniskové polomery,  - Choďte z bodu M k ľavej smerovej čiare,
- Choďte z bodu M k ľavej smerovej čiare,  - Doprava. Todi
- Doprava. Todi
 ,
(14)
,
(14)
de  - Výstrednosť elipsy.
- Výstrednosť elipsy.
Prinášanie.

Dajme si M(x, y) - súradnice čiastkového bodu elipsy. Todi
 ,
,
 ,
,
hviezdy a volajte po vyrovnanosti (14).
Veta bola dokončená.
položka 8. Ohniskový parameter elipsy.
Vymenovanie. Ohniskovým parametrom elipsy je dĺžka kolmice, ktorá je predĺžená od ohnísk až po priamku s elipsou.
Ohniskový parameter sa označuje písmenom.

Je dôležité vedieť, aký je ohniskový parameter
 .
.
Veta. Ohniskový parameter elipsy je viac
 .
(15)
.
(15)
Prinášanie. Takže bod N (-c; p) je bodom elipsy  , potom sú її súradnice spokojné s jeho zarovnaním:
, potom sú її súradnice spokojné s jeho zarovnaním:
 .
.
Zvіdsi vedia
 ,
,
hviezdy ďalej (15).
Veta bola dokončená.
položka 9. Iné označenie elipsy.
Veta і z bodu 7. môžete použiť elіpsa.
Vymenovanie. Elipsa je GMT pre akúkoľvek vzdialenosť k pevnému bodu roviny, nazývanému ohnisko, k vzdialenosti k pevnej priamke, nazývanej priamka, konštantná hodnota menšia ako jedna, nazývaná excentricita:
 .
.

Je zrejmé, že v časoch, predtým, než je vymenovanie eooips vetou, je potrebné ju uviesť.
Vstup
Predtým boli krivky iného rádu skrútené jedným z Platónovho učenia. Yogo robot strčil do ofenzívy: ak vezmete dve rovné čiary, ktoré sú prepletené, a obtočíte ich okolo nimi stanovenej osy kutu, potom je weide kužeľová plocha. Ak prevrátite povrch rovným povrchom, potom budú rozdiely v obvode geometrické tvary, A tie isté elipsy, kolo, parabola, hyperbola a šprot virogénnych figúrok.
Vedecké poznatky však v 17. storočí vedeli menej, ak sa zistilo, že planéty sa rúcajú po eliptických trajektóriách a harmonický projektil letí parabolicky. Ešte horšie bolo vedieť, že na to, aby telo dostalo prvú kozmickú silu, zrúti sa na kôl v blízkosti Zeme, so zvýšením sily sily - elipsou a po dosiahnutí ďalšej kozmickej sily tela o parabola, zbaviť gravitačné pole.
Elіps ta yogo rivnyannia
Vymenovanie 1. Neosobný bod v rovine sa nazýva elipsa;
Ohniská elipsy sú označené písmenami a medzi ohniskami - cez a súčtom súčtu bodov elipsy do ohniska - cez. Okrem toho 2a > 2c.
Kanonické vyrovnanie elipsy môže vyzerať:
de pov'yazanі mіzh i vіvnіstyu a 2 + b 2 \u003d c 2 (alebo b 2 - a 2 \u003d c 2).
Veľkosť sa nazýva veľká váha a malá váha elipsy.
Označenie 2. Excentricita elipsa sa nazýva prechod medzi ohniskami až po starú veľkú os.
Označuje sa písmenom.
Črepy pre menovania 2a>2c, excentricita je vždy vyjadrená ako vlastný zlomok, tj. .
Vymenovanie 7.1. Veľa všetkých bodov v rovine, pre akýkoľvek súčet až dvoch pevných bodov F 1 a F 2 є je daná konštantná hodnota, tzv. elipsa.
Označenie elipsa dáva takémuto spôsobu jogy geometrickú inšpiráciu. Je fixovaná v rovine dvoch bodov F 1 a F 2 a nepostrehnuteľná konštantná hodnota je významná cez 2a. Presuňme sa medzi bodmi F1 a F2 až po 2c. Je zrejmé, že nenatiahnutá niť s dvojitým 2a je upevnená v bodoch F 1 a F 2 napríklad za pomocou dvoch hláv. Uvedomil som si, že je to možné len pre a ≥ c. Po potiahnutí nite olivou sme preťali čiaru, ako keby to bola elipsa (obr. 7.1).
Otzhe, multiplikátor nie je prázdny, yakscho a ≥ s. Keď a \u003d prekročí є vіdrіzok z kіntsami F 1 a F 2, a keď c \u003d 0, potom. kde sú pevné body upevnené na určenej elipse, vin je blízko polomeru a. Vzhľadom na to, že na jeseň sú virogény, budeme musieť odhadnúť, že > z > 0.
Upevňovacie body F 1 a F 2 v určených elipsách 7.1 (div. obr. 7.1) sú tzv. elipsové triky, medzi nimi, označené cez 2c, - ohnisko a šípky F 1 M a F 2 M, ktoré dostatočne blízko bodu M na elipse svojimi ohniskami, - ohniskové polomery.
Vidieť elіpsa je pravdepodobnejšie ústredným bodom | Ž 1 Ž 2 | \u003d 2 s parametrom і a, ako poloha v rovine - dvojica bodov F 1 і F 2 .
Označenie elipsy je jasné, aby bola žila symetrická ako rovná, ako prechádzať ohniskami F 1 a F 2, ako aj ako narovnať, ako rozdeliť altánok F 1 F 2 navpil і kolmo na yoma (obr. 7.2 a). Qi priamy názov osi elipsy. Bod O їх brvno є stred symetrie elipsov a її hovor stred elipsy, A body priamky elipsy s osami symetrie (body A, B, C a D na obr. 7.2, a) - elipsovité vrcholy.

Pomenujte číslo skvelé pіvvіssyu elіps, a b = √(a 2 - c 2) - joga malý pіvvіssyu. Nie je dôležité poznamenať, že pre c > 0 je vzdialenosť od stredu elipsy veľká k pokojným vrcholom, pretože sú na rovnakej osi s ohniskami elipsy (vrcholy A a B na obr. 7.2 a ) a vzdialenosť od stredu je malá k dvom ďalším vrcholom (vrcholom C a D na obr. 7.2, a).
Rivnyannia elips. Pozrime sa na plochú elipsu s ohniskami v bodoch F 1 a F 2 veľkej oblohy 2a. No tak 2c - ohnisková vzdialenosť, 2c = | F1F2 |
Vyberieme pravouhlý súradnicový systém Oxy v rovine tak, aby klas spivpav іz stred elipsy a ohniská boli na vodorovná os(obr. 7.2, b). Tento súradnicový systém je tzv kanonický pre analyzovanú elipsu a ostatné zmeny - kanonický.
Pre zvolený súradnicový systém môžu byť ohniskom súradnice F 1 (c; 0), F 2 (-c; 0). Vikoristovuyuchi vzorec vіdstanі mіzh body, zapíšte si myseľ | F 1 M | + | F 2 M | = 2a v súradniciach:
√((x - c) 2 + y 2) + √ ((x + c) 2 + y 2) = 2a. (7,2)
Tsіvnyannya nie je po ruke, na to sú v novom dva štvorcové radikály. Preto robme jogu. Prevedenie na rovnaký (7.2) ďalší radikál y do pravej časti a štvorec hviezdy y:
(x - c) 2 + y2 = 4a 2 - 4a√((x + c) 2 + y 2) + (x + c) 2 + y2.
Po otvorení luku a prinášaní podobných dodankіv otrimuєemo
√((x + c) 2 + y 2) = a + εx
de ε = c/a. Opakujeme kvadratúru, aby sme získali i ďalší radikál: (x + c) 2 + y 2 = a 2 + 2εax + ε 2 x 2 alebo so zmenou hodnoty zavedeného parametra ε, (a 2 - c 2) x 2 /a2 + y2 = a2-c2. Skіlki a 2 - c 2 \u003d b 2\u003e 0, potom
x 2 /a 2 + y 2 /b 2 = 1, a > b > 0. (7.4)
Zarovnanie (7.4) vyhovuje súradniciam všetkých bodov, ktoré ležia na elipse. Ale pri odvodzovaní víťazného vyrovnania došlo k neekvivalentným permutáciám vonkajšieho vyrovnania (7.2) - dve štvorcové väzby, ktoré preberajú štvorcové radikály. Jednotky sa rovnajú štvorcu є ekvivalentom transformácií, takže v oboch jeho častiach sú hodnoty v rovnakom znamienku, nezmenili alchýmiu vo svojich transformáciách.
Nemôžeme premýšľať o ekvivalencii transformácie, ako keby to bolo nesprávne. Dvojica bodov F 1 a F 2 | Ž 1 Ž 2 | \u003d 2c, roviny definujú rodinu elips s ohniskami v týchto bodoch. Kožný bod roviny, okrajový bod vіrіzka F 1 F 2 ležať ako elіpsu určenej rodiny. V žiadnom čase sa dve elipsy neprekrývajú, črepy súčtu ohniskových polomerov jednoznačne naznačujú konkrétnu elipsu. Neskôr je opísaná rodina elips bez premostenia, pokrývajúca celú plochu, karmínový bod F1F2. Pozrime sa na neosobné body, ktorých súradnice spĺňajú zarovnanie (7.4) s hodnotami parametra a. Čo môže veľa rozpodіlyatisya medzi kіlkom elipsami? Časť bodov multiplikátora leží na elіpsu s veľkým pіvvіssya a. Nech je bod v tejto mnohosti, ktorý leží na elipse z veľkej pivvissye. Potom sú súradnice bodov zoradené rovnako
tobto. ekvivalencie (7.4) a (7.5) môžu mať veľké rozhodnutia. Je však ľahké sa nechať zmiasť, že systém

pre ã ≠ a neexistuje riešenie. Pre koho stačí zahrnúť napríklad x z prvého rovnakého:

scho po prepracovaní vychovať rovných

nevie sa rozhodnúť, keď ã ≠ a, čriepky. Tiež (7.4) є vyrovnanie elipsy s veľkým pіvvіssyu a > 0 і malým pіvvіssyu b = √ (a 2 - c 2) > 0. na kanonické rovné elipsy.
Recenzia elipsy. Pokročilejší geometrický spôsob povzbudenia elіpsa poskytuje dostatočné informácie o staromódny elipsa. Ale, typ elіps môže byť potvrdený a pomocou jogovej kanonickej ekvivalencie (7.4). Napríklad, ak vezmeme do úvahy y ≥ 0, môžete sa pozrieť cez x: y \u003d b√ (1 - x 2 / a 2), i, po vykonaní tejto funkcie, indukovať її graf. Existuje ešte jeden spôsob, ako vyvolať elipsu. Stĺpec s polomerom a so stredom na klase kanonického súradnicového systému elipsy (7.4) je opísaný rovnosťami x 2 + y 2 = a 2 . Ako її stlačiť s koeficientom a / b > 1 vzdovzh osi ordinátov, potom vytvorte krivku, ako je opísaná ako rovná sa x 2 + (ya/b) 2 = a 2 potom elipsy.
Rešpekt 7.1. Ako stlačíte rovnaké množstvo pomocou koeficientu a / b
Výstrednosť elipsy. Predĺženie ohniskovej vzdialenosti elipsy k veľkej osi je tzv elipsová výstrednosť a označte ε. Pre danú elipsu

kanonické rovnosti (7.4), ε = 2c/2a = с/a. Ako (7.4) parametre a a b súvisia s nekonzistentnosťou a
S c = 0, ak sa elіps transformuje na kruh, i ε = 0. V ostatných prípadoch 0
Rovnica (7.3) sa rovná rovno (7.4), črepy sa rovnajú (7.4) a (7.2) . Elipsa sa rovná tej (7.3). Okrem toho, spіvvіdnoshennia (7.3) cіkave tim, scho dáva jednoduchý, nepomstia radikály, vzorec pre dozhini | F 2 M | jeden z polomerov ohniska bodu M(x; y) elipsy: | F 2 M | = a + εx.
Podobný vzorec pre iný ohniskový polomer je, že ho možno odobrať zo symetrie opakovaní inlayov, v ktorých je prvý radikál prenesený na pravú stranu a nie druhý. Tiež pre ľubovoľný bod M(x; y) na elіpsі (del. Obr. 7.2)
|F 1 M | = a - ?x, | F 2 M | = a + εx, (7,6)
a koža z tsikh rivnyan є elipsa rovnaké.
Príklad 7.1. Poznáme kanonické zarovnanie elipsy s veľkým pіvvіssyu 5 a excentricitou 0,8 a bude yogo.
Keď poznáme veľké pіvvіs elіps a = 5 a excentricitu ε = 0,8, poznáme malé pіvvіs b. Oskilki b \u003d √ (a 2 - z 2) a c \u003d εa \u003d 4, potom b \u003d √ (5 2 - 4 2) \u003d 3. Znamená to kanonicky rovnaký vzhľad x 2 / 5 2 + y 2 / 3 2 \u003d 1. Ak chcete vytvoriť elipsu, manuálne nakreslite obdĺžnik so stredom na klas kanonického súradnicového systému, ktorého strany sú rovnobežné s osami symetrie elipsy a sú zarovnané s príslušnými osami (obr. 7.4). Tsei rectocart sa hrá s

osi elіps vo svojich vrcholoch A(-5; 0), B(5; 0), C(0; -3), D(0; 3), navyše samotný elіps má položky new. Na obr. 7.4 tiež indikovali ohniská F 1,2 (±4; 0) elipsy.
Geometrická mocnosť elipsy. Prepíšme skoršie rovné (7.6) vzhľadom na |F 1 M| = (a/ε - x)ε. Je príznačné, že hodnota a / ε - x pre a > h je kladná, ale ohnisko F 1 neleží v elipse. Hodnota Tsya є k zvislej priamke d: x \u003d a / ε v bode M (x; y), ktorý by mal ležať ľavou rukou v smere priamky. Rivnyannya elіpsa môže byť napísaná pri pohľade
|F1M|/(a/ε - x) = ε
Znamená to, že tento elips je zložený z pokojných bodov M (x; y) roviny, pre ktoré je predĺženie ohniskového polomeru F 1 M na priamku d konštantnou hodnotou, ktorá je väčšia ε (obr. 7.5) .

Priamka d є "dvіynik" - zvislá čiara d", je symetrická k d ako stred elipsu, takže x = -a / ε sa rovná. Priestupky priamo d a d meno režiséri elipsy. Riadidlá elipsy sú kolmé na os symetrie elipsy, na akomsi zaostrení ohnísk, a stoja v strede elipsy vo vzdialenosti a/ε = a 2 /c (rozdiel obr. 7.5).
Vіdstan p vіd directrix k najbližšiemu jej zameraniu sa volá ohniskový parameter elipsov. Tento parameter je drahší
p \u003d a / ε - c \u003d (a 2 - c 2) / c \u003d b 2 / c
Elips je ďalšia dôležitá vec geometrická sila: ohniskové polomery F 1 M a F 2 M sa sčítavajú od bodu po elipsy v bode M sa rovnajú cuti (obr. 7.6).

Tsya vlastіvіst maє naochny fіzichny zmіst. Ak má ohnisko F 1 vzplanutie svetla, tak je čas ísť mimo ohnisko, po dopade na elipsu po inom ohniskovom polomere, teda po dopade na víno zmeníme rovnaký rez na krivku, potom k zásahu. Takto sa všetky zmeny, ktoré vychádzajú z ohniska F 1, sústreďujú do iného ohniska F 2 a rovnakým spôsobom. Z tohto výkladu sú úrady priradené k názvu optická mohutnosť elipsy.
Krivky v inom poradíčiary sa nazývajú na rovine, ktoré sú označené rovná sa, v niektorých meniacich sa súradniciach Xі r urobiť krok ďalším krokom. Pred nimi je vidieť elipsy, hyperbolu a parabolu.
Zagalny pohľad na krivku iného rádu:
de A B C D E F- čísla a chcieť byť jedným z koeficientov A, B, C nerovná sa nule.
Keď je poradie obrátené z kriviek iného rádu, najčastejšie je vidieť kanonické zarovnanie elipsy, hyperboly a paraboly. Je ľahké prejsť k nim v horných úrovniach, ku ktorým bude priradený zadok 1 úloh s elipsami.
Elіps, priradenia kanonickým rovným
Menovaná elipsa. Elipsa je bezmenný krátky bod roviny, takže pre určitú vzdialenosť k bodom nazývaným ohniská je konštantná hodnota a väčšia, nižšia medzi ohniskami.
Ohniská sú označené ako trochu nižšie.
Kanonické vyrovnanie elipsy môže vyzerať:
de aі b (a > b) - Dovzhini pіvosey, to znamená polovice dovzhin vіdrіzkіv, ktoré sú znázornené ako elipsy na súradnicových osiach.

Priama čiara, ktorá prechádza ohniskami elipsy, má rovnakú symetriu. Druhá polovica symetrie elipsy je rovná, ktorá prechádza stredom rebra kolmo na toto rebro. Krapka Pro Peretínové čiary tsikh slúžia ako stred symetrie elipsy alebo jednoducho stred elipsy.
Všetky úsečky sa prekladajú v bodoch ( a, Pro) ta (- a, Pro), a všetky súradnice - v bodoch ( b, Pro) ta (- b, Pro). Počet bodov sa nazýva vrcholy elipsy. Hrebeň medzi vrcholmi elipsy na osi x sa nazýva veľký vrchol a na osi y - malý vrchol. Hrebene od vrchu po stred elipsy sa nazývajú čapíky.
Yakscho a = b, potom sa rovnosť elipsy pri pohľade nafúkne. Polomer stávky Tsіvnyannya a, A colo - okremy vipadok elіpsa. Elips je možné odoberať z kolíka do polomeru a, stlačiť її dovnútra a/b krát uzdovzh os Ou .
príklad 1. Perevіriti, chi є línia, daná nevedomým sa rovná ![]() , elipsa.
, elipsa.
Riešenie. Vykonávame prepracovanie neslávne známej rіvnyannya. Zastosovuєmoly prevodom voľného člena do pravej časti, člen po členovi vzrástol rovný jednému a rovnakému počtu a rýchlosti zlomkov:

Vidpovid. Otrimane ako výsledok premeny rovných na kanonické rovné elipsy. Otzhe, čiara tsya - elipsy.
zadok 2. Položte kanonické vyrovnanie elipsy, ako keby to bolo rovnakým spôsobom 5 a 4.
Riešenie. Žasneme nad vzorcom kanonickej ekvivalencie elipsy a predstavujeme si: Veľký pivvis - tse a= 5, mensha pіvvіs - tse b= 4. Berieme kanonické vyrovnanie elipsy:
Body ta , označené zelenou farbou na väčšej osi, de
volal triky.
volal výstrednosť elipsa.
Nastavenie b/a charakterizuje „sploštenie“ elipsy. Čo je menej ako vіdnoshennia, tým silnejší je elіps vityagnuty vzdovzh veľká os. Kroky zakrivenia elipsy sa však často premieňajú na excentricitu, ktorej vzorec je navrhnutý vyššie. Pre rôzne elipsy sa excentricita mení z 0 na 1, pričom zostáva menej ako jedna.
príklad 3. Zložte kanonicky rovnakú elipsu, aby ste medzi ohniskami videli drahšie 8 a viac o to krajších 10.
Riešenie. Robimo nemotorný visnovki:
Ak je viac ako polovica drahšia 10, potom її polovica, potom pіvvіs a = 5 ,
Ak vidíte medzi trikmi drahšie 8, tak číslo c zo súradníc ohniska 4.
Nahraďte a vypočítajte:

Výsledkom je kanonické vyrovnanie elipsy:
zadok 4. Položte kanonické vyrovnanie elipsy, ako keby to bolo drahšie 26 a excentricita.
Riešenie. Aká hlasná a veľká je os a rovná sa excentricite, veľký pіvvіs elіps a= 13. Z sa rovná centricite čísla c, je potrebné vypočítať požadovanú sumu peňazí:
![]() .
.
Vypočítajte druhú mocninu menšieho množstva dozhini:

Zložíme kanonické vyrovnanie elipsy:
Príklad 5. Označte ohnisko elipsy danej kanonickou rovnosťou.
Riešenie. Ďalej poznať číslo c, čo označuje prvé súradnice ohniskov elipsy:
![]() .
.
Odstráňte ohnisko elipsy:
![]()
Príklad 6. Zamerajte elіpsa roztashovanі na os Vôl symetricky k klasu súradníc. Zložte kanonické vyrovnanie elipsy takto:
1) stojí medzi ohniskami 30 a veľkými všetkými 34
2) malé je 24 a jedno z ohniskov je v bode (-5; 0)
3) excentricita a jedno z ohniskov je v bode (6; 0)
Pokračujeme v plnení misie na elipsách naraz
Ak je bod elipsy dostatočný (na kresle je označený zelenou farbou v pravej hornej časti elipsy) a dosahuje stred bodu v ohnisku, potom vzorce pre krok sú:
Pre bod pokožky, ktorý by mal ležať na elipse, je súčet počtu ohniskových bodov konštantná hodnota rovnajúca sa 2 a.
Rovný, čo znamená rovný
volal riaditeľov elіpsa (na kresle - červené čiary pozdĺž okrajov).
Z dvoch vishchenovednykh sa rovná vyplyvay, scho pre akýkoľvek bod elipsy
![]() ,
,
de і - odstránenie tsієї bodov do smerovej čiary і.
Príklad 7. Danius elips. Uložte riaditeľky jogy.
Riešenie. Čudujeme sa na úrovni režisérov a vidíme, že je potrebné poznať výstrednosť elipsy, tobto. Použiť údaje pre tsgogo є. Vypočítame:
 .
.
Berieme do úvahy rovnaké adresáre elipsy:
![]()
Príklad 8. Zložte elipsu kanonicky rovnomerne, akoby s ohniskami - bodkami a riaditeľmi - rovnými čiarami.