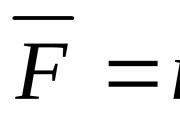RUCH KOKYBĖS TEOREMA (diferencine forma).

1. Taškui: panašiai kaip taškų skaičius per valandą, tas pats galioja ir jėgos taškui:

arba koordinačių forma:

2. Sistemai: jis panašus į sistemos jėgų skaičių per valandą, palyginti su sistemos išorinių jėgų viršūnės vektoriumi (išorinių jėgų, pridėtų prie sistemos, vektorių suma):

arba koordinačių forma:

IMPULSŲ TEOREMA (rankų skaičiaus galinėje formoje teorema).

1. Taškui: taškų skaičiaus keitimas valandos pabaigoje yra lygus jėgos taškui taikomų impulsų sumai (arba vienodo poveikio jėgos taškui impulsui)

arba koordinačių forma:

2. Sistemai: sistemos rankenos dydžio pakeitimas per galutinį valandos intervalą yra lygus išorinių jėgų impulsų sumai:

arba koordinačių forma:

Paveldėjimai: dėl išorinių jėgų sistemos žlugimo dydis yra pastovus; Kadangi išorinės sistemos jėgos yra statmenos giedojimo ašiai, tai rankos tūrio projekcija į visumą yra pastovi reikšmė.

TEOREMA APIE UOLŲ MOMENTĄ

1. Taškui: ji yra panaši į valandą nuo taško rankenos stiprumo momento iki to paties centro (ašies), ta pati momentų suma, taikoma jėgų taškui į tą patį centrą (ašį):

2. Sistemai:

Tai panaši į valandą nuo sistemos galios kiekio momento iki to paties centro (ašios) santykinės sistemos išorinių jėgų momentų sumos iki to paties centro (ašios):

Paveldėjimas: jei sistemos išorinės jėgos neleidžia sukimo momento atiduoti centrui (ašiai), tai sistemos rankenos sukimo momentas centrui (ašiai) yra pastovi reikšmė.

Jei tašką veikianti jėga neleidžia suteikti momento centrui, tai taško rankenos sukimo momentas iki centro yra pastovi reikšmė ir taškas apibūdina plokščią trajektoriją.

TEOREMA APIE KINETINĘ ENERGIJĄ

1. Taškui: taško kinetinės energijos pokytis gale ir prieš jį veikiančių aktyviųjų jėgų poslinkis (prieš aktyviąsias jėgas įtraukiamos papildomos netobulų jungčių sandėlio reakcijos):

Išorinės jėgos taikymui: taško kinetinės energijos pokytis tradiciniam robotui veikiant išoriniam jam veikiančių aktyviųjų jėgų ir nešiojamos inercijos jėgos (skyrius „Privatūs integravimo tipai“):

2. Sistemai: sistemos kinetinės energijos keitimas bet kuriame jai pritaikyto dabartinio roboto poslinkio taške, srovės aktyviosios jėgos ir vidinės jėgos, veikiančios sistemos taškuose, stovėjimas tarp bet kokių pakeitimų yra:

Kadangi sistema yra nekintanti (tvirtas kūnas), tai ΣA i =0 ir kinetinės energijos pokytis tradicinius robotus palieka be išorinių aktyviųjų jėgų.

TEOREMA APIE MECHANINĖS SISTEMOS RUCH CENTRĄ. Mechaninės sistemos masės centras griūva kaip taškas, kurio masė yra visos sistemos masė M = Σm i , kol veikia visos išorinės sistemos jėgos:

arba koordinačių forma:

de - pagreitis iki projekcijos Dekarto koordinačių ašyje stiebo centro; Išorinė jėga yra jos projekcija Dekarto koordinačių ašyse.

IMPULSŲ TEOREMA SISTEMAI, VIRUOTAI PER MASĖS CENTRO VEIKŠĮ.

Sklandumo pokytis masės sistemos centrui per paskutinę valandos laikotarpį yra lygus sistemos išorinių jėgų impulsui per tą patį valandos laikotarpį, padalijus iš visos sistemos masės.

Dinamikos teoremos- Tai teorema apie mechaninės sistemos centro judėjimą, teorema apie rankos stiprumo pasikeitimą, teorema apie rankos galvos sukimo momento pasikeitimą (kinetinį momentą) ir teorema apie pokytį mechaninės sistemos kinetinėje energijoje.

Teorema apie mechaninės sistemos centro judėjimą

Teorema apie roc į masės centrą.
Sistemos masės pridėjimas prie pagreitinto masės centro yra visų sistemą veikiančių išorinių jėgų vektorinė suma:
.

Čia M yra sistemos masė:
;
a C – pagreitintas iki masės sistemos centro:
;
v C - masės sistemos centro sklandumas:
;
r C - spindulio vektorius (koordinatės) iki masės sistemos centro:
;
- koordinuoti (iki nesunaikinamo centro) taškų, iš kurių susidaro sistema, masę.

Teorema apie rankos impulso (impulso) pokytį

Sistemos stiprumas (impulsas)Šiuolaikinis visos sistemos masės tiekimas masės centro sklandumui arba aplinkinių taškų ar dalių srautų skaičiaus sumai (impulsų sumai), kad būtų sukurta sistema:
.

Teorema apie rankų skaičiaus kitimą diferencine forma.
Valanda po valandos sistemos įtakos (impulso) dydis yra tradicinė visų sistemą veikiančių išorinių jėgų vektorinė suma:
.

Teorema apie rankų skaičiaus keitimą integralioje formoje.
Sistemos galios (impulso) dydžio keitimas tam tikrą laikotarpį yra lygus išorinių jėgų impulsų dydžiui per tą patį laikotarpį:
.

Impulso (impulso) energijos taupymo dėsnis.
Kadangi visų sistemą veikiančių išorinių jėgų suma lygi nuliui, tai sistemos įtakos vektorius bus pastovus. Tada visos koordinačių ašių projekcijos laikomos pastoviomis vertėmis.

Kadangi visų išorinių jėgų projekcijų suma lygi nuliui, tai didelės sistemos dalies projekcija bus stabili.

Teorema apie galvos momento pasikeitimą į ranką (momento teorema)

Pagrindinis sistemos sukimosi į tam tikrą centrą O dydžio momentas yra vertė, lygi visų sistemos taškų sukimosi į centrą momentų vektorinei sumai:
.
Čia kvadratinės rankos reiškia vektorių tir.

Tvirtinamos sistemos

Ši teorema taikoma taškui, kuriame mechaninė sistema yra prijungta prie nenutrūkstamo taško arba su visu tašku, kuris ateityje bus pritvirtintas prie inercinės sistemos. Pavyzdžiui, korpusas tvirtinamas sferiniu guoliu. Arba kūnų sistema, kuri sukuria griūtį aplink nesunaikinamą centrą. Apvyniotas visas kūnas arba kūno sistema taip pat gali būti nepažeista. Šiuo atveju pagal momento momentus suprantami impulso momentai ir fiksuotos ašies jėgos.

Teorema apie galvos momento pasikeitimą į ranką (momento teorema)
Tai tarsi valanda nuo sistemos visumos galvos momento iki to paties nesunaikinamo centro apie senovės visų išorinių sistemos jėgų momentų sumą iki to paties centro.

Pagrindinio impulso momento (impulso momento) išliekamumo dėsnis.
Kadangi visų taikymų išorinių jėgų sistemai momentų suma į šį nesunaikinamą centrą O yra lygi nuliui, tai pagrindinis sistemos momentas bus stabilus. Tada visos koordinačių ašių projekcijos laikomos pastoviomis vertėmis.

Kadangi išorinių jėgų momentų išilgai bet kurios nepajudinamos ašies suma yra lygi nuliui, sistemos sukimosi išilgai šios ašies momentas bus pastovus.

Papildomos sistemos

Dabar teorema turi universalų pobūdį. Vaughn yra sustingęs tiek fiksuotų sistemų, tiek rimtai griūvančių sistemų atžvilgiu. Esant tvirtinimo sistemoms, užtikrinama raiščių reakcija tvirtinimo taškuose. Tai išplaukia iš ankstesnės teoremos, fiksuotąjį tašką O pakeičiant masės sistemos C centru.

Momentų teorema į masės centrą
Ji panaši į valandą nuo sistemos judėjimo dydžio galvos momento iki senosios visų išorinių sistemos jėgų momentų sumos masės C centro iki to paties centro.

Momento ir impulso likimo dėsnis.
Jei visų išorinių jėgų sistemos momentų suma iki masės centro C yra lygi nuliui, tai visos sistemos galvos momentas į centrą bus pastovus. Tada visos koordinačių ašių projekcijos laikomos pastoviomis vertėmis.

Kūno inercijos momentas

Kai kūnas apsivynioja aplink z ašį Esant ašiniam sklandumui ω z, tada rankos sukimosi momentas (kinetinis momentas) išilgai z ašies apskaičiuojamas pagal formulę:
L z = J z ω z ,
čia J z – kūno inercijos momentas išilgai z ašies.

Kūno inercijos momentas išilgai z ašies nurodyta pagal formulę:
,
kur h k – stovėti nuo taško, kurio masė m k, iki z ašies.
Plonas žiedas, kurio masė M ir spindulys R arba cilindras, kurio masė pasiskirsto už jo ratlankio,
J z = MR 2 .
Vieno vienodo žiedo ar cilindro atveju
.

Steinerio-Huygenso teorema.
Tegul Cz – viskas, kas eina per kūno centrą, Oz – viskas, kas jam lygiagreti. Šie kūno inercijos momentai yra susiję su šiomis ašimis:
J Oz = J Cz + M a 2 ,
de M – kūno masė; a – stovėti tarp ašių.

Beprotišku būdu:
,
de – kūno inercijos tenzorius.
Čia yra vektorius, brėžiamas iš kūno masės centro taške už masės m k.

Teorema apie kinetinės energijos kitimą

Tegul masės M kūnas suformuoja progresyvią ir vertikalią rukę su storu takumu priekinėje ašyje z. Todėl kūno kinetinė energija apskaičiuojama pagal šią formulę:
,
de v C – takumas kūno centre;
J Cz – kūno inercijos momentas išilgai ašies, einančios per kūno centrą lygiagrečiai vyniojimo ašiai. Tiesiogiai įvyniojimo ašys laikui bėgant gali keistis. Pateikta formulė pateikia kinetinės energijos mittev reikšmę.

Teorema apie sistemos kinetinės energijos kitimą diferencine forma.
Sistemos kinetinės energijos skirtumas (padidėjimas) faktiškai pasislinkus papildomiems darbo diferencialų kiekiams, dėl kurių visos programos perkeliamos į išorinių ir vidinių jėgų sistemą:
.

Teorema apie sistemos kinetinės energijos kitimą integralioje formoje.
Sistemos kinetinės energijos pokytis faktinio vidinių sumų poslinkio metu veikia visų išorinių ir vidinių jėgų sistemos įėjimų poslinkį:
.

Darbas, kuris yra veiksmo galia, kuris panašus į jėgos vektorių skaliarinį sudėjimą ir be galo mažą taško poslinkį:
,
vektoriaus F ir ds modulius pridėti prie vektoriaus tarp jų kosinuso.

Darbas, kuris yra galios momentas, panašus į vektorių skaliarinį pridėjimą momento ir be galo mažo sukimosi metu:
.

d'Alemberto principas

D'Alembert principo esmė yra originalią dinamiką perkelti į pradinę statiką. Dėl šios priežasties daroma prielaida (arba žinoma iš anksto), kad sistemos kūnai gali pradėti greitėti. Toliau įveskite inercijos jėgas ir (arba) inercijos jėgų momentus, kurie yra lygūs tiesioginių jėgų ir jėgų momentų dydžiui ir sukimuisi, kurie pagal mechanikos dėsnius sukuria pagreičio arba pagreičio ribinio pagreičio uždavinius.

Pažvelkime į užpakalį. Kūne vyksta progresyvus judėjimas ir išorinės jėgos veikia naują. Be to, darome prielaidą, kad bandome sukurti pagreitį iki masės sistemos centro. Pagal teoremą apie kūno centro judėjimą pagreitinamas ir kūno kūno centras, tarsi kūnas veiktų jėga. Toliau naudojame inercijos jėgą:
.
Pagal šiuos dinamikos duomenis:
.
;
.

Bendrajam rukh turi būti laikomasi panašios tvarkos. Tegul kūnas apsisuka apie z ašį ir naujas jėgos momentas M e zk. Manome, kad šie momentai sukuria kritinį pagreitį z. Toliau pristatome inercijos jėgų momentą M І = - J z z . Pagal šiuos dinamikos duomenis:
.
Paverčiama originalia statika:
;
.

Galimybės judėti principas

Galimų judesių principas grindžiamas aukščiausia statika. Tam tikroms užduotims jis suteikia trumpesnį sprendimą, žemesnį išlyginimo lygį. Ypač svarbios sistemos su jungtimis (pavyzdžiui, kūno sistemos, sujungtos siūlais ir blokais), kurios susidaro dėl kūnų beasmeniškumo.

Galimybės judėti principas.
Sklandžiai mechaninei sistemai su idealiais ryšiais būtina ir pakanka, kad visų ją veikiančių aktyviųjų jėgų elementaraus darbo suma, esant bet kokiam galimam sistemos poslinkiui, pasiektų nulį.

Galimybė perkelti sistemą- reikia tik nedidelio judesio, kad nebūtų sunaikinti raiščiai ir ant jų esanti sistema.

Idealios jungtys– tokias jungtis atlieka robotai, judindami sistemą. Tiksliau, darbo kiekis, kuris atsiranda tarp pačių jungčių, kai sistema perkeliama, yra lygus nuliui.

Išorinė dinamika (D'Alembert-Lagrange principas)

D'Alembert-Lagrange principas yra D'Alembert principo ir galimų judesių principo derinys. Tada, kai dinamikos užduotis atsiejama, įvedame inercines jėgas ir sumažiname duotas jėgas iki duotosios statikos, kuri remiasi papildomu galimų poslinkių principu.

D'Alembert-Lagrange principas.
Rusijos mechaninėje sistemoje su idealiomis jungtimis bet kuriuo momentu visų aktyviųjų jėgų ir visų inercinių jėgų elementariųjų operacijų suma bet kurioje galimai pasislinkusioje sistemoje yra lygi nuliui:
.
Ceremonija vadinama iki ekstremalių dinamikos lygių.

Lagrange's Rivne

Ušagalny koordinatės q 1 , q 2 , ..., q n - tai n dydžių rinkinys, kuris vienareikšmiškai nurodo sistemos padėtį.

Koordinačių skaičius n didėja didėjant sistemos laisvės laipsnių skaičiui.

Sureguliuotos kainos- tai maršrutas iš koordinačių už valandos t.

Įprastos jėgos Q 1 , Q 2 , ..., Q n .
Pažiūrėkime į galimą sistemos poslinkį, kurioje koordinatė q k atima poslinkį δq k. Kitos koordinatės nebėra nepakitusios. Tegul δA k yra robotas, kurį tokio poslinkio metu veikia išorinės jėgos. Todi
δA k = Q k δq k , arba
.

Kadangi judant sistema pasikeičia visos koordinatės, tai robotas, kurį tokio judėjimo metu veikia išorinės jėgos, atrodo taip:
δA = Q 1 δq 1 + Q 2 δq 2 + ... + Q n δq n.
Tada yra formalios jėgos ir privatūs judėjimo panašumai:
.

Dėl potencialių jėgų su potencialu Π,
.

Lagrange's Rivne- mechaninės sistemos derinimas koordinatėmis:

Čia T yra kinetinė energija. Vaughn yra koordinačių, greičių ir, galbūt, valandos funkcija. Todėl jis taip pat turi privačią funkciją, pvz., paslėptas koordinates, greitį ir laiką. Tada būtina užtikrinti, kad laikrodžio koordinatės ir greitis veiktų. Todėl, norint rasti nuoseklią analogiją su laiku, būtina nustatyti lankstymo funkcijos diferenciacijos taisyklę:
.

Wikorystan literatūra:
S. M. Targ, Trumpas teorinės mechanikos kursas, „Vishcha mokykla“, 2010 m.

(MECHANINĖS SISTEMOS) - IV variantas

1. Pagrindinė materialaus taško dinamikos lygybė, matyt, išreiškiama lygybėmis. Skirtingi poveikio lygiai tam tikruose nepastovios mechaninės sistemos taškuose, pagrįsti dviejų tipų jėgomis, gali būti parašyti dviem formomis:

(1) , kur k = 1, 2, 3, ..., n - materialios sistemos taškų skaičius.

de - k-ojo taško masė; - k-taško spindulio vektorius, - duotoji (aktyvioji) jėga, veikianti k-tašką arba visų aktyviųjų jėgų, veikiančių k-tašką, balansas. - vienoda raiščių reakcijos jėga, kuri veikia k-ąjį tašką; - lygi vidinėms jėgoms, veikiančioms k-ąjį tašką; - lygus išorinėms jėgoms, veikiančioms k-ąjį tašką.

Koregavimų (1) ir (2) pagalba galite reguliuoti ir pirmąją, ir kitą dinamiką. Išspręsti kitą sistemos dinamikos rinkinį yra gana sudėtinga matematiniu požiūriu, tačiau vis tiek susiduriame su dideliais sunkumais. Smirda tame, kad tiek sistemose (1), tiek sistemose (2) lygių skaičius yra žymiai mažesnis nei nežinomų.

Taigi, jei (1) yra teisingas, tada dinamika bus matoma kitai (grįžimo) dinamikai ir , o dinamika bus nematoma . Vektorių lygiai bus " n“, o nematomi – „2n“.

Kai tik išeiname iš rangų sistemos (2), tada išeina dalis išorinių jėgų. Kodėl dalis? Dešinėje yra tai, kad prieš patenkant išorinėms jėgoms ir išorinės raiščių reakcijos nežinomos. Iki tol jie liks nematomi.

Taigi, kadangi sistema (1) ir sistema (2) yra UŽDARYTA. Būtina pridėti raiščių išlyginimą, išlyginimą ir išlyginimą, o galbūt ir patiems raiščiams reikia uždėti briaunas. Kas tai nedrąsu?

Kaip ir (1), galite sekti Lagranžo pirmos rūšies upių keliu. Jei toks kelias nėra racionalus tam, kas paprastesnė už užduotį (mažiau laisvės žingsnių), matematikos akimis svarbiau jį reitinguoti.

Tada aš labai gerbiu sistemą (2), amžinai nežinomą. Pirmą kartą paleidus sistemą, reikia ją išjungti, kad nesimatytų. Svarbu pažymėti, kad mūsų, kaip taisyklė, neįtakoja vidinės Rusijos sistemos jėgos, todėl sistemai griūvus nebūtina žinoti, kaip griūva kiekvienas sistemos taškas, o užtenka. žinoti, kaip žlunga visa sistema.

Taip pat, jei sistemą išjungiame skirtingais būdais (2) su nematomomis jėgomis, galime pašalinti jungties veiksmus, t.y., yra tam tikros paslėptos sistemos savybės, kurių žinojimas leidžia spręsti, kaip sistema griūva. Šios charakteristikos įvedamos papildomiems rangams dinamikos teoremos. Tokios chotiri teoremos:

1. Teorema apie rukh centre mas mechaninė sistema;

2. Teorema apie Keičiamos kelios mechaninės sistemos dalys;

3. Teorema apie keičiant mechaninės sistemos kinetinį momentą;

4. Teorema apie mechaninės sistemos kinetinės energijos pokyčiai.

Rusijos Federacijos švietimo ir mokslo ministerija

Federalinis valstybės biudžetinis švietimas aukštajam profesiniam išsilavinimui įgyti

"Kubanos valstybinis technologijos universitetas"

Teorinė mechanika

2 dalies dinamika

Patvirtino Redakcija

Džiaugiuosi universitete

pradinis pagalbininkas

Krasnodaras

UDC 531.1/3 (075)

Teorinė mechanika. 2 dalis. Dinamika: pagrindinis vadovas/L.I. Draiko; Kubanas. laikantis technol.un-t. Krasnodaras, 2011. 123 p.

ISBN 5-230-06865-5

Teorinė medžiaga pateikiama trumpai, taikant naujausias instrukcijas, kurių dauguma atspindi realią mitybos įrangą, gerbiamas racionalaus mitybos būdo pasirinkimas.

Skirta kasdienio gyvenimo, transporto ir mašinų gamybos maršrutų korespondencijos ir nuotolinio mokymosi bakalaurams.

Lentelė 1 Ill. 68 Bibliogr. 20 pavadinimų

Mokslinis redaktorius Ph.D. tech. Mokslai, docentas V.F.Melnikovas

Recenzentas: galva. Kubano agrarinio universiteto Teorinės mechanikos ir Mechanizmų bei mašinų teorijos katedra prof. F.M. Kanariovas; Kubano valstybinio technologijos universiteto Teorinės mechanikos katedros docentas M.I. Keli

Palaiko redakcinius sprendimus Kubano valstybinio technologijos universiteto labui.

Iki pasimatymo

ISBN 5-230-06865-5 KubDTU 1998 rub.

Peredmova

Tai pradinis užduočių vadovas ištęstinių studijų studentams studijuoti buities, transporto ir mechanikos inžinerijos specialybes, o galbūt ir prašymams pildyti teorinės mechanikos kurso skyrių „Dinamika“ kitų specialybių ištęstinių studijų studentams, kaip taip pat nuolatinių studijų studentams, dalyvaujantiems savarankiškame darbe.

Vadovėlis sudarytas pagal pagrindinę teorinės mechanikos kurso programą, kurioje pateikiama visa mityba pagrindinei kurso daliai. Kozhen pasidalino trumpa teorine medžiaga su iliustracijomis ir metodinėmis rekomendacijomis jūsų karjerai atliekant aukšto lygio užduotis. Darbuotojas turi 30 užduočių sprendimą, kuris atspindi realų įrangos tiekimą ir panašias valdymo užduotis savarankiškam vystymuisi. Odos problemos atveju pateikiama suskirstymo schema, kuri aiškiai iliustruoja sprendimą. Sprendimo įforminimas užtikrina galimybę atlikti ištęstinių studijų studentų kontrolinį darbą.

Autorius labai dėkoja Kubos agrarinio universiteto Teorinės mechanikos ir Mechanizmų ir mašinų teorijos katedrai už puikų darbą peržiūrint pradinį vadovėlį, taip pat Kubos teorinės mechanikos katedros indėlį. Valstybinis technologas Sveikiname universitetą už vertingą pagarbą ir gerą pradinio studento pasirengimą prieš jį matant.

Autorius atitinkamai priims visas kritines pastabas ir svarstymus.

Įeikite

Dinamika yra svarbiausia teorinės mechanikos šaka. Dauguma specifinių užduočių, tenkančių inžinerinei praktikai, turi išlikti dinamiškos. Vikoristo statikos ir kinematikos, dinamikos principai nustato paslėptus materialių kūnų tėkmės dėsnius, veikiant jėgoms.

Paprasčiausias materialus objektas yra materialus taškas. Bet kokios formos ar dydžio materialus kūnas gali būti laikomas nagrinėjamos problemos materialiu tašku. Galinių matmenų korpusas gali būti laikomas materialiu tašku, nes šio taško svarba Rusijoje šiai užduočiai netinka. Taip atsitinka, kai kūno dydis yra mažas ir lygus atstumams, per kuriuos eina kūno taškai. Kieto kūno odos dalis prispaudžiama materialiu tašku.

Jėga, veikiama materialaus kūno taške, progresyvi dinamika vertinama iš jo dinaminio įtekėjimo, t.y., pagal tai, kaip keičiasi materialių objektų srauto charakteristikos.

Dainavimo sistemos platybėse pamažu atsiranda materialių objektų srautas. Klasikinėje mechanikoje, kuri remiasi Niutono aksiomomis, erdvė laikoma trivialia, jos galia neslysta už materialių objektų, kurie griūva naujame. Taško padėtis tokioje erdvėje nurodoma trimis koordinatėmis. Valanda siejama su erdve ir materialių objektų tėkme. Tačiau jį gerbia visos gyvenimo sistemos.

Dinamikos dėsniai apibūdina materialių objektų tėkmę išilgai absoliučių koordinačių ašių, kurios mintyse priimamos kaip nestruktūros. Absoliučios koordinačių sistemos pradžia imama Saulės centre, o ašys yra tiesios per atstumą, veidrodžiai nėra psichiškai trapūs. Turint tiek daug techninių išteklių, nėra lengva suprasti Žemės koordinačių ašis.

Medžiagų objektų mechaninio judėjimo laipsniškoje dinamikoje parametrai nustatomi matematiniais skaičiavimais iš pagrindinių klasikinės mechanikos dėsnių.

Pirmasis dėsnis (inercijos dėsnis):

Materialus taškas išsaugo ramaus arba tolygaus ir tiesaus judėjimo būseną tol, kol jokia jėga jo nepašalina iš būsenos.

Tolygus ir tiesus taško judėjimas vadinamas inercijos judėjimu. Ramiai, impulso kritimą uždarysime už inercijos, jei taško sklandumas lygus nuliui.

Nesvarbu, koks materialus taškas yra inertiškas, ramaus ar tolygaus, tiesaus judėjimo būsenos išsaugoti neįmanoma. Sistema, kuri yra griežtai valdoma inercijos dėsnio, vadinama inercija, o revoliucija, kuri visiškai atitinka sistemą, vadinama absoliučia. Bet kuri sistema, veikianti inercinės sistemos atžvilgiu, turės linijinį ir tolygų judėjimą, kuris taip pat bus inercinė sistema.

Kitas dėsnis (pagrindinis dinamikos dėsnis):

Materialaus taško pagreitis į inercinę sistemą atsiranda dėl proporcingos jėgos pridėjimo prie taško ir yra veikiamas jėgos už tiesioginės linijos:
.

Pagal pagrindinį dinamikos dėsnį parodo, kokios jėgos
tvirtinimas
. Taško masė apibūdina pokyčio taško atramos lygį ir sklandumą, tai yra materialaus taško inercijos laipsnį.

Trečiasis dėsnis (veiksmo ir prieštaravimo įstatymas):

Jėgos, dėl kurių du kūnai veikia vienas kitą, yra vienodos už modulio ir tiesios išilgai vienos pusės priešinga kryptimi.

Jėgos, vadinamos procesu ir reakcija, taikomos skirtingiems kūnams, todėl ta pati sistema neveikia.

Ketvirtasis įstatymas (pajėgų nepriklausomybės įstatymas):

Vieną valandą veikiant daugybei jėgų, materialaus taško pagreitis yra lygus geometrinei pagreičio sumai, tarsi taškas būtų pagreitintas veikiant odos jėgai:

, de
,
,…,
.

Vikoristannaya OZMS pagal užduoties kilimo valandą yra susijusi su dainavimo sunkumais. Todėl būtina nustatyti papildomus ryšius tarp srauto charakteristikų ir jėgų, naudingų praktiniam sąstingiui. Su tokiais santykiais išplėstinės dinamikos teoremos. Jie, būdami OMS paveldėtojais, nustato skirtumus tarp tam tikrų specialiai įvestų Rusijos Federacijos požiūrių kaitos greičio ir išorinių jėgų savybių.

Teorema apie rankos stiprumo kitimą. Įveskime materialaus taško rankos stiprumo vektoriaus (R. Dekarto) sampratą (3.4 pav.):

I i = t V G (3.9)

Mažas 3.4.

Sistemai pristatome koncepciją sistemos galvos vektorius kaip geometrinė suma:

Q = Y, m "V r

Pagal sveikatos draudimą: Hyu, -^=ya) arba X

R(E).

Siekiant užtikrinti, kad /w, = const būtų praleistas: -Ym,! R (E) ,

arba likusioje išvaizdoje

dO/di = A (E (3.11)

tobto. Pirmasis yra panašus į galvos vektoriaus valandą, kiek sistema yra senesnė už išorinių jėgų galvos vektorių.

Teorema apie roc į masės centrą. Masinės sistemos centras Pavadinkite geometrinį tašką, kurio padėtis yra T, i. masės dalyboje /g/, sistemoje ji rodoma spindulio vektoriumi iki masės centro (3.5 pav.):

de g z - spindulio vektorius iki masės centro.

Mažas 3.5.

Būtent = t nuo sistemos masės. Padauginus virusą

nya (3.12) ant reklamjuostės ir abiejų napiv- dalių diferenciacijos

Vertinga lygybė atsiranda dėl: g s t s = ^t.u. = 0 arba 0 = t z U s.

Tokiu būdu pagrindinis sistemos galios vektorius yra toks pat kaip masės tiekimas sistemai ir sklandumas masės centrui. Vikoristo teorema apie rankų skaičiaus pokytį (3.11) atmetama:

t z dU z / dі = A (E), arba

Formulė (3.13) apibrėžia masės centro judėjimo teoremą: masių sistemos centras griūva kaip materialus taškas, kuris neša sistemos masę, veikdamas kaip išorinių jėgų galvos vektorius.

Teorema apie judrumo momento kitimą. Įveskime materialaus taško dydžio momento, kaip vektoriaus pridėjimo prie spindulio vektoriaus ir rankenos dydžio, sampratą:

iki oi = bl X kad, (3.14)

de į OI - stiprumo momentas tarp materialaus taško ir nesunaikinamo taško Apie(3.6 pav.).

Dabar svarbus yra mechaninės sistemos stiprumo momentas kaip geometrinė suma:

К() = X ko, = ШУ, ? O-15>

Diferencijavimas (3.15) atmetamas:

Ґ sek--- X t i U. + g u X t i

Vrahovoyuchi scho = U G U i X t i u i= 0, tada formulę (3.2) galima pašalinti:

сіК а /с1ї - ї 0 .

Pakeitus kita išraiška (3.6), mums liks teorema apie sistemos stiprumo momento pokytį:

Pirmasis panašus į mechaninės sistemos žlugimo momentą, panašus į nesunaikinamą centrą, panašus į išorinių jėgų, veikiančių šią sistemą, galvos momentą, panašus į tą patį centrą.

Kai buvo parodytas santykis (3,16), buvo perteikta, kad Apie– Esmė nepalaužiama. Tačiau galima parodyti, kad kitais atvejais santykių tipas (3.16) nesikeičia, nors plokščiosios Rusijos atveju momentinis pasirinkimo taškas yra masės centre, sklandumo ar pagreičio centre. Krymas, tai esmė Apie bėga nuo materialaus taško, kuris žlunga, uolumas (3.16), parašytas, kad šis taškas virstų tuo pačiu kaip 0 = 0.

Teorema apie kinetinės energijos kitimą. Žlugus mechaninei sistemai, keičiasi ir „išorinė“, ir vidinė sistemos energija. Kadangi vidinių jėgų charakteristikos, galvos vektorius ir galvos momentas, nenurodomos kuo greičiau keičiant galvos vektorių ir galvos momentą, tada Prieš vertinant energetikos sistemos procesus, gali įeiti vidinės jėgos. Todėl stebint sistemos energijos pokyčius, matosi šalia esančių taškų griūtis, į kuriuos taip pat taikomos vidinės jėgos.

Materialaus taško kinetinė energija apibrėžiama kaip dydis

T^tuTsg. (3.17)

Mechaninės sistemos kinetinė energija yra senoji sistemos materialių taškų kinetinės energijos suma:

Gerbiamas scho T > 0.

Svarbus yra jėgos intensyvumas, nes jėgos vektoriaus skaliarinis pridėjimas prie greičio vektoriaus: