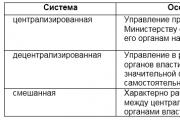
Нескінченно великі та їхні властивості. Визначення нескінченно великої послідовності

30.07.2020

Обчислення нескінченно малих та великих

Обчислення нескінченно малих- обчислення, вироблені з нескінченно малими величинами, у яких похідний результат сприймається як нескінченна сума нескінченно малих. Обчислення нескінченно малих величин є загальним поняттямдля диференціальних та інтегральних обчислень, що становлять основу сучасної вищої математики. Поняття нескінченно малої величини тісно пов'язане з поняттям межі.

Нескінченно мала

Послідовність a nназивається нескінченно малоюякщо . Наприклад, послідовність чисел – нескінченно мала.

Функція називається нескінченно малої на околиці точки x 0 , якщо .

Функція називається нескінченно малої на нескінченності, якщо або .

Також нескінченно малою є функція, що є різницею функції та її межі, тобто якщо , то f(x) − a = α( x) , .

Нескінченно велика величина

Послідовність a nназивається нескінченно великий, якщо .

Функція називається нескінченно великий на околиці точки x 0 , якщо .

Функція називається нескінченно великий на нескінченності, якщо або .

У всіх випадках нескінченність праворуч від рівності мається на увазі певний знак (або «плюс», або «мінус»). Тобто, наприклад, функція x sin xне є нескінченно великою при .

Властивості нескінченно малих і нескінченно великих

Порівняння нескінченно малих величин

Як порівнювати нескінченно малі величини?
Ставлення нескінченно малих величин утворює так звану невизначеність.

Визначення

Припустимо, у нас є нескінченно малі при тому самому величині α( x) та β( x) (або, що не має значення для визначення, нескінченно малі послідовності).

Для обчислення таких меж зручно використовувати правило Лопіталя.

Приклади порівняння

З використанням Про-Символіки отримані результати можуть бути записані в наступному вигляді x 5 = o(x 3). В даному випадку справедливі записи 2x 2 + 6x = O(x) і x = O(2x 2 + 6x).

Еквівалентні величини

Визначення

Якщо , то нескінченно малі величини α та β називаються еквівалентними ().
Очевидно, що еквівалентні величини є окремим випадком нескінченно малих величин одного порядку малості.

При справедливі такі співвідношення еквівалентності: , , .

Теорема

Межа приватного (відносини) двох нескінченно малих величин не зміниться, якщо одну з них (або обидві) замінити еквівалентною величиною.

Ця теорема має прикладне значення при знаходженні меж (див. приклад).

Приклад використання

Замінюючи sin 2x еквівалентною величиною 2 x, отримуємо

Історичний нарис

Поняття "нескінченно мале" обговорювалося ще в античні часи у зв'язку з концепцією неподільних атомів, проте в класичну математику не увійшло. Знову воно відродилося з появою в XVI столітті «методу неподільних» - розбиття досліджуваної фігури на малі перерізи.

У XVII столітті відбулася алгебраїзація числення нескінченно малих. Вони стали визначатися як числові величини, які менші за всяку кінцеву (ненульову) величину і все ж таки не рівні нулю. Мистецтво аналізу полягало у складанні співвідношення, що містить нескінченно малі (диференціали), та був - у його інтегруванні .

Математики старої школи піддали концепцію нескінченно малихрізкої критики. Мішель Ролль писав, що нове числення є « набір геніальних помилок»; Вольтер отруйно зауважив, що це обчислення є мистецтвом обчислювати і точно вимірювати речі, існування яких не може бути доведено. Навіть Гюйгенс зізнавався, що розуміє сенсу диференціалів вищих порядків.

Як іронію долі можна розглядати появу в середині століття нестандартного аналізу, який довів, що первісна точка зору – актуальні нескінченно малі – також несуперечлива і могла б бути покладена в основу аналізу.

Див. також

Wikimedia Foundation. 2010 .

Дивитися що таке "Нескінченно велика" в інших словниках:

Змінна величина Y, обернена до нескінченно малої величини X, тобто Y = 1/X … Великий Енциклопедичний словник

Змінна величина y, обернена до нескінченно малої величини x, тобто y = 1/x. * * * БЕЗКОШТОВНО ВЕЛИКА БЕЗКОНЕЧНО ВЕЛИКА, змінна величина Y, зворотна нескінченно малій величині X, тобто Y = 1/X … Енциклопедичний словник

В математиці, змінна величина, яка в даному процесі зміни стає і залишається абсолютною величиною більше будь-якого наперед заданого числа. Вивчення Би. б. величин може бути зведено до вивчення нескінченно малих. Велика Радянська Енциклопедія

Опр.:Функція називається нескінченно малоюпри , якщо .

У записі « » будемо припускати, що x 0може приймати як кінцеве значення: x 0= Сonst, так і нескінченне: x 0= ∞.

Властивості нескінченно малих функцій:

1) Алгебраїчна сума кінцевого числа нескінченно малих за функцій є нескінченно малою за функцією.

2) Добуток кінцевого числа нескінченно малих за функцій є нескінченно малою за функцією.

3) Добуток обмеженої функції на нескінченно малу функцію є нескінченно малою функцією.

4) Приватне від розподілу нескінченно малої при функції на функцію, межа якої відмінна від нуля, є нескінченно малою при функцією.

приклад: Функція y = 2 + xє нескінченно малою при , т.к. .

Опр.:Функція називається нескінченно великийпри , якщо .

Властивості нескінченно великих функцій:

1) Сума нескінченно великих за функцій є нескінченно великою за функцією.

2) Твір нескінченно великий при функції на функцію, межа якої відмінна від нуля, є нескінченно великою при функцією.

3) Сума нескінченно великий за функції та обмеженої функції є нескінченно великою функцією.

4) Приватне від розподілу нескінченно великий при функції на функцію, що має кінцеву межу, є нескінченно великою за функції.

приклад: Функція y= є нескінченно великий при , т.к. .

Теорема.Зв'язок між нескінченно малими та нескінченно великими величинами. Якщо функція є нескінченно малою при , то функція є нескінченно великою при . І навпаки, якщо функція є нескінченно великою при , то функція є нескінченно малою при .

Відношення двох нескінченно малих прийнято позначати символом, двох нескінченно великих - символом. Обидва відносини є невизначеними тому сенсі, що й межа може як існувати, і існувати, дорівнювати певному числу чи бути нескінченним залежно від виду конкретних функцій, які входять у невизначені висловлювання.

Крім невизначеностей виду та невизначеними є такі вирази:

Різниця нескінченно більших за один знак;

Твір нескінченно малої на нескінченно велику;

Показово-ступенева функція, основа якої прагне 1, а показник – до ;

Показово-ступінчаста функція, основа якої є нескінченно малою, а показник – нескінченно великий;

Показово-статечна функція, основа та показник якої є нескінченно малими;

Показово-статечна функція, основа якої є нескінченно великою, а показник – нескінченно малою.

Говорять, що має місце невизначеність відповідного виду. Обчислення межі називають у цих випадках розкриттям невизначеності. Для розкриття невизначеності вираз, що стоїть під знаком межі, перетворюють на вигляд, що не містить невизначеності.

При обчисленні меж використовують властивості меж, і навіть властивості нескінченно малих і нескінченно великих функцій.

Розглянемо приклади обчислень різних меж.

1) . 2) .

4) , т.к. добуток нескінченно малої функції при обмеженій функції є нескінченно малою.

5) . 6) .

7) = =

. В даному випадку мала місце невизначеність типу, яку вдалося розкрити за допомогою розкладання багаточленів на множники та скорочення на загальний множник.

= .

В даному випадку мала місце невизначеність типу , яку вдалося розкрити за допомогою множення чисельника і знаменника на вираз , використання формули і подальшого скорочення дробу на ( +1).

9)
. В даному прикладі невизначеність типу була розкрита почленним розподілом чисельника та знаменника дробу на старший ступінь.

Чудові межі

Перша чудова межа : .

Доведення.Розглянемо одиничне коло (рис.3).

Рис.3. Одиничне коло

Нехай х– радіальний захід центрального кута МОА(), тоді ОА = R= 1, МК= sin x, AT= tg x. Порівнюючи площі трикутників ОМА, ОТАта сектора ОМА, Отримаємо:

Розділимо останню нерівність на sin x, Отримаємо:

Так як при , то за якістю 5) меж

Звідки і обернена величина при тому, що й потрібно було довести.

Примітка:Якщо функція є дуже малою при , тобто. , то перша чудова межа має вигляд:

Розглянемо приклади обчислень меж з використанням першої чудової межі.

При обчисленні цієї межі використовували тригонометричну формулу: .

Розглянемо приклади обчислень меж з використанням другої чудової межі.

2) .

3) . Має місце невизначеність типу. Зробимо заміну, тоді; при .

Функція y=f(x)називається нескінченно малоюпри x→aабо при x→∞, якщо або , тобто. нескінченно мала функція – це функція, межа якої у цій точці дорівнює нулю.

приклади.

1. Функція f(x)=(x-1) 2 є нескінченно малою при x→1, оскільки (див. мал.).

2. Функція f(x)= tg x- нескінченно мала при x→0.

3. f(x)= ln (1+ x) - нескінченно мала при x→0.

4. f(x) = 1/x- нескінченно мала при x→∞.

Встановимо наступне важливе співвідношення:

Теорема.Якщо функція y=f(x)представима при x→aу вигляді суми постійного числа bта нескінченно малої величини α(x): f(x)=b+ α(x)те.

Назад, якщо , то f(x)=b+α(x), де a(x)- нескінченно мала при x→a.

Доведення.

1. Доведемо першу частину затвердження. З рівності f(x)=b+α(x)слід | f (x) - b | = | α|. Але так як a(x)– нескінченно мала, то при довільному ε знайдеться δ – околиця точки a,при всіх xз якої значення a(x)задовольняють співвідношення |α(x)|< ε. Тоді |f(x) – b|< ε. А це означає, що .

2. Якщо , то за будь-якого ε >0 для всіх хз деякої δ – околиця точки aбуде |f(x) – b|< ε. Але якщо позначимо f(x) - b = α, то |α(x)|< ε, а це означає, що a– нескінченно мала.

Розглянемо основні властивості нескінченно малих функцій.

Теорема 1.Алгебраїчна сума двох, трьох і взагалі будь-якого кінцевого числа нескінченно малих є функція нескінченно мала.

Доведення. Наведемо доказ для двох доданків. Нехай f(x)=α(x)+β(x), де і . Нам потрібно довести, що при довільному як завгодно малому? > 0 знайдеться δ> 0, таке, що для x, які задовольняють нерівності | x – a |<δ , виконується |f(x)|< ε.

Отже, зафіксуємо довільне число ε > 0. Оскільки за умовою теореми α(x)- нескінченно мала функція, то знайдеться таке? > 0, що за | x – a |< δ 1 маємо |α(x)|< ε / 2. Аналогічно, оскільки β(x)- нескінченно мала, то знайдеться таке δ 2 > 0, що за | x – a |< δ 2 маємо | β(x)|< ε / 2.

Візьмемо δ=min(δ 1 , δ 2 } . Тоді на околиці точки aрадіусу δ виконуватиметься кожна з нерівностей |α(x)|< ε / 2 та | β(x)|< ε / 2. Отже, в цій околиці буде

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,

тобто. |f(x)|< ε, що потрібно було довести.

Теорема 2.Добуток нескінченно малої функції a(x)на обмежену функцію f(x)при x→a(або при x→∞) є нескінченно мала функція.

Доведення. Оскільки функція f(x)обмежена, то існує кількість Мтаке, що за всіх значень xз деякої околиці точки a|f(x)|≤M.Крім того, оскільки a(x)- нескінченно мала функція при x→a, то для довільного ε > 0 знайдеться околиця точки a, в якій виконуватиметься нерівність |α(x)|< ε /M. Тоді в меншому з цих околиць маємо | αf|< ε /M= ε. А це означає, що af– нескінченно мала. Для випадку x→∞Доказ проводиться аналогічно.

З доведеної теореми випливають:

Наслідок 1.Якщо і, то.

Наслідок 2.Якщо і c= const, то .

Теорема 3.Відношення нескінченно малої функції α(x)на функцію f(x), межа якої відмінна від нуля, є нескінченно мала функція.

Доведення. Нехай. Тоді 1 /f(x)є обмежена функція. Тому дріб є твір нескінченно малої функції на обмежену функцію, тобто. функція нескінченно мала.

Обчислення нескінченно малих та великих

Обчислення нескінченно малих- обчислення, вироблені з нескінченно малими величинами, у яких похідний результат сприймається як нескінченна сума нескінченно малих. Обчислення нескінченно малих величин є загальним поняттям для диференціальних та інтегральних обчислень, що становлять основу сучасної вищої математики. Поняття нескінченно малої величини тісно пов'язане з поняттям межі.